Skip to content

transforms.scad

Jump to bottom
Revar Desmera edited this page Nov 20, 2024 · 1 revision

LibFile: transforms.scad

Functions and modules that provide shortcuts for translation, rotation and mirror operations. Also provided are skew and frame_map which remaps the coordinate axes. The shortcuts can act on geometry, like the usual OpenSCAD rotate() and translate(). They also work as functions that operate on lists of points in various forms: paths, VNFS and bezier patches. Lastly, the function form of the shortcuts can return a matrix representing the operation the shortcut performs. The rotation and scaling shortcuts accept an optional centerpoint for the rotation or scaling operation.

Almost all of the transformation functions take a point, a point list, bezier patch, or VNF as a second positional argument to operate on. The exceptions are rot(), frame_map() and skew().

To use, add the following lines to the beginning of your file:

include <BOSL2/std.scad>

File Contents

  1. Section: Affine Transformations

  2. Section: Translations

    • move() – Translates children in an arbitrary direction. [Trans] [Path] [VNF] [Mat]
    • left() – Translates children leftwards (X-). [Trans] [Path] [VNF] [Mat]
    • right() – Translates children rightwards (X+). [Trans] [Path] [VNF] [Mat]
    • fwd() – Translates children forwards (Y-). [Trans] [Path] [VNF] [Mat]
    • back() – Translates children backwards (Y+). [Trans] [Path] [VNF] [Mat]
    • down() – Translates children downwards (Z-). [Trans] [Path] [VNF] [Mat]
    • up() – Translates children upwards (Z+). [Trans] [Path] [VNF] [Mat]

  3. Section: Rotations

    • rot() – Rotates children in various ways. [Trans] [Path] [VNF] [Mat]
    • xrot() – Rotates children around the X axis using the right-hand rule. [Trans] [Path] [VNF] [Mat]
    • yrot() – Rotates children around the Y axis using the right-hand rule. [Trans] [Path] [VNF] [Mat]
    • zrot() – Rotates children around the Z axis using the right-hand rule. [Trans] [Path] [VNF] [Mat]
    • tilt() – Tilts children towards a direction [Trans] [Path] [VNF] [Mat]

  4. Section: Scaling

    • scale() – Scales children arbitrarily. [Trans] [Path] [VNF] [Mat] [Ext]
    • xscale() – Scales children along the X axis. [Trans] [Path] [VNF] [Mat]
    • yscale() – Scales children along the Y axis. [Trans] [Path] [VNF] [Mat]
    • zscale() – Scales children along the Z axis. [Trans] [Path] [VNF] [Mat]

  5. Section: Reflection (Mirroring)

    • mirror() – Reflects children across an arbitrary plane. [Trans] [Path] [VNF] [Mat] [Ext]
    • xflip() – Reflects children across the YZ plane. [Trans] [Path] [VNF] [Mat]
    • yflip() – Reflects children across the XZ plane. [Trans] [Path] [VNF] [Mat]
    • zflip() – Reflects children across the XY plane. [Trans] [Path] [VNF] [Mat]

  6. Section: Other Transformations

    • frame_map() – Rotates and possibly skews children from one frame of reference to another. [Trans] [Path] [VNF] [Mat]
    • skew() – Skews children along various axes. [Trans] [Path] [VNF] [Mat]

  7. Section: Applying transformation matrices to data

    • apply() – Applies a transformation matrix to a point, list of points, array of points, or a VNF. [Path] [VNF] [Mat]

Section: Affine Transformations

OpenSCAD provides various built-in modules to transform geometry by translation, scaling, rotation, and mirroring. All of these operations are affine transformations. A three-dimensional affine transformation can be represented by a 4x4 matrix. The transformation shortcuts in this file generally have three modes of operation. They can operate directly on geometry like their OpenSCAD built-in equivalents. For example, left(10) cube(). They can operate on a list of points (or various other types of geometric data). For example, operating on a list of points: points = left(10, [[1,2,3],[4,5,6]]). The third option is that the shortcut can return the transformation matrix corresponding to its action. For example, M=left(10).

This capability allows you to store and manipulate transformations, and can be useful in more advanced modeling. You can multiply these matrices together, analogously to applying a sequence of operations with the built-in transformations. So you can write zrot(37)left(5)cube() to perform two operations on a cube. You can also store that same transformation by multiplying the matrices together: M = zrot(37) * left(5). Note that the order is exactly the same as the order used to apply the transformation.

Suppose you have constructed M as above. What now? You can use the OpensCAD built-in multmatrix to apply it to some geometry: multmatrix(M) cube(). Alternative you can use the BOSL2 function apply to apply M to a point, a list of points, a bezier patch, or a VNF. For example, points = apply(M, [[3,4,5],[5,6,7]]). Note that the apply function can work on both 2D and 3D data, but if you want to operate on 2D data, you must choose transformations that don't modify z

You can use matrices as described above without understanding the details, just treating a matrix as a box that stores a transformation. The OpenSCAD manual section for multmatrix gives some details of how this works. We'll elaborate a bit more below. An affine transformation matrix for three dimensional data is a 4x4 matrix. The top left 3x3 portion gives the linear transformation to apply to the data. For example, it could be a rotation or scaling, or combination of both. The 3x1 column at the top right gives the translation to apply. The bottom row should be [0,0,0,1]. That bottom row is only present to enable the matrices to be multiplied together. OpenSCAD ignores it and in fact multmatrix will accept a 3x4 matrix, where that row is missing. In order for a matrix to act on a point you have to augment the point with an extra 1, making it a length 4 vector. In OpenSCAD you can then compute the the affine transformed point as tran_point = M * point. However, this syntax hides a complication that arises if you have a list of points. A list of points like [[1,2,3,1],[4,5,6,1],[7,8,9,1]] has the augmented points as row vectors on the list. In order to transform such a list, it needs to be muliplied on the right side, not the left side.

Section: Translations

Function/Module: move()

Aliases: translate()

Synopsis: Translates children in an arbitrary direction. [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Translation

See Also: left(), right(), fwd(), back(), down(), up(), spherical_to_xyz(), altaz_to_xyz(), cylindrical_to_xyz(), polar_to_xy()

Usage: As Module

  • move(v) CHILDREN;

Usage: As a function to translate points, VNF, or Bezier patches

  • pts = move(v, p);
  • pts = move(STRING, p);

Usage: Get Translation Matrix

  • mat = move(v);

Description:

Translates position by the given amount.

  • Called as a module, moves/translates all children.
  • Called as a function with the p argument, returns the translated point or list of points.
  • Called as a function with a bezier patch in the p argument, returns the translated patch.
  • Called as a function with a VNF structure in the p argument, returns the translated VNF.
  • Called as a function with the p argument set to a VNF or a polygon and v set to "centroid", "mean" or "box", translates the argument to the centroid, mean, or bounding box center respectively.
  • Called as a function without a p argument, returns a 4x4 translation matrix for operating on 3D data.

Arguments:

By Position What it does
v An [X,Y,Z] vector to translate by. For function form with p a point list or VNF, can be "centroid", "mean" or "box".
p Either a point, or a list of points to be translated when used as a function.

Example 1:

move() Example 1 
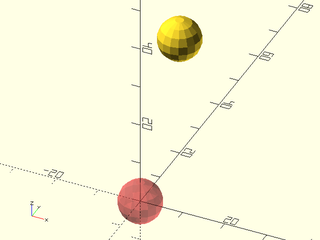
include <BOSL2/std.scad>
#sphere(d=10);
move([0,20,30]) sphere(d=10);



Example 2: You can move a 3D object with a 2D vector. The Z component is treated as zero.

move() Example 2 
include <BOSL2/std.scad>
#sphere(d=10);
move([-10,-5]) sphere(d=10);



Example 3: Move to centroid

move() Example 3 
include <BOSL2/std.scad>
polygon(move("centroid", right_triangle([10,4])));



Example 4: Using Altitude-Azimuth Coordinates

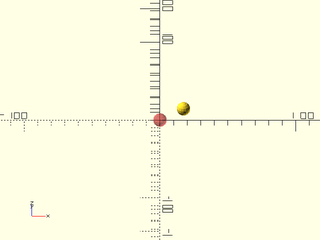
move() Example 4 
include <BOSL2/std.scad>
#sphere(d=10);
move(altaz_to_xyz(30,90,20)) sphere(d=10);



Example 5: Using Spherical Coordinates

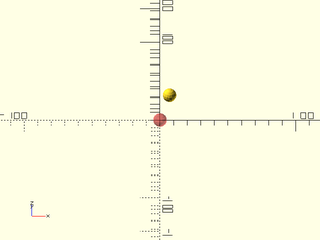
move() Example 5 
include <BOSL2/std.scad>
#sphere(d=10);
move(spherical_to_xyz(20,45,30)) sphere(d=10);



Example 6:

move() Example 6 
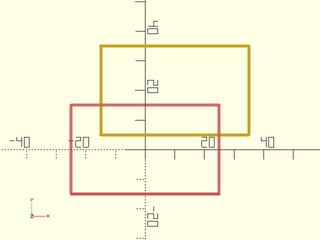
include <BOSL2/std.scad>
path = square([50,30], center=true);
#stroke(path, closed=true);
stroke(move([10,20],p=path), closed=true);



Example 7:

include <BOSL2/std.scad>
pt1 = move([0,20,30], p=[15,23,42]);       // Returns: [15, 43, 72]
pt2 = move([0,3,1], p=[[1,2,3],[4,5,6]]);  // Returns: [[1,5,4], [4,8,7]]
mat2d = move([2,3]);    // Returns: [[1,0,2],[0,1,3],[0,0,1]]
mat3d = move([2,3,4]);  // Returns: [[1,0,0,2],[0,1,0,3],[0,0,1,4],[0,0,0,1]]



Function/Module: left()

Synopsis: Translates children leftwards (X-). [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Translation

See Also: move(), right(), fwd(), back(), down(), up()

Usage: As Module

  • left(x) CHILDREN;

Usage: Translate Points

  • pts = left(x, p);

Usage: Get Translation Matrix

  • mat = left(x);

Description:

If called as a module, moves/translates all children left (in the X- direction) by the given amount. If called as a function with the p argument, returns the translated VNF, point or list of points. If called as a function without the p argument, returns an affine3d translation matrix.

Arguments:

By Position What it does
x Scalar amount to move left.
p Either a point, or a list of points to be translated when used as a function.

Example 1:

left() Example 1 
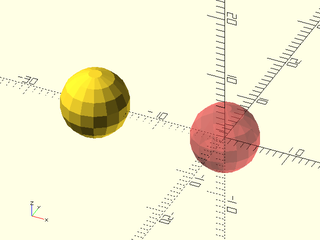
include <BOSL2/std.scad>
#sphere(d=10);
left(20) sphere(d=10);



Example 2:

include <BOSL2/std.scad>
pt1 = left(20, p=[23,42]);           // Returns: [3,42]
pt2 = left(20, p=[15,23,42]);        // Returns: [-5,23,42]
pt3 = left(3, p=[[1,2,3],[4,5,6]]);  // Returns: [[-2,2,3], [1,5,6]]
mat3d = left(4);  // Returns: [[1,0,0,-4],[0,1,0,0],[0,0,1,0],[0,0,0,1]]



Function/Module: right()

Aliases: xmove()

Synopsis: Translates children rightwards (X+). [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Translation

See Also: move(), left(), fwd(), back(), down(), up()

Usage: As Module

  • right(x) CHILDREN;

Usage: Translate Points

  • pts = right(x, p);

Usage: Get Translation Matrix

  • mat = right(x);

Description:

If called as a module, moves/translates all children right (in the X+ direction) by the given amount. If called as a function with the p argument, returns the translated VNF point or list of points. If called as a function without the p argument, returns an affine3d translation matrix.

Arguments:

By Position What it does
x Scalar amount to move right.
p Either a point, or a list of points to be translated when used as a function.

Example 1:

right() Example 1 
include <BOSL2/std.scad>
#sphere(d=10);
right(20) sphere(d=10);



Example 2:

include <BOSL2/std.scad>
pt1 = right(20, p=[23,42]);           // Returns: [43,42]
pt2 = right(20, p=[15,23,42]);        // Returns: [35,23,42]
pt3 = right(3, p=[[1,2,3],[4,5,6]]);  // Returns: [[4,2,3], [7,5,6]]
mat3d = right(4);  // Returns: [[1,0,0,4],[0,1,0,0],[0,0,1,0],[0,0,0,1]]



Function/Module: fwd()

Synopsis: Translates children forwards (Y-). [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Translation

See Also: move(), left(), right(), back(), down(), up()

Usage: As Module

  • fwd(y) CHILDREN;

Usage: Translate Points

  • pts = fwd(y, p);

Usage: Get Translation Matrix

  • mat = fwd(y);

Description:

If called as a module, moves/translates all children forward (in the Y- direction) by the given amount. If called as a function with the p argument, returns the translated VNF, point or list of points. If called as a function without the p argument, returns an affine3d translation matrix.

Arguments:

By Position What it does
y Scalar amount to move forward.
p Either a point, or a list of points to be translated when used as a function.

Example 1:

fwd() Example 1 
include <BOSL2/std.scad>
#sphere(d=10);
fwd(20) sphere(d=10);



Example 2:

include <BOSL2/std.scad>
pt1 = fwd(20, p=[23,42]);           // Returns: [23,22]
pt2 = fwd(20, p=[15,23,42]);        // Returns: [15,3,42]
pt3 = fwd(3, p=[[1,2,3],[4,5,6]]);  // Returns: [[1,-1,3], [4,2,6]]
mat3d = fwd(4);  // Returns: [[1,0,0,0],[0,1,0,-4],[0,0,1,0],[0,0,0,1]]



Function/Module: back()

Aliases: ymove()

Synopsis: Translates children backwards (Y+). [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Translation

See Also: move(), left(), right(), fwd(), down(), up()

Usage: As Module

  • back(y) CHILDREN;

Usage: Translate Points

  • pts = back(y, p);

Usage: Get Translation Matrix

  • mat = back(y);

Description:

If called as a module, moves/translates all children back (in the Y+ direction) by the given amount. If called as a function with the p argument, returns the translated VNF, point or list of points. If called as a function without the p argument, returns an affine3d translation matrix.

Arguments:

By Position What it does
y Scalar amount to move back.
p Either a point, or a list of points to be translated when used as a function.

Example 1:

back() Example 1 
include <BOSL2/std.scad>
#sphere(d=10);
back(20) sphere(d=10);



Example 2:

include <BOSL2/std.scad>
pt1 = back(20, p=[23,42]);           // Returns: [23,62]
pt2 = back(20, p=[15,23,42]);        // Returns: [15,43,42]
pt3 = back(3, p=[[1,2,3],[4,5,6]]);  // Returns: [[1,5,3], [4,8,6]]
mat3d = back(4);  // Returns: [[1,0,0,0],[0,1,0,4],[0,0,1,0],[0,0,0,1]]



Function/Module: down()

Synopsis: Translates children downwards (Z-). [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Translation

See Also: move(), left(), right(), fwd(), back(), up()

Usage: As Module

  • down(z) CHILDREN;

Usage: Translate Points

  • pts = down(z, p);

Usage: Get Translation Matrix

  • mat = down(z);

Description:

If called as a module, moves/translates all children down (in the Z- direction) by the given amount. If called as a function with the p argument, returns the translated VNF, point or list of points. If called as a function without the p argument, returns an affine3d translation matrix.

Arguments:

By Position What it does
z Scalar amount to move down.
p Either a point, or a list of points to be translated when used as a function.

Example 1:

down() Example 1 
include <BOSL2/std.scad>
#sphere(d=10);
down(20) sphere(d=10);



Example 2:

include <BOSL2/std.scad>
pt1 = down(20, p=[15,23,42]);        // Returns: [15,23,22]
pt2 = down(3, p=[[1,2,3],[4,5,6]]);  // Returns: [[1,2,0], [4,5,3]]
mat3d = down(4);  // Returns: [[1,0,0,0],[0,1,0,0],[0,0,1,-4],[0,0,0,1]]



Function/Module: up()

Aliases: zmove()

Synopsis: Translates children upwards (Z+). [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Translation

See Also: move(), left(), right(), fwd(), back(), down()

Usage: As Module

  • up(z) CHILDREN;

Usage: Translate Points

  • pts = up(z, p);

Usage: Get Translation Matrix

  • mat = up(z);

Description:

If called as a module, moves/translates all children up (in the Z+ direction) by the given amount. If called as a function with the p argument, returns the translated VNF, point or list of points. If called as a function without the p argument, returns an affine3d translation matrix.

Arguments:

By Position What it does
z Scalar amount to move up.
p Either a point, or a list of points to be translated when used as a function.

Example 1:

up() Example 1 
include <BOSL2/std.scad>
#sphere(d=10);
up(20) sphere(d=10);



Example 2:

include <BOSL2/std.scad>
pt1 = up(20, p=[15,23,42]);        // Returns: [15,23,62]
pt2 = up(3, p=[[1,2,3],[4,5,6]]);  // Returns: [[1,2,6], [4,5,9]]
mat3d = up(4);  // Returns: [[1,0,0,0],[0,1,0,0],[0,0,1,4],[0,0,0,1]]



Section: Rotations

Function/Module: rot()

Synopsis: Rotates children in various ways. [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Rotation

See Also: xrot(), yrot(), zrot(), tilt()

Usage: As a Module

  • rot(a, [cp=], [reverse=]) CHILDREN;
  • rot([X,Y,Z], [cp=], [reverse=]) CHILDREN;
  • rot(a, v, [cp=], [reverse=]) CHILDREN;
  • rot(from=, to=, [a=], [reverse=]) CHILDREN;

Usage: As a Function to transform data in p

  • pts = rot(a, p=, [cp=], [reverse=]);
  • pts = rot([X,Y,Z], p=, [cp=], [reverse=]);
  • pts = rot(a, v, p=, [cp=], [reverse=]);
  • pts = rot([a], from=, to=, p=, [reverse=]);

Usage: As a Function to return a transform matrix

  • M = rot(a, [cp=], [reverse=]);
  • M = rot([X,Y,Z], [cp=], [reverse=]);
  • M = rot(a, v, [cp=], [reverse=]);
  • M = rot(from=, to=, [a=], [reverse=]);

Description:

This is a shorthand version of the built-in rotate(), and operates similarly, with a few additional capabilities. You can specify the rotation to perform in one of several ways:

  • rot(30) or rot(a=30) rotates 30 degrees around the Z axis.
  • rot([20,30,40]) or rot(a=[20,30,40]) rotates 20 degrees around the X axis, then 30 degrees around the Y axis, then 40 degrees around the Z axis.
  • rot(30, [1,1,0]) or rot(a=30, v=[1,1,0]) rotates 30 degrees around the axis vector [1,1,0].
  • rot(from=[0,0,1], to=[1,0,0]) rotates the from vector to line up with the to vector, in this case the top to the right and hence equivalent to rot(a=90,v=[0,1,0].
  • rot(from=[0,1,1], to=[1,1,0], a=45) rotates 45 degrees around the from vector ([0,1,1]) and then rotates the from vector to align with the to vector. Equivalent to rot(from=[0,1,1],to=[1,1,0]) rot(a=45,v=[0,1,1]). You can also regard a as as post-rotation around the to vector. For this form, a must be a scalar.
  • If the cp centerpoint argument is given, then rotations are performed around that centerpoint. So rot(args...,cp=[1,2,3]) is equivalent to move(-[1,2,3])rot(args...)move([1,2,3]).
  • If the reverse argument is true, then the rotations performed will be exactly reversed.

The behavior and return value varies depending on how rot() is called:

  • Called as a module, rotates all children.
  • Called as a function with a p argument containing a point, returns the rotated point.
  • Called as a function with a p argument containing a list of points, returns the list of rotated points.
  • Called as a function with a bezier patch in the p argument, returns the rotated patch.
  • Called as a function with a VNF structure in the p argument, returns the rotated VNF.
  • Called as a function without a p argument, returns the affine3d rotational matrix. Note that unlike almost all the other transformations, the p argument must be given as a named argument.

Arguments:

By Position What it does
a Scalar angle or vector of XYZ rotation angles to rotate by, in degrees. If you use the from and to arguments then a must be a scalar. Default: 0
v vector for the axis of rotation. Default: [0,0,1] or UP
By Name What it does
cp centerpoint to rotate around. Default: [0,0,0]
from Starting vector for vector-based rotations.
to Target vector for vector-based rotations.
reverse If true, exactly reverses the rotation, including axis rotation ordering. Default: false
p If called as a function, this contains data to rotate: a point, list of points, bezier patch or VNF.

Example 1:

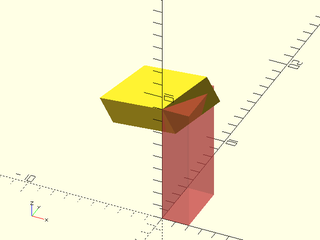
rot() Example 1 
include <BOSL2/std.scad>
#cube([2,4,9]);
rot([30,60,0], cp=[0,0,9]) cube([2,4,9]);



Example 2:

rot() Example 2 
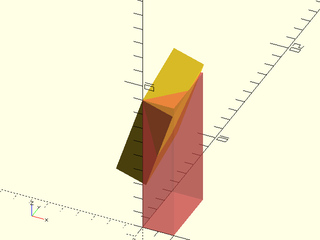
include <BOSL2/std.scad>
#cube([2,4,9]);
rot(30, v=[1,1,0], cp=[0,0,9]) cube([2,4,9]);



Example 3:

rot() Example 3 
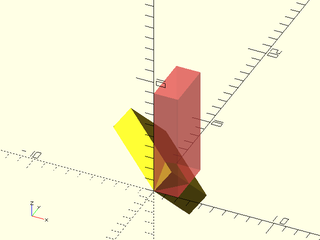
include <BOSL2/std.scad>
#cube([2,4,9]);
rot(from=UP, to=LEFT+BACK) cube([2,4,9]);



Example 4:

rot() Example 4 
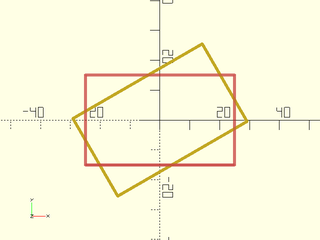
include <BOSL2/std.scad>
path = square([50,30], center=true);
#stroke(path, closed=true);
stroke(rot(30,p=path), closed=true);



Function/Module: xrot()

Synopsis: Rotates children around the X axis using the right-hand rule. [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Rotation

See Also: rot(), yrot(), zrot(), tilt()

Usage: As Module

  • xrot(a, [cp=]) CHILDREN;

Usage: As a function to rotate points

  • rotated = xrot(a, p, [cp=]);

Usage: As a function to return rotation matrix

  • mat = xrot(a, [cp=]);

Description:

Rotates around the X axis by the given number of degrees. If cp is given, rotations are performed around that centerpoint.

  • Called as a module, rotates all children.
  • Called as a function with a p argument containing a point, returns the rotated point.
  • Called as a function with a p argument containing a list of points, returns the list of rotated points.
  • Called as a function with a bezier patch in the p argument, returns the rotated patch.
  • Called as a function with a VNF structure in the p argument, returns the rotated VNF.
  • Called as a function without a p argument, returns the affine3d rotational matrix.

Arguments:

By Position What it does
a angle to rotate by in degrees.
p If called as a function, this contains data to rotate: a point, list of points, bezier patch or VNF.
By Name What it does
cp centerpoint to rotate around. Default: [0,0,0]

Example 1:

xrot() Example 1 
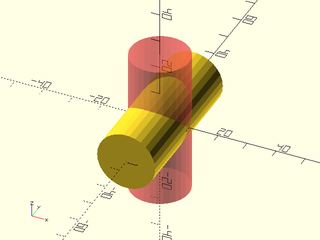
include <BOSL2/std.scad>
#cylinder(h=50, r=10, center=true);
xrot(90) cylinder(h=50, r=10, center=true);



Function/Module: yrot()

Synopsis: Rotates children around the Y axis using the right-hand rule. [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Rotation

See Also: rot(), xrot(), zrot(), tilt()

Usage: As Module

  • yrot(a, [cp=]) CHILDREN;

Usage: Rotate Points

  • rotated = yrot(a, p, [cp=]);

Usage: Get Rotation Matrix

  • mat = yrot(a, [cp=]);

Description:

Rotates around the Y axis by the given number of degrees. If cp is given, rotations are performed around that centerpoint.

  • Called as a module, rotates all children.
  • Called as a function with a p argument containing a point, returns the rotated point.
  • Called as a function with a p argument containing a list of points, returns the list of rotated points.
  • Called as a function with a bezier patch in the p argument, returns the rotated patch.
  • Called as a function with a VNF structure in the p argument, returns the rotated VNF.
  • Called as a function without a p argument, returns the affine3d rotational matrix.

Arguments:

By Position What it does
a angle to rotate by in degrees.
p If called as a function, this contains data to rotate: a point, list of points, bezier patch or VNF.
By Name What it does
cp centerpoint to rotate around. Default: [0,0,0]

Example 1:

yrot() Example 1 
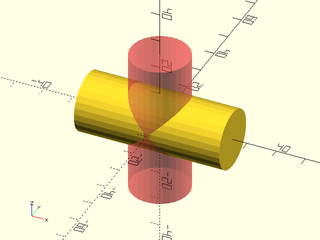
include <BOSL2/std.scad>
#cylinder(h=50, r=10, center=true);
yrot(90) cylinder(h=50, r=10, center=true);



Function/Module: zrot()

Synopsis: Rotates children around the Z axis using the right-hand rule. [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Rotation

See Also: rot(), xrot(), yrot(), tilt()

Usage: As Module

  • zrot(a, [cp=]) CHILDREN;

Usage: As Function to rotate points

  • rotated = zrot(a, p, [cp=]);

Usage: As Function to return rotation matrix

  • mat = zrot(a, [cp=]);

Description:

Rotates around the Z axis by the given number of degrees. If cp is given, rotations are performed around that centerpoint.

  • Called as a module, rotates all children.
  • Called as a function with a p argument containing a point, returns the rotated point.
  • Called as a function with a p argument containing a list of points, returns the list of rotated points.
  • Called as a function with a bezier patch in the p argument, returns the rotated patch.
  • Called as a function with a VNF structure in the p argument, returns the rotated VNF.
  • Called as a function without a p argument, returns the affine3d rotational matrix.

Arguments:

By Position What it does
a angle to rotate by in degrees.
p If called as a function, this contains data to rotate: a point, list of points, bezier patch or VNF.
By Name What it does
cp centerpoint to rotate around. Default: [0,0,0]

Example 1:

zrot() Example 1 
include <BOSL2/std.scad>
#cube(size=[60,20,40], center=true);
zrot(90) cube(size=[60,20,40], center=true);



Function/Module: tilt()

Synopsis: Tilts children towards a direction [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Rotation

See Also: rot(), xrot(), yrot(), zrot()

Usage: As a Module

  • tilt(to=, [reverse=], [cp=]) CHILDREN;

Usage: As a Function to transform data in p

  • pts = tilt(to=, p=, [reverse=], [cp=]);

Usage: As a Function to return a transform matrix

  • M = tilt(to=, [reverse=], [cp=]);

Description:

This is shorthand for rot(from=UP,to=x) and operates similarly. It tilts that which is pointing UP until it is pointing at the given direction vector.

  • If the cp centerpoint argument is given, then the tilt/rotation is performed around that centerpoint. So tilt(...,cp=[1,2,3]) is equivalent to move([1,2,3]) tilt(...) move([-1,-2,-3]).
  • If the reverse argument is true, then the tilt/rotation performed will be exactly reversed.

The behavior and return value varies depending on how tilt() is called:

  • Called as a module, tilts all children.
  • Called as a function with a p argument containing a point, returns the tilted/rotated point.
  • Called as a function with a p argument containing a list of points, returns the list of tilted/rotated points.
  • Called as a function with a bezier patch in the p argument, returns the tilted/rotated patch.
  • Called as a function with a VNF structure in the p argument, returns the tilted/rotated VNF.
  • Called as a function without a p argument, returns the affine3d rotational matrix. Note that unlike almost all the other transformations, the p argument must be given as a named argument.

Arguments:

By Position What it does
to Target vector for vector-based rotations.
By Name What it does
cp centerpoint to tilt/rotate around. Default: [0,0,0]
reverse If true, exactly reverses the rotation. Default: false
p If called as a function, this contains data to rotate: a point, list of points, bezier patch or a VNF.

Example 1:

tilt() Example 1 
include <BOSL2/std.scad>
#cube([2,4,9]);
tilt(LEFT+BACK) cube([2,4,9]);



Example 2:

tilt() Example 2 
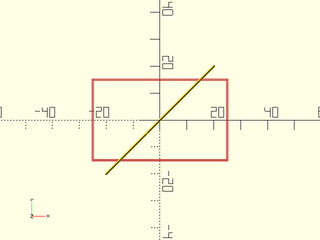
include <BOSL2/std.scad>
path = square([50,30], center=true);
#stroke(path, closed=true);
stroke(tilt(RIGHT+FWD,p=path3d(path)), closed=true);



Section: Scaling

Function/Module: scale()

Synopsis: Scales children arbitrarily. [Trans] [Path] [VNF] [Mat] [Ext]

Topics: Affine, Matrices, Transforms, Scaling

See Also: xscale(), yscale(), zscale()

Usage: As Module

  • scale(SCALAR) CHILDREN;
  • scale([X,Y,Z]) CHILDREN;

Usage: Scale Points

  • pts = scale(v, p, [cp=]);

Usage: Get Scaling Matrix

  • mat = scale(v, [cp=]);

Description:

Scales by the [X,Y,Z] scaling factors given in v. If v is given as a scalar number, all axes are scaled uniformly by that amount.

  • Called as the built-in module, scales all children.
  • Called as a function with a point in the p argument, returns the scaled point.
  • Called as a function with a list of points in the p argument, returns the list of scaled points.
  • Called as a function with a bezier patch in the p argument, returns the scaled patch.
  • Called as a function with a VNF structure in the p argument, returns the scaled VNF.
  • Called as a function without a p argument, and a 2D list of scaling factors in v, returns an affine2d scaling matrix.
  • Called as a function without a p argument, and a 3D list of scaling factors in v, returns an affine3d scaling matrix.

Arguments:

By Position What it does
v Either a numeric uniform scaling factor, or a list of [X,Y,Z] scaling factors. Default: 1
p If called as a function, the point or list of points to scale.
By Name What it does
cp If given, centers the scaling on the point cp.

Example 1:

include <BOSL2/std.scad>
pt1 = scale(3, p=[3,1,4]);        // Returns: [9,3,12]
pt2 = scale([2,3,4], p=[3,1,4]);  // Returns: [6,3,16]
pt3 = scale([2,3,4], p=[[1,2,3],[4,5,6]]);  // Returns: [[2,6,12], [8,15,24]]
mat2d = scale([2,3]);    // Returns: [[2,0,0],[0,3,0],[0,0,1]]
mat3d = scale([2,3,4]);  // Returns: [[2,0,0,0],[0,3,0,0],[0,0,4,0],[0,0,0,1]]



Example 2:

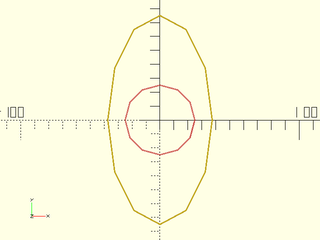
scale() Example 2 
include <BOSL2/std.scad>
path = circle(d=50,$fn=12);
#stroke(path,closed=true);
stroke(scale([1.5,3],p=path),closed=true);



Function/Module: xscale()

Synopsis: Scales children along the X axis. [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Scaling

See Also: scale(), yscale(), zscale()

Usage: As Module

  • xscale(x, [cp=]) CHILDREN;

Usage: Scale Points

  • scaled = xscale(x, p, [cp=]);

Usage: Get Affine Matrix

  • mat = xscale(x, [cp=]);

Description:

Scales along the X axis by the scaling factor x.

  • Called as the built-in module, scales all children.
  • Called as a function with a point in the p argument, returns the scaled point.
  • Called as a function with a list of points in the p argument, returns the list of scaled points.
  • Called as a function with a bezier patch in the p argument, returns the scaled patch.
  • Called as a function with a VNF structure in the p argument, returns the scaled VNF.
  • Called as a function without a p argument, and a 2D list of scaling factors in v, returns an affine2d scaling matrix.
  • Called as a function without a p argument, and a 3D list of scaling factors in v, returns an affine3d scaling matrix.

Arguments:

By Position What it does
x Factor to scale by, along the X axis.
p A point, path, bezier patch, or VNF to scale, when called as a function.
By Name What it does
cp If given as a point, centers the scaling on the point cp. If given as a scalar, centers scaling on the point [cp,0,0]

Example 1: As Module

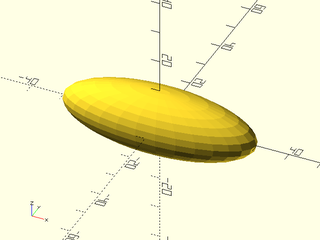
xscale() Example 1 
include <BOSL2/std.scad>
xscale(3) sphere(r=10);



Example 2: Scaling Points

xscale() Example 2 
include <BOSL2/std.scad>
path = circle(d=50,$fn=12);
#stroke(path,closed=true);
stroke(xscale(2,p=path),closed=true);



Function/Module: yscale()

Synopsis: Scales children along the Y axis. [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Scaling

See Also: scale(), xscale(), zscale()

Usage: As Module

  • yscale(y, [cp=]) CHILDREN;

Usage: Scale Points

  • scaled = yscale(y, p, [cp=]);

Usage: Get Affine Matrix

  • mat = yscale(y, [cp=]);

Description:

Scales along the Y axis by the scaling factor y.

  • Called as the built-in module, scales all children.
  • Called as a function with a point in the p argument, returns the scaled point.
  • Called as a function with a list of points in the p argument, returns the list of scaled points.
  • Called as a function with a bezier patch in the p argument, returns the scaled patch.
  • Called as a function with a VNF structure in the p argument, returns the scaled VNF.
  • Called as a function without a p argument, and a 2D list of scaling factors in v, returns an affine2d scaling matrix.
  • Called as a function without a p argument, and a 3D list of scaling factors in v, returns an affine3d scaling matrix.

Arguments:

By Position What it does
y Factor to scale by, along the Y axis.
p A point, path, bezier patch, or VNF to scale, when called as a function.
By Name What it does
cp If given as a point, centers the scaling on the point cp. If given as a scalar, centers scaling on the point [0,cp,0]

Example 1: As Module

yscale() Example 1 
include <BOSL2/std.scad>
yscale(3) sphere(r=10);



Example 2: Scaling Points

yscale() Example 2 
include <BOSL2/std.scad>
path = circle(d=50,$fn=12);
#stroke(path,closed=true);
stroke(yscale(2,p=path),closed=true);



Function/Module: zscale()

Synopsis: Scales children along the Z axis. [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Scaling

See Also: scale(), xscale(), yscale()

Usage: As Module

  • zscale(z, [cp=]) CHILDREN;

Usage: Scale Points

  • scaled = zscale(z, p, [cp=]);

Usage: Get Affine Matrix

  • mat = zscale(z, [cp=]);

Description:

Scales along the Z axis by the scaling factor z.

  • Called as the built-in module, scales all children.
  • Called as a function with a point in the p argument, returns the scaled point.
  • Called as a function with a list of points in the p argument, returns the list of scaled points.
  • Called as a function with a bezier patch in the p argument, returns the scaled patch.
  • Called as a function with a VNF structure in the p argument, returns the scaled VNF.
  • Called as a function without a p argument, and a 2D list of scaling factors in v, returns an affine2d scaling matrix.
  • Called as a function without a p argument, and a 3D list of scaling factors in v, returns an affine3d scaling matrix.

Arguments:

By Position What it does
z Factor to scale by, along the Z axis.
p A point, path, bezier patch, or VNF to scale, when called as a function.
By Name What it does
cp If given as a point, centers the scaling on the point cp. If given as a scalar, centers scaling on the point [0,0,cp]

Example 1: As Module

zscale() Example 1 
include <BOSL2/std.scad>
zscale(3) sphere(r=10);



Example 2: Scaling Points

zscale() Example 2 
include <BOSL2/std.scad>
path = xrot(90,p=path3d(circle(d=50,$fn=12)));
#stroke(path,closed=true);
stroke(zscale(2,path),closed=true);



Section: Reflection (Mirroring)

Function/Module: mirror()

Synopsis: Reflects children across an arbitrary plane. [Trans] [Path] [VNF] [Mat] [Ext]

Topics: Affine, Matrices, Transforms, Reflection, Mirroring

See Also: xflip(), yflip(), zflip()

Usage: As Module

  • mirror(v) CHILDREN;

Usage: As Function

  • pt = mirror(v, p);

Usage: Get Reflection/Mirror Matrix

  • mat = mirror(v);

Description:

Mirrors/reflects across the plane or line whose normal vector is given in v.

  • Called as the built-in module, mirrors all children across the line/plane.
  • Called as a function with a point in the p argument, returns the point mirrored across the line/plane.
  • Called as a function with a list of points in the p argument, returns the list of points, with each one mirrored across the line/plane.
  • Called as a function with a bezier patch in the p argument, returns the mirrored patch.
  • Called as a function with a VNF structure in the p argument, returns the mirrored VNF.
  • Called as a function without a p argument, and with a 2D normal vector v, returns the affine2d 3x3 mirror matrix.
  • Called as a function without a p argument, and with a 3D normal vector v, returns the affine3d 4x4 mirror matrix.

Arguments:

By Position What it does
v The normal vector of the line or plane to mirror across.
p If called as a function, the point or list of points to scale.

Example 1:

mirror() Example 1 
include <BOSL2/std.scad>
n = [1,0,0];
module obj() right(20) rotate([0,15,-15]) cube([40,30,20]);
obj();
mirror(n) obj();
rot(a=atan2(n.y,n.x),from=UP,to=n) {
    color("red") anchor_arrow(s=20, flag=false);
    color("#7777") cube([75,75,0.1], center=true);
}



Example 2:

mirror() Example 2 
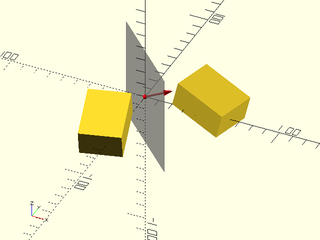
include <BOSL2/std.scad>
n = [1,1,0];
module obj() right(20) rotate([0,15,-15]) cube([40,30,20]);
obj();
mirror(n) obj();
rot(a=atan2(n.y,n.x),from=UP,to=n) {
    color("red") anchor_arrow(s=20, flag=false);
    color("#7777") cube([75,75,0.1], center=true);
}



Example 3:

mirror() Example 3 
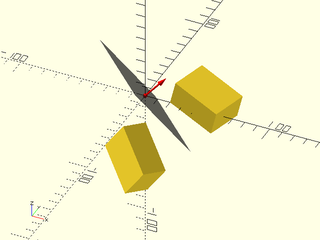
include <BOSL2/std.scad>
n = [1,1,1];
module obj() right(20) rotate([0,15,-15]) cube([40,30,20]);
obj();
mirror(n) obj();
rot(a=atan2(n.y,n.x),from=UP,to=n) {
    color("red") anchor_arrow(s=20, flag=false);
    color("#7777") cube([75,75,0.1], center=true);
}



Example 4:

mirror() Example 4 
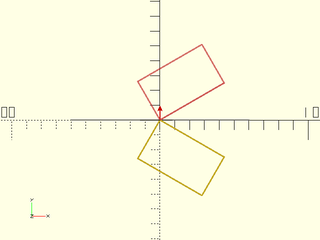
include <BOSL2/std.scad>
n = [0,1];
path = rot(30, p=square([50,30]));
color("gray") rot(from=[0,1],to=n) stroke([[-60,0],[60,0]]);
color("red") stroke([[0,0],10*n],endcap2="arrow2");
#stroke(path,closed=true);
stroke(mirror(n, p=path),closed=true);



Example 5:

mirror() Example 5 
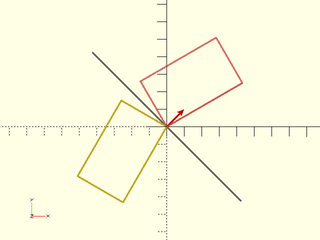
include <BOSL2/std.scad>
n = [1,1];
path = rot(30, p=square([50,30]));
color("gray") rot(from=[0,1],to=n) stroke([[-60,0],[60,0]]);
color("red") stroke([[0,0],10*n],endcap2="arrow2");
#stroke(path,closed=true);
stroke(mirror(n, p=path),closed=true);



Function/Module: xflip()

Synopsis: Reflects children across the YZ plane. [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Reflection, Mirroring

See Also: mirror(), yflip(), zflip()

Usage: As Module

  • xflip([x=]) CHILDREN;

Usage: As Function

  • pt = xflip(p, [x]);

Usage: Get Affine Matrix

  • mat = xflip([x=]);

Description:

Mirrors/reflects across the origin [0,0,0], along the X axis. If x is given, reflects across [x,0,0] instead.

  • Called as the built-in module, mirrors all children across the line/plane.
  • Called as a function with a point in the p argument, returns the point mirrored across the line/plane.
  • Called as a function with a list of points in the p argument, returns the list of points, with each one mirrored across the line/plane.
  • Called as a function with a bezier patch in the p argument, returns the mirrored patch.
  • Called as a function with a VNF structure in the p argument, returns the mirrored VNF.
  • Called as a function without a p argument, returns the affine3d 4x4 mirror matrix.

Arguments:

By Position What it does
p If given, the point, path, patch, or VNF to mirror. Function use only.
x The X coordinate of the plane of reflection. Default: 0

Example 1:

xflip() Example 1 
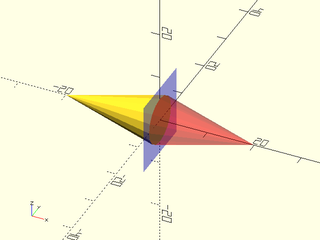
include <BOSL2/std.scad>
xflip() yrot(90) cylinder(d1=10, d2=0, h=20);
color("blue", 0.25) cube([0.01,15,15], center=true);
color("red", 0.333) yrot(90) cylinder(d1=10, d2=0, h=20);



Example 2:

xflip() Example 2 
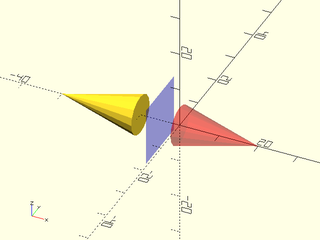
include <BOSL2/std.scad>
xflip(x=-5) yrot(90) cylinder(d1=10, d2=0, h=20);
color("blue", 0.25) left(5) cube([0.01,15,15], center=true);
color("red", 0.333) yrot(90) cylinder(d1=10, d2=0, h=20);



Function/Module: yflip()

Synopsis: Reflects children across the XZ plane. [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Reflection, Mirroring

See Also: mirror(), xflip(), zflip()

Usage: As Module

  • yflip([y=]) CHILDREN;

Usage: As Function

  • pt = yflip(p, [y]);

Usage: Get Affine Matrix

  • mat = yflip([y=]);

Description:

Mirrors/reflects across the origin [0,0,0], along the Y axis. If y is given, reflects across [0,y,0] instead.

  • Called as the built-in module, mirrors all children across the line/plane.
  • Called as a function with a point in the p argument, returns the point mirrored across the line/plane.
  • Called as a function with a list of points in the p argument, returns the list of points, with each one mirrored across the line/plane.
  • Called as a function with a bezier patch in the p argument, returns the mirrored patch.
  • Called as a function with a VNF structure in the p argument, returns the mirrored VNF.
  • Called as a function without a p argument, returns the affine3d 4x4 mirror matrix.

Arguments:

By Position What it does
p If given, the point, path, patch, or VNF to mirror. Function use only.
y The Y coordinate of the plane of reflection. Default: 0

Example 1:

yflip() Example 1 
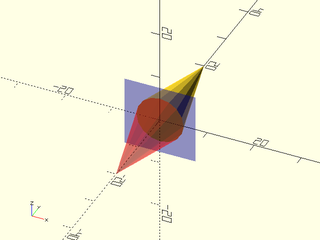
include <BOSL2/std.scad>
yflip() xrot(90) cylinder(d1=10, d2=0, h=20);
color("blue", 0.25) cube([15,0.01,15], center=true);
color("red", 0.333) xrot(90) cylinder(d1=10, d2=0, h=20);



Example 2:

yflip() Example 2 
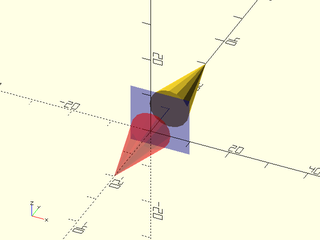
include <BOSL2/std.scad>
yflip(y=5) xrot(90) cylinder(d1=10, d2=0, h=20);
color("blue", 0.25) back(5) cube([15,0.01,15], center=true);
color("red", 0.333) xrot(90) cylinder(d1=10, d2=0, h=20);



Function/Module: zflip()

Synopsis: Reflects children across the XY plane. [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Reflection, Mirroring

See Also: mirror(), xflip(), yflip()

Usage: As Module

  • zflip([z=]) CHILDREN;

Usage: As Function

  • pt = zflip(p, [z]);

Usage: Get Affine Matrix

  • mat = zflip([z=]);

Description:

Mirrors/reflects across the origin [0,0,0], along the Z axis. If z is given, reflects across [0,0,z] instead.

  • Called as the built-in module, mirrors all children across the line/plane.
  • Called as a function with a point in the p argument, returns the point mirrored across the line/plane.
  • Called as a function with a list of points in the p argument, returns the list of points, with each one mirrored across the line/plane.
  • Called as a function with a bezier patch in the p argument, returns the mirrored patch.
  • Called as a function with a VNF structure in the p argument, returns the mirrored VNF.
  • Called as a function without a p argument, returns the affine3d 4x4 mirror matrix.

Arguments:

By Position What it does
p If given, the point, path, patch, or VNF to mirror. Function use only.
z The Z coordinate of the plane of reflection. Default: 0

Example 1:

zflip() Example 1 
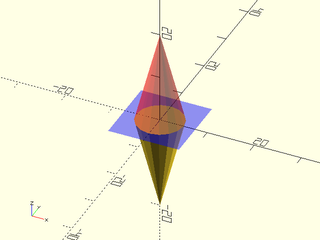
include <BOSL2/std.scad>
zflip() cylinder(d1=10, d2=0, h=20);
color("blue", 0.25) cube([15,15,0.01], center=true);
color("red", 0.333) cylinder(d1=10, d2=0, h=20);



Example 2:

zflip() Example 2 
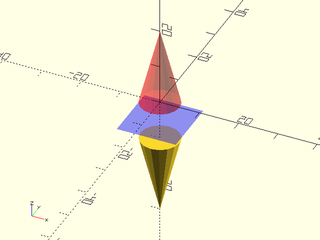
include <BOSL2/std.scad>
zflip(z=-5) cylinder(d1=10, d2=0, h=20);
color("blue", 0.25) down(5) cube([15,15,0.01], center=true);
color("red", 0.333) cylinder(d1=10, d2=0, h=20);



Section: Other Transformations

Function/Module: frame_map()

Synopsis: Rotates and possibly skews children from one frame of reference to another. [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Rotation

See Also: rot(), xrot(), yrot(), zrot()

Usage: As module

  • frame_map(v1, v2, v3, [reverse=]) CHILDREN;

Usage: As function to remap points

  • transformed = frame_map(v1, v2, v3, p=points, [reverse=]);

Usage: As function to return a transformation matrix:

  • map = frame_map(v1, v2, v3, [reverse=]);
  • map = frame_map(x=VECTOR1, y=VECTOR2, [reverse=]);
  • map = frame_map(x=VECTOR1, z=VECTOR2, [reverse=]);
  • map = frame_map(y=VECTOR1, z=VECTOR2, [reverse=]);

Description:

Maps one coordinate frame to another. You must specify two or three of x, y, and z. The specified axes are mapped to the vectors you supplied, so if you specify x=[1,1] then the x axis will be mapped to the line y=x. If you give two inputs, the third vector is mapped to the appropriate normal to maintain a right hand coordinate system. If the vectors you give are orthogonal the result will be a rotation and the reverse parameter will supply the inverse map, which enables you to map two arbitrary coordinate systems to each other by using the canonical coordinate system as an intermediary. You cannot use the reverse option with non-orthogonal inputs. Note that only the direction of the specified vectors matters: the transformation will not apply scaling, though it can skew if your provide non-orthogonal axes.

Arguments:

By Position What it does
x Destination 3D vector for x axis.
y Destination 3D vector for y axis.
z Destination 3D vector for z axis.
p If given, the point, path, patch, or VNF to operate on. Function use only.
reverse reverse direction of the map for orthogonal inputs. Default: false

Example 1: Remap axes after linear extrusion

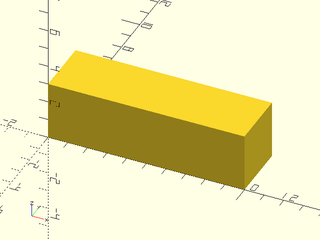
frame\_map() Example 1 
include <BOSL2/std.scad>
frame_map(x=[0,1,0], y=[0,0,1]) linear_extrude(height=10) square(3);

Example 2: This map is just a rotation around the z axis

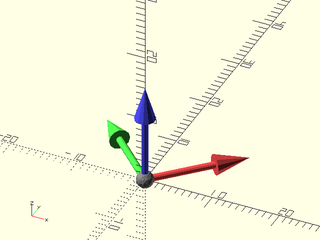
frame\_map() Example 2 
include <BOSL2/std.scad>
mat = frame_map(x=[1,1,0], y=[-1,1,0]);
multmatrix(mat) frame_ref();



Example 3: This map is not a rotation because x and y aren't orthogonal

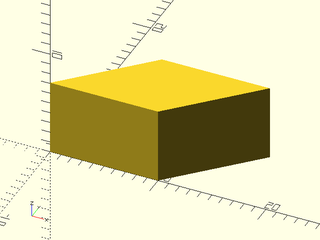
frame\_map() Example 3 
include <BOSL2/std.scad>
frame_map(x=[1,0,0], y=[1,1,0]) cube(10);



Example 4: This sends [1,1,0] to [0,1,1] and [-1,1,0] to [0,-1,1]. (Original directions shown in light shade, final directions shown dark.)

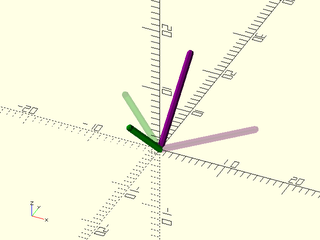
frame\_map() Example 4 
include <BOSL2/std.scad>
mat = frame_map(x=[0,1,1], y=[0,-1,1]) * frame_map(x=[1,1,0], y=[-1,1,0],reverse=true);
color("purple",alpha=.2) stroke([[0,0,0],10*[1,1,0]]);
color("green",alpha=.2)  stroke([[0,0,0],10*[-1,1,0]]);
multmatrix(mat) {
   color("purple") stroke([[0,0,0],10*[1,1,0]]);
   color("green") stroke([[0,0,0],10*[-1,1,0]]);
}

Function/Module: skew()

Synopsis: Skews children along various axes. [Trans] [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms, Skewing

See Also: move(), rot(), scale()

Usage: As Module

  • skew([sxy=]|[axy=], [sxz=]|[axz=], [syx=]|[ayx=], [syz=]|[ayz=], [szx=]|[azx=], [szy=]|[azy=]) CHILDREN;

Usage: As Function

  • pts = skew(p, [sxy=]|[axy=], [sxz=]|[axz=], [syx=]|[ayx=], [syz=]|[ayz=], [szx=]|[azx=], [szy=]|[azy=]);

Usage: Get Affine Matrix

  • mat = skew([sxy=]|[axy=], [sxz=]|[axz=], [syx=]|[ayx=], [syz=]|[ayz=], [szx=]|[azx=], [szy=]|[azy=]);

Description:

Skews geometry by the given skew factors.

  • Called as the built-in module, skews all children.
  • Called as a function with a point in the p argument, returns the skewed point.
  • Called as a function with a list of points in the p argument, returns the list of skewed points.
  • Called as a function with a bezier patch in the p argument, returns the skewed patch.
  • Called as a function with a VNF structure in the p argument, returns the skewed VNF.
  • Called as a function without a p argument, returns the affine3d 4x4 skew matrix. Each skew factor is a multiplier. For example, if sxy=2, then it will skew along the X axis by 2x the value of the Y axis.

Arguments:

By Position What it does
p If given, the point, path, patch, or VNF to skew. Function use only.
By Name What it does
sxy Skew factor multiplier for skewing along the X axis as you get farther from the Y axis. Default: 0
sxz Skew factor multiplier for skewing along the X axis as you get farther from the Z axis. Default: 0
syx Skew factor multiplier for skewing along the Y axis as you get farther from the X axis. Default: 0
syz Skew factor multiplier for skewing along the Y axis as you get farther from the Z axis. Default: 0
szx Skew factor multiplier for skewing along the Z axis as you get farther from the X axis. Default: 0
szy Skew factor multiplier for skewing along the Z axis as you get farther from the Y axis. Default: 0
axy Angle to skew along the X axis as you get farther from the Y axis.
axz Angle to skew along the X axis as you get farther from the Z axis.
ayx Angle to skew along the Y axis as you get farther from the X axis.
ayz Angle to skew along the Y axis as you get farther from the Z axis.
azx Angle to skew along the Z axis as you get farther from the X axis.
azy Angle to skew along the Z axis as you get farther from the Y axis.

Example 1: Skew along the X axis in 2D.

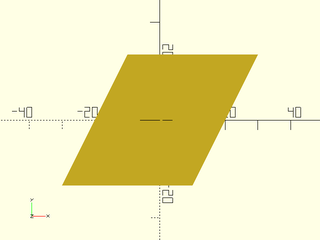
skew() Example 1 
include <BOSL2/std.scad>
skew(sxy=0.5) square(40, center=true);



Example 2: Skew along the X axis by 30º in 2D.

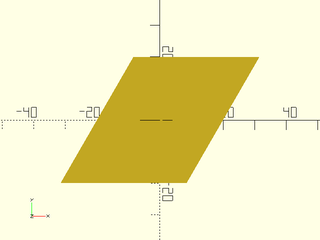
skew() Example 2 
include <BOSL2/std.scad>
skew(axy=30) square(40, center=true);



Example 3: Skew along the Y axis in 2D.

skew() Example 3 
include <BOSL2/std.scad>
skew(syx=0.5) square(40, center=true);



Example 4: Skew along the X axis in 3D as a factor of Y coordinate.

skew() Example 4 
include <BOSL2/std.scad>
skew(sxy=0.5) cube(40, center=true);



Example 5: Skew along the X axis in 3D as a factor of Z coordinate.

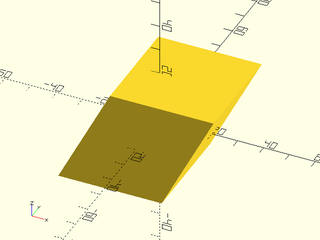
skew() Example 5 
include <BOSL2/std.scad>
skew(sxz=0.5) cube(40, center=true);



Example 6: Skew along the Y axis in 3D as a factor of X coordinate.

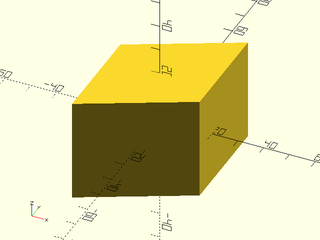
skew() Example 6 
include <BOSL2/std.scad>
skew(syx=0.5) cube(40, center=true);



Example 7: Skew along the Y axis in 3D as a factor of Z coordinate.

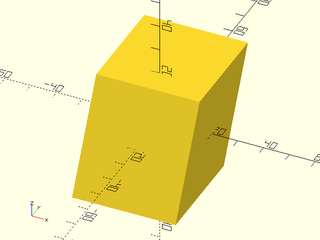
skew() Example 7 
include <BOSL2/std.scad>
skew(syz=0.5) cube(40, center=true);



Example 8: Skew along the Z axis in 3D as a factor of X coordinate.

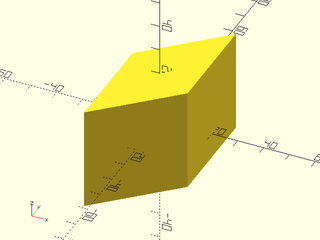
skew() Example 8 
include <BOSL2/std.scad>
skew(szx=0.5) cube(40, center=true);



Example 9: Skew along the Z axis in 3D as a factor of Y coordinate.

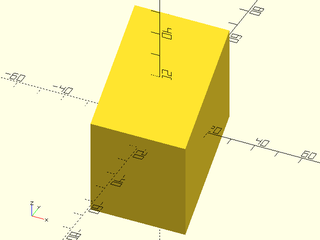
skew() Example 9 
include <BOSL2/std.scad>
skew(szy=0.75) cube(40, center=true);



Example 10: Skew Along Multiple Axes.

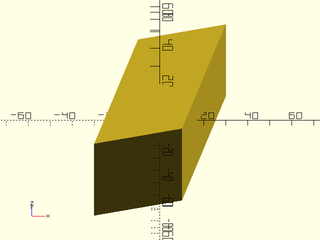
skew() Example 10 
include <BOSL2/std.scad>
skew(sxy=0.5, syx=0.3, szy=0.75) cube(40, center=true);



Example 11: Calling as a 2D Function

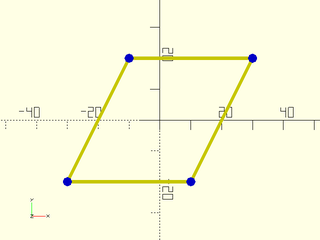
skew() Example 11 
include <BOSL2/std.scad>
pts = skew(p=square(40,center=true), sxy=0.5);
color("yellow") stroke(pts, closed=true);
color("blue") move_copies(pts) circle(d=3, $fn=8);



Example 12: Calling as a 3D Function

skew() Example 12 
include <BOSL2/std.scad>
pts = skew(p=path3d(square(40,center=true)), szx=0.5, szy=0.3);
stroke(pts,closed=true,dots=true,dots_color="blue");

Section: Applying transformation matrices to data

Function: apply()

Synopsis: Applies a transformation matrix to a point, list of points, array of points, or a VNF. [Path] [VNF] [Mat]

Topics: Affine, Matrices, Transforms

See Also: move(), rot(), scale(), skew()

Usage:

  • pts = apply(transform, points);

Description:

Applies the specified transformation matrix transform to a point, point list, bezier patch or VNF. When points contains 2D or 3D points the transform matrix may be a 4x4 affine matrix or a 3x4 matrix—the 4x4 matrix with its final row removed. When the data is 2D the matrix must not operate on the Z axis, except possibly by scaling it. When points contains 2D data you can also supply the transform as a 3x3 affine transformation matrix or the corresponding 2x3 matrix with the last row deleted.

Any other combination of matrices will produce an error, including acting with a 2D matrix (3x3) on 3D data. The output of apply is always the same dimension as the input—projections are not supported.

Note that a matrix with a negative determinant such as any mirror reflection flips the orientation of faces. If the transform matrix is square then apply() checks the determinant and if it is negative, apply() reverses the face order so that the transformed VNF has faces with the same winding direction as the original VNF. This adjustment applies only to VNFs, not to beziers or point lists.

Arguments:

By Position What it does
transform The 2D (3x3 or 2x3) or 3D (4x4 or 3x4) transformation matrix to apply.
points The point, point list, bezier patch, or VNF to apply the transformation to.

Example 1:

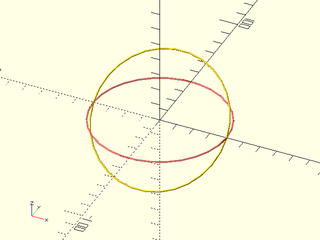
apply() Example 1 
include <BOSL2/std.scad>
path1 = path3d(circle(r=40));
tmat = xrot(45);
path2 = apply(tmat, path1);
#stroke(path1,closed=true);
stroke(path2,closed=true);



Example 2:

apply() Example 2 
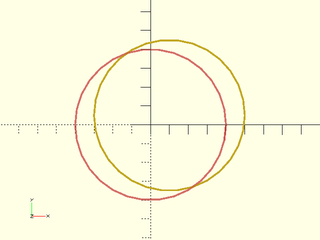
include <BOSL2/std.scad>
path1 = circle(r=40);
tmat = translate([10,5]);
path2 = apply(tmat, path1);
#stroke(path1,closed=true);
stroke(path2,closed=true);



Example 3:

apply() Example 3 
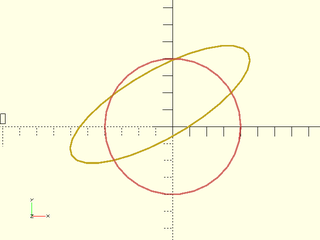
include <BOSL2/std.scad>
path1 = circle(r=40);
tmat = rot(30) * back(15) * scale([1.5,0.5,1]);
path2 = apply(tmat, path1);
#stroke(path1,closed=true);
stroke(path2,closed=true);



Home – Table of Contents – Functions Index – Topics – Cheat Sheet – Tutorials

Indices

Table of Contents
Function Index
Topics Index
Cheat Sheet
Tutorials

List of Files:

Basic Modeling:

Advanced Modeling:

Math:

Data Management:

Threaded Parts:

Parts:

Footnotes:

STD = Included in std.scad

Clone this wiki locally