-
Notifications
You must be signed in to change notification settings - Fork 115
beziers.scad
Bezier curves and surfaces are way to represent smooth curves and smoothly curving surfaces with a set of control points. The curve or surface is defined by the control points, but usually only passes through the first and last control point (the endpoints). This file provides some aids to constructing the control points, and highly optimized functions for computing the Bezier curves and surfaces given by the control points,
To use, add the following lines to the beginning of your file:
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
Terminology:
| Name | Definition |
|---|---|
| Path | A series of points joined by straight line segements. |
| Bezier Curve | A polynomial curve defined by a list of control points. The curve starts at the first control point and ends at the last one. The other control points define the shape of the curve and they are often NOT on the curve |
| Control Point | A point that influences the shape of the Bezier curve. |
| Degree | The degree of the polynomial used to make the bezier curve. A bezier curve of degree N will have N+1 control points. Most beziers are cubic (degree 3). The higher the degree, the more the curve can wiggle. |
| Bezier Parameter | A parameter, usually u below, that ranges from 0 to 1 to trace out the bezier curve. When u=0 you get the first control point and when u=1 you get the last control point. Intermediate points are traced out non-uniformly. |
| Bezier Path | A list of bezier control points corresponding to a series of Bezier curves that connect together, end to end. Because they connect, the endpoints are shared between control points and are not repeated, so a degree 3 bezier path representing two bezier curves will have seven entries to represent two sets of four control points. NOTE: A "bezier path" is NOT a standard path |
| Bezier Patch | A two-dimensional arrangement of Bezier control points that generate a bounded curved Bezier surface. A Bezier patch is a (N+1) by (M+1) grid of control points, which defines surface with four edges (in the non-degenerate case). |
| Bezier Surface | A surface defined by a list of one or more bezier patches. |
| Spline Steps | The number of straight-line segments used to approximate a Bezier curve. The more spline steps, the better the approximation to the curve, but the slower it will be to generate. This plays a role analogous to $fn for circles. Usually defaults to 16. |
-
-
bezier_points()– Computes one or more specified points along a bezier curve. [Path] -
bezier_curve()– Computes a specified number of points on a bezier curve. [Path] -
bezier_derivative()– Evaluates the derivative of the bezier curve at the given point or points. -
bezier_tangent()– Calculates unit tangent vectors along the bezier curve at one or more given positions. -
bezier_curvature()– Returns the curvature at one or more given positions along a bezier curve. -
bezier_closest_point()– Finds the closest position on a bezier curve to a given point. -
bezier_length()– Approximate the length of part of a bezier curve. -
bezier_line_intersection()– Calculates where a bezier curve intersects a line.
-
-
Section: Bezier Path Functions
-
bezpath_points()– Computes one or more specified points along a bezier path. [Path] -
bezpath_curve()– Converts bezier path into a path of points. [Path] -
bezpath_closest_point()– Finds the closest point on a bezier path to a given point. -
bezpath_length()– Approximate the length of a bezier path. -
path_to_bezpath()– Generates a bezier path that passes through all points in a given linear path. [Path] -
bezpath_close_to_axis()– Closes a 2D bezier path to the specified axis. [Path] -
bezpath_offset()– Forms a closed bezier path loop with a translated and reversed copy of itself. [Path]
-
-
Section: Cubic Bezier Path Construction
-
bez_begin()– Calculates starting bezier path control points. -
bez_tang()– Calculates control points for a smooth bezier path joint. -
bez_joint()– Calculates control points for a disjointed corner bezier path joint. -
bez_end()– Calculates ending bezier path control points.
-
-
-
is_bezier_patch()– Returns true if the given item is a bezier patch. -
bezier_patch_flat()– Creates a flat bezier patch. -
bezier_patch_reverse()– Reverses the orientation of a bezier patch. -
bezier_patch_points()– Computes one or more specified points across a bezier surface patch. -
bezier_vnf()– Generates a (probably non-manifold) VNF for one or more bezier surface patches. [VNF] -
bezier_vnf_degenerate_patch()– Generates a VNF for a degenerate bezier surface patch. [VNF] -
bezier_patch_normals()– Computes surface normals for one or more places on a bezier surface patch. -
bezier_sheet()– Creates a thin sheet from a bezier patch by extruding in normal to the patch [VNF]
-
-
-
debug_bezier()– Shows a bezier path and its associated control points. [Geom] -
debug_bezier_patches()– Shows a bezier surface patch and its associated control points. [Geom]
-
Synopsis: Computes one or more specified points along a bezier curve. [Path]
Topics: Bezier Curves
See Also: bezier_curve(), bezier_curvature(), bezier_tangent(), bezier_derivative()
Usage:
- pt = bezier_points(bezier, u);
- ptlist = bezier_points(bezier, RANGE);
- ptlist = bezier_points(bezier, LIST);
Description:
Computes points on a bezier curve with control points specified by bezier at parameter values
specified by u, which can be a scalar or a list. The value u=0 gives the first endpoint; u=1 gives the final endpoint,
and intermediate values of u fill in the curve in a non-uniform fashion. This function uses an optimized method which
is best when u is a long list and the bezier degree is 10 or less. The degree of the bezier
curve is len(bezier)-1.
Arguments:
| By Position | What it does |
|---|---|
bezier |
The list of endpoints and control points for this bezier curve. |
u |
Parameter values for evaluating the curve, given as a single value, a list or a range. |
Example 1: Quadratic (Degree 2) Bezier.
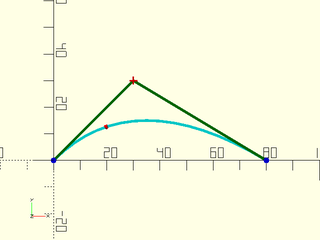
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bez = [[0,0], [30,30], [80,0]];
debug_bezier(bez, N=len(bez)-1);
translate(bezier_points(bez, 0.3)) color("red") sphere(1);
Example 2: Cubic (Degree 3) Bezier
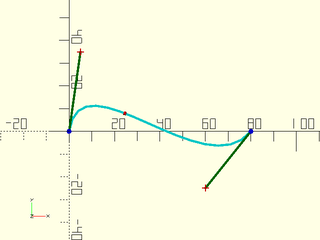
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bez = [[0,0], [5,35], [60,-25], [80,0]];
debug_bezier(bez, N=len(bez)-1);
translate(bezier_points(bez, 0.4)) color("red") sphere(1);
Example 3: Degree 4 Bezier.
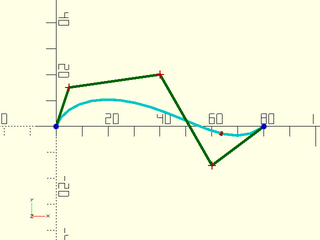
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bez = [[0,0], [5,15], [40,20], [60,-15], [80,0]];
debug_bezier(bez, N=len(bez)-1);
translate(bezier_points(bez, 0.8)) color("red") sphere(1);
Example 4: Giving a List of u
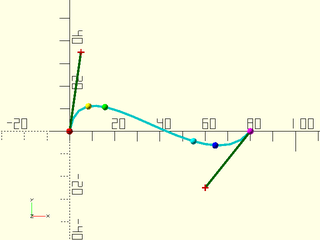
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bez = [[0,0], [5,35], [60,-25], [80,0]];
debug_bezier(bez, N=len(bez)-1);
pts = bezier_points(bez, [0, 0.2, 0.3, 0.7, 0.8, 1]);
rainbow(pts) move($item) sphere(1.5, $fn=12);
Example 5: Giving a Range of u
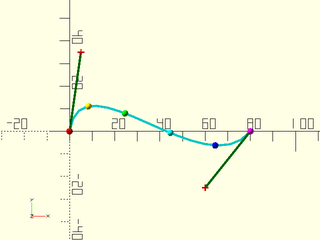
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bez = [[0,0], [5,35], [60,-25], [80,0]];
debug_bezier(bez, N=len(bez)-1);
pts = bezier_points(bez, [0:0.2:1]);
rainbow(pts) move($item) sphere(1.5, $fn=12);
Synopsis: Computes a specified number of points on a bezier curve. [Path]
Topics: Bezier Curves
See Also: bezier_curvature(), bezier_tangent(), bezier_derivative(), bezier_points()
Usage:
- path = bezier_curve(bezier, [splinesteps], [endpoint]);
Description:
Takes a list of bezier control points and generates splinesteps segments (splinesteps+1 points)
along the bezier curve they define.
Points start at the first control point and are sampled uniformly along the bezier parameter.
The endpoints of the output will be exactly equal to the first and last bezier control points
when endpoint is true. If endpoint is false the sampling stops one step before the final point
of the bezier curve, but you still get the same number of (more tightly spaced) points.
The distance between the points will not be equidistant.
The degree of the bezier curve is one less than the number of points in curve.
Arguments:
| By Position | What it does |
|---|---|
bezier |
The list of control points that define the Bezier curve. |
splinesteps |
The number of segments to create on the bezier curve. Default: 16 |
endpoint |
if false then exclude the endpoint. Default: True |
Example 1: Quadratic (Degree 2) Bezier.
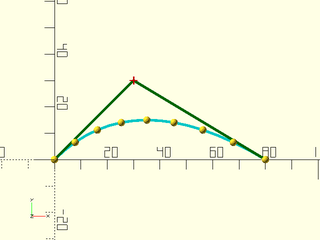
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bez = [[0,0], [30,30], [80,0]];
move_copies(bezier_curve(bez, 8)) sphere(r=1.5, $fn=12);
debug_bezier(bez, N=len(bez)-1);
Example 2: Cubic (Degree 3) Bezier
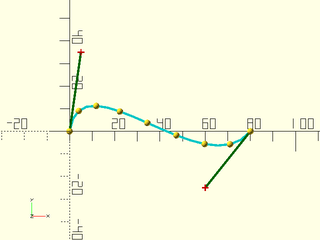
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bez = [[0,0], [5,35], [60,-25], [80,0]];
move_copies(bezier_curve(bez, 8)) sphere(r=1.5, $fn=12);
debug_bezier(bez, N=len(bez)-1);
Example 3: Degree 4 Bezier.
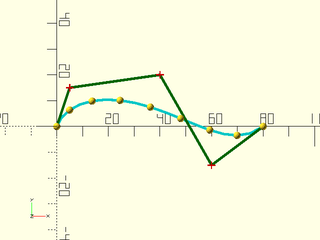
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bez = [[0,0], [5,15], [40,20], [60,-15], [80,0]];
move_copies(bezier_curve(bez, 8)) sphere(r=1.5, $fn=12);
debug_bezier(bez, N=len(bez)-1);
Synopsis: Evaluates the derivative of the bezier curve at the given point or points.
Topics: Bezier Curves
See Also: bezier_curvature(), bezier_tangent(), bezier_points()
Usage:
- deriv = bezier_derivative(bezier, u, [order]);
- derivs = bezier_derivative(bezier, LIST, [order]);
- derivs = bezier_derivative(bezier, RANGE, [order]);
Description:
Evaluates the derivative of the bezier curve at the given parameter value or values, u. The order gives the order of the derivative.
The degree of the bezier curve is one less than the number of points in bezier.
Arguments:
| By Position | What it does |
|---|---|
bezier |
The list of control points that define the Bezier curve. |
u |
Parameter values for evaluating the curve, given as a single value, a list or a range. |
order |
The order of the derivative to return. Default: 1 (for the first derivative) |
Synopsis: Calculates unit tangent vectors along the bezier curve at one or more given positions.
Topics: Bezier Curves
See Also: bezier_curvature(), bezier_derivative(), bezier_points()
Usage:
- tanvec = bezier_tangent(bezier, u);
- tanvecs = bezier_tangent(bezier, LIST);
- tanvecs = bezier_tangent(bezier, RANGE);
Description:
Returns the unit tangent vector at the given parameter values on a bezier curve with control points bezier.
Arguments:
| By Position | What it does |
|---|---|
bezier |
The list of control points that define the Bezier curve. |
u |
Parameter values for evaluating the curve, given as a single value, a list or a range. |
Synopsis: Returns the curvature at one or more given positions along a bezier curve.
Topics: Bezier Curves
See Also: bezier_tangent(), bezier_derivative(), bezier_points()
Usage:
- crv = bezier_curvature(curve, u);
- crvlist = bezier_curvature(curve, LIST);
- crvlist = bezier_curvature(curve, RANGE);
Description:
Returns the curvature value for the given parameters u on the bezier curve with control points bezier.
The curvature is the inverse of the radius of the tangent circle at the given point.
Thus, the tighter the curve, the larger the curvature value. Curvature will be 0 for
a position with no curvature, since 1/0 is not a number.
Arguments:
| By Position | What it does |
|---|---|
bezier |
The list of control points that define the Bezier curve. |
u |
Parameter values for evaluating the curve, given as a single value, a list or a range. |
Synopsis: Finds the closest position on a bezier curve to a given point.
Topics: Bezier Curves
See Also: bezier_points()
Usage:
- u = bezier_closest_point(bezier, pt, [max_err]);
Description:
Finds the closest part of the given bezier curve to point pt.
The degree of the curve, N, is one less than the number of points in curve.
Returns u for the closest position on the bezier curve to the given point pt.
Arguments:
| By Position | What it does |
|---|---|
bezier |
The list of control points that define the Bezier curve. |
pt |
The point to find the closest curve point to. |
max_err |
The maximum allowed error when approximating the closest approach. |
Example 1:

include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
pt = [40,15];
bez = [[0,0], [20,40], [60,-25], [80,0]];
u = bezier_closest_point(bez, pt);
debug_bezier(bez, N=len(bez)-1);
color("red") translate(pt) sphere(r=1);
color("blue") translate(bezier_points(bez,u)) sphere(r=1);
Synopsis: Approximate the length of part of a bezier curve.
Topics: Bezier Curves
See Also: bezier_points()
Usage:
- pathlen = bezier_length(bezier, [start_u], [end_u], [max_deflect]);
Description:
Approximates the length of the portion of the bezier curve between start_u and end_u.
Arguments:
| By Position | What it does |
|---|---|
bezier |
The list of control points that define the Bezier curve. |
start_u |
The Bezier parameter to start measuring measuring from. Between 0 and 1. |
end_u |
The Bezier parameter to end measuring at. Between 0 and 1. Greater than start_u. |
max_deflect |
The largest amount of deflection from the true curve to allow for approximation. |
Example 1:
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bez = [[0,0], [5,35], [60,-25], [80,0]];
echo(bezier_length(bez));
Synopsis: Calculates where a bezier curve intersects a line.
Topics: Bezier Curves, Geometry, Intersection
See Also: bezier_points(), bezier_length(), bezier_closest_point()
Usage:
- u = bezier_line_intersection(bezier, line);
Description:
Finds the intersection points of the 2D Bezier curve with control points bezier and the given line, specified as a pair of points.
Returns the intersection as a list of u values for the Bezier.
Arguments:
| By Position | What it does |
|---|---|
bezier |
The list of control points that define a 2D Bezier curve. |
line |
a list of two distinct 2d points defining a line |
To contruct more complicated curves you can connect a sequence of Bezier curves end to end.
A Bezier path is a flattened list of control points that, along with the degree, represents such a sequence of bezier curves where all of the curves have the same degree.
A Bezier path looks like a regular path, since it is just a list of points, but it is not a regular path. Use bezpath_curve() to convert a Bezier path to a regular path.
We interpret a degree N Bezier path as groups of N+1 control points that
share endpoints, so they overlap by one point. So if you have an order 3 bezier path [p0,p1,p2,p3,p4,p5,p6] then the first
Bezier curve control point set is [p0,p1,p2,p3] and the second one is [p3,p4,p5,p6]. The endpoint, p3, is shared between the control point sets.
The Bezier degree, which must be known to interpret the Bezier path, defaults to 3.
Synopsis: Computes one or more specified points along a bezier path. [Path]
Topics: Bezier Paths
See Also: bezier_points(), bezier_curve()
Usage:
- pt = bezpath_points(bezpath, curveind, u, [N]);
- ptlist = bezpath_points(bezpath, curveind, LIST, [N]);
- path = bezpath_points(bezpath, curveind, RANGE, [N]);
Description:
Extracts from the Bezier path bezpath the control points for the Bezier curve whose index is curveind and
computes the point or points on the corresponding Bezier curve specified by u. If curveind is zero you
get the first curve. The number of curves is (len(bezpath)-1)/N so the maximum index is that number minus one.
Arguments:
| By Position | What it does |
|---|---|
bezpath |
A Bezier path path to approximate. |
curveind |
Curve number along the path. |
u |
Parameter values for evaluating the curve, given as a single value, a list or a range. |
N |
The degree of the Bezier path curves. Default: 3 |
Synopsis: Converts bezier path into a path of points. [Path]
Topics: Bezier Paths
See Also: bezier_points(), bezier_curve(), bezpath_points()
Usage:
- path = bezpath_curve(bezpath, [splinesteps], [N], [endpoint])
Description:
Computes a number of uniformly distributed points along a bezier path.
Arguments:
| By Position | What it does |
|---|---|
bezpath |
A bezier path to approximate. |
splinesteps |
Number of straight lines to split each bezier curve into. default=16 |
N |
The degree of the bezier curves. Cubic beziers have N=3. Default: 3 |
endpoint |
If true, include the very last point of the bezier path. Default: true |
Example 1:
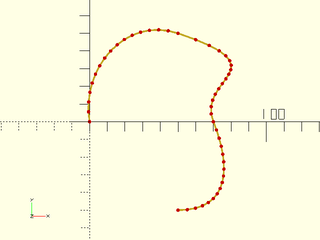
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bez = [
[0,0], [-5,30],
[20,60], [50,50], [110,30],
[60,25], [70,0], [80,-25],
[80,-50], [50,-50]
];
path = bezpath_curve(bez);
stroke(path,dots=true,dots_color="red");
Synopsis: Finds the closest point on a bezier path to a given point.
Topics: Bezier Paths
See Also: bezpath_points(), bezpath_curve(), bezier_points(), bezier_curve(), bezier_closest_point()
Usage:
- res = bezpath_closest_point(bezpath, pt, [N], [max_err]);
Description:
Finds an approximation to the closest part of the given bezier path to point pt.
Returns [segnum, u] for the closest position on the bezier path to the given point pt.
Arguments:
| By Position | What it does |
|---|---|
bezpath |
A bezier path to approximate. |
pt |
The point to find the closest curve point to. |
N |
The degree of the bezier curves. Cubic beziers have N=3. Default: 3 |
max_err |
The maximum allowed error when approximating the closest approach. |
Example 1:

include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
pt = [100,0];
bez = [[0,0], [20,40], [60,-25], [80,0],
[100,25], [140,25], [160,0]];
pos = bezpath_closest_point(bez, pt);
xy = bezpath_points(bez,pos[0],pos[1]);
debug_bezier(bez, N=3);
color("red") translate(pt) sphere(r=1);
color("blue") translate(xy) sphere(r=1);
Synopsis: Approximate the length of a bezier path.
Topics: Bezier Paths
See Also: bezier_points(), bezier_curve(), bezier_length()
Usage:
- plen = bezpath_length(path, [N], [max_deflect]);
Description:
Approximates the length of the bezier path.
Arguments:
| By Position | What it does |
|---|---|
path |
A bezier path to approximate. |
N |
The degree of the bezier curves. Cubic beziers have N=3. Default: 3 |
max_deflect |
The largest amount of deflection from the true curve to allow for approximation. |
Synopsis: Generates a bezier path that passes through all points in a given linear path. [Path]
Topics: Bezier Paths, Rounding
See Also: path_tangents()
Usage:
- bezpath = path_to_bezpath(path, [closed], [tangents], [uniform], [size=]|[relsize=]);
Description:
Given a 2d or 3d input path and optional list of tangent vectors, computes a cubic (degree 3) bezier
path that passes through every point on the input path and matches the tangent vectors. If you do
not supply the tangent it will be computed using path_tangents(). If the path is closed specify this
by setting closed=true. The size or relsize parameter determines how far the curve can deviate from
the input path. In the case where the curve has a single hump, the size specifies the exact distance
between the specified path and the bezier. If you give relsize then it is relative to the segment
length (e.g. 0.05 means 5% of the segment length). In 2d when the bezier curve makes an S-curve
the size parameter specifies the sum of the deviations of the two peaks of the curve. In 3-space
the bezier curve may have three extrema: two maxima and one minimum. In this case the size specifies
the sum of the maxima minus the minimum. If you do not supply the tangents then they are computed
using path_tangents() with uniform=false by default. Tangents computed on non-uniform data tend
to display overshoots. See smooth_path() for examples.
Arguments:
| By Position | What it does |
|---|---|
path |
2D or 3D point list or 1-region that the curve must pass through |
closed |
true if the curve is closed . Default: false |
tangents |
tangents constraining curve direction at each point |
uniform |
set to true to compute tangents with uniform=true. Default: false |
| By Name | What it does |
|---|---|
size |
absolute size specification for the curve, a number or vector |
relsize |
relative size specification for the curve, a number or vector. Default: 0.1. |
Synopsis: Closes a 2D bezier path to the specified axis. [Path]
Topics: Bezier Paths
See Also: bezpath_offset()
Usage:
- bezpath = bezpath_close_to_axis(bezpath, [axis], [N]);
Description:
Takes a 2D bezier path and closes it to the specified axis.
Arguments:
| By Position | What it does |
|---|---|
bezpath |
The 2D bezier path to close to the axis. |
axis |
The axis to close to, "X", or "Y". Default: "X" |
N |
The degree of the bezier curves. Cubic beziers have N=3. Default: 3 |
Example 1:
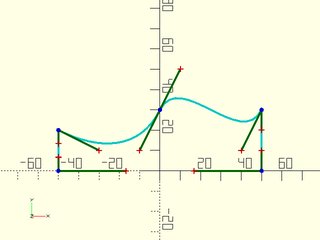
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bez = [[50,30], [40,10], [10,50], [0,30],
[-10, 10], [-30,10], [-50,20]];
closed = bezpath_close_to_axis(bez);
debug_bezier(closed);
Example 2:
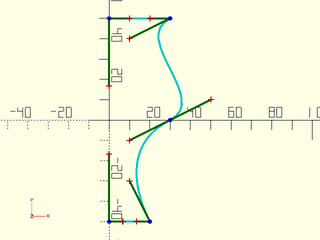
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bez = [[30,50], [10,40], [50,10], [30,0],
[10, -10], [10,-30], [20,-50]];
closed = bezpath_close_to_axis(bez, axis="Y");
debug_bezier(closed);
Synopsis: Forms a closed bezier path loop with a translated and reversed copy of itself. [Path]
Topics: Bezier Paths
See Also: bezpath_close_to_axis()
Usage:
- bezpath = bezpath_offset(offset, bezier, [N]);
Description:
Takes a 2D bezier path and closes it with a matching reversed path that is offset by the given offset [X,Y] distance.
Arguments:
| By Position | What it does |
|---|---|
offset |
Amount to offset second path by. |
bezier |
The 2D bezier path. |
N |
The degree of the bezier curves. Cubic beziers have N=3. Default: 3 |
Example 1:
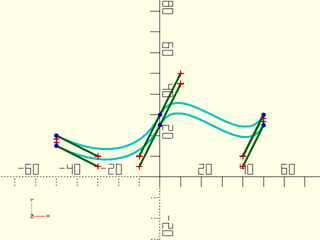
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bez = [[50,30], [40,10], [10,50], [0,30], [-10, 10], [-30,10], [-50,20]];
closed = bezpath_offset([0,-5], bez);
debug_bezier(closed);
Example 2:

include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bez = [[30,50], [10,40], [50,10], [30,0], [10, -10], [10,-30], [20,-50]];
closed = bezpath_offset([-5,0], bez);
debug_bezier(closed);
Synopsis: Calculates starting bezier path control points.
Topics: Bezier Paths
See Also: bez_tang(), bez_joint(), bez_end()
Usage:
- pts = bez_begin(pt, a, r, [p=]);
- pts = bez_begin(pt, VECTOR, [r], [p=]);
Description:
This is used to create the first endpoint and control point of a cubic bezier path.
Arguments:
| By Position | What it does |
|---|---|
pt |
The starting endpoint for the bezier path. |
a |
If given a scalar, specifies the theta (XY plane) angle in degrees from X+. If given a vector, specifies the direction and possibly distance of the first control point. |
r |
Specifies the distance of the control point from the endpoint pt. |
| By Name | What it does |
|---|---|
p |
If given, specifies the number of degrees away from the Z+ axis. |
Example 1: 2D Bezier Path by Angle
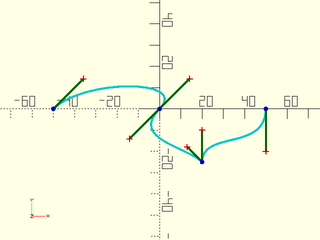
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bezpath = flatten([
bez_begin([-50, 0], 45,20),
bez_tang ([ 0, 0],-135,20),
bez_joint([ 20,-25], 135, 90, 10, 15),
bez_end ([ 50, 0], -90,20),
]);
debug_bezier(bezpath);
Example 2: 2D Bezier Path by Vector
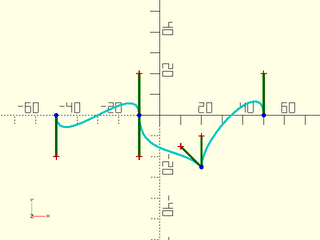
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bezpath = flatten([
bez_begin([-50,0],[0,-20]),
bez_tang ([-10,0],[0,-20]),
bez_joint([ 20,-25], [-10,10], [0,15]),
bez_end ([ 50,0],[0, 20]),
]);
debug_bezier(bezpath);
Example 3: 2D Bezier Path by Vector and Distance
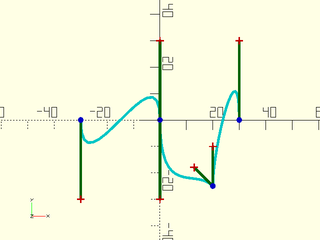
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bezpath = flatten([
bez_begin([-30,0],FWD, 30),
bez_tang ([ 0,0],FWD, 30),
bez_joint([ 20,-25], 135, 90, 10, 15),
bez_end ([ 30,0],BACK,30),
]);
debug_bezier(bezpath);
Example 4: 3D Bezier Path by Angle
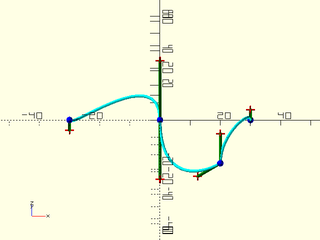
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bezpath = flatten([
bez_begin([-30,0,0],90,20,p=135),
bez_tang ([ 0,0,0],-90,20,p=135),
bez_joint([20,-25,0], 135, 90, 15, 10, p1=135, p2=45),
bez_end ([ 30,0,0],-90,20,p=45),
]);
debug_bezier(bezpath);
Example 5: 3D Bezier Path by Vector
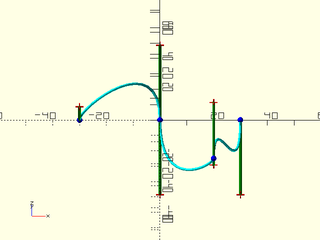
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bezpath = flatten([
bez_begin([-30,0,0],[0,-20, 20]),
bez_tang ([ 0,0,0],[0,-20,-20]),
bez_joint([20,-25,0],[0,10,-10],[0,15,15]),
bez_end ([ 30,0,0],[0,-20,-20]),
]);
debug_bezier(bezpath);
Example 6: 3D Bezier Path by Vector and Distance
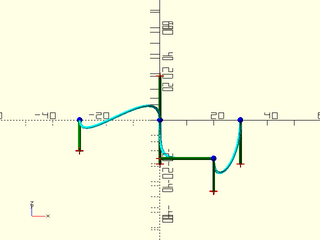
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bezpath = flatten([
bez_begin([-30,0,0],FWD, 20),
bez_tang ([ 0,0,0],DOWN,20),
bez_joint([20,-25,0],LEFT,DOWN,r1=20,r2=15),
bez_end ([ 30,0,0],DOWN,20),
]);
debug_bezier(bezpath);
Synopsis: Calculates control points for a smooth bezier path joint.
Topics: Bezier Paths
See Also: bez_begin(), bez_joint(), bez_end()
Usage:
- pts = bez_tang(pt, a, r1, r2, [p=]);
- pts = bez_tang(pt, VECTOR, [r1], [r2], [p=]);
Description:
This creates a smooth joint in a cubic bezier path. It creates three points, being the
approaching control point, the fixed bezier control point, and the departing control
point. The two control points will be collinear with the fixed point, making for a
smooth bezier curve at the fixed point. See bez_begin() for examples.
Arguments:
| By Position | What it does |
|---|---|
pt |
The fixed point for the bezier path. |
a |
If given a scalar, specifies the theta (XY plane) angle in degrees from X+. If given a vector, specifies the direction and possibly distance of the departing control point. |
r1 |
Specifies the distance of the approching control point from the fixed point. Overrides the distance component of the vector if a contains a vector. |
r2 |
Specifies the distance of the departing control point from the fixed point. Overrides the distance component of the vector if a contains a vector. If r1 is given and r2 is not, uses the value of r1 for r2. |
| By Name | What it does |
|---|---|
p |
If given, specifies the number of degrees away from the Z+ axis. |
Synopsis: Calculates control points for a disjointed corner bezier path joint.
Topics: Bezier Paths
See Also: bez_begin(), bez_tang(), bez_end()
Usage:
- pts = bez_joint(pt, a1, a2, r1, r2, [p1=], [p2=]);
- pts = bez_joint(pt, VEC1, VEC2, [r1=], [r2=], [p1=], [p2=]);
Description:
This creates a disjoint corner joint in a cubic bezier path. It creates three points, being
the aproaching control point, the fixed bezier control point, and the departing control point.
The two control points can be directed in different arbitrary directions from the fixed bezier
point. See bez_begin() for examples.
Arguments:
| By Position | What it does |
|---|---|
pt |
The fixed point for the bezier path. |
a1 |
If given a scalar, specifies the theta (XY plane) angle in degrees from X+. If given a vector, specifies the direction and possibly distance of the approaching control point. |
a2 |
If given a scalar, specifies the theta (XY plane) angle in degrees from X+. If given a vector, specifies the direction and possibly distance of the departing control point. |
r1 |
Specifies the distance of the approching control point from the fixed point. Overrides the distance component of the vector if a1 contains a vector. |
r2 |
Specifies the distance of the departing control point from the fixed point. Overrides the distance component of the vector if a2 contains a vector. |
| By Name | What it does |
|---|---|
p1 |
If given, specifies the number of degrees away from the Z+ axis of the approaching control point. |
p2 |
If given, specifies the number of degrees away from the Z+ axis of the departing control point. |
Synopsis: Calculates ending bezier path control points.
Topics: Bezier Paths
See Also: bez_tang(), bez_joint()
Usage:
- pts = bez_end(pt, a, r, [p=]);
- pts = bez_end(pt, VECTOR, [r], [p=]);
Description:
This is used to create the approaching control point, and the endpoint of a cubic bezier path.
See bez_begin() for examples.
Arguments:
| By Position | What it does |
|---|---|
pt |
The starting endpoint for the bezier path. |
a |
If given a scalar, specifies the theta (XY plane) angle in degrees from X+. If given a vector, specifies the direction and possibly distance of the first control point. |
r |
Specifies the distance of the control point from the endpoint pt. |
p |
If given, specifies the number of degrees away from the Z+ axis. |
Synopsis: Returns true if the given item is a bezier patch.
Topics: Bezier Patches, Type Checking
Usage:
- bool = is_bezier_patch(x);
Description:
Returns true if the given item is a bezier patch. (a 2D array of 3D points.)
Arguments:
| By Position | What it does |
|---|---|
x |
The value to check the type of. |
Synopsis: Creates a flat bezier patch.
Topics: Bezier Patches
See Also: bezier_patch_points()
Usage:
- patch = bezier_patch_flat(size, [N=], [spin=], [orient=], [trans=]);
Description:
Returns a flat rectangular bezier patch of degree N, centered on the XY plane.
Arguments:
| By Position | What it does |
|---|---|
size |
scalar or 2-vector giving the X and Y dimensions of the patch. |
| By Name | What it does |
|---|---|
N |
Degree of the patch to generate. Since this is flat, a degree of 1 should usually be sufficient. Default: 1 |
orient |
A direction vector. Point the patch normal in this direction. |
spin |
Spin angle to apply to the patch |
trans |
Amount to translate patch, after orient and spin. |
Example 1:
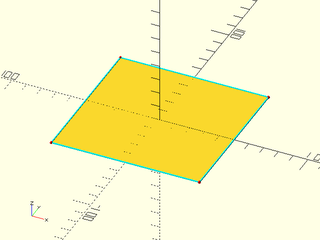
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
patch = bezier_patch_flat(size=[100,100]);
debug_bezier_patches([patch], size=1, showcps=true);
Synopsis: Reverses the orientation of a bezier patch.
Topics: Bezier Patches
See Also: bezier_patch_points(), bezier_patch_flat()
Usage:
- rpatch = bezier_patch_reverse(patch);
Description:
Reverses the patch, so that the faces generated from it are flipped back to front.
Arguments:
| By Position | What it does |
|---|---|
patch |
The patch to reverse. |
Synopsis: Computes one or more specified points across a bezier surface patch.
Topics: Bezier Patches
See Also: bezier_patch_normals(), bezier_points(), bezier_curve(), bezpath_curve()
Usage:
- pt = bezier_patch_points(patch, u, v);
- ptgrid = bezier_patch_points(patch, LIST, LIST);
- ptgrid = bezier_patch_points(patch, RANGE, RANGE);
Description:
Sample a bezier patch on a listed point set. The bezier patch must be a rectangular array of points, and it will be sampled at all the (u,v) pairs that you specify. If you give u and v as single numbers you'll get a single point back. If you give u and v as lists or ranges you'll get a 2d rectangular array of points. If one but not both of u and v is a list or range then you'll get a list of points.
Arguments:
| By Position | What it does |
|---|---|
patch |
The 2D array of control points for a Bezier patch. |
u |
The bezier u parameter (inner list of patch). Generally between 0 and 1. Can be a list, range or value. |
v |
The bezier v parameter (outer list of patch). Generally between 0 and 1. Can be a list, range or value. |
Example 1:

include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
patch = [
[[-50,-50, 0], [-16,-50, 20], [ 16,-50, 20], [50,-50, 0]],
[[-50,-16, 20], [-16,-16, 40], [ 16,-16, 40], [50,-16, 20]],
[[-50, 16, 20], [-16, 16, 40], [ 16, 16, 40], [50, 16, 20]],
[[-50, 50, 0], [-16, 50, 20], [ 16, 50, 20], [50, 50, 0]]
];
debug_bezier_patches(patches=[patch], size=1, showcps=true);
pt = bezier_patch_points(patch, 0.6, 0.75);
translate(pt) color("magenta") sphere(d=3, $fn=12);
Example 2: Getting Multiple Points at Once

include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
patch = [
[[-50,-50, 0], [-16,-50, 20], [ 16,-50, 20], [50,-50, 0]],
[[-50,-16, 20], [-16,-16, 40], [ 16,-16, 40], [50,-16, 20]],
[[-50, 16, 20], [-16, 16, 40], [ 16, 16, 40], [50, 16, 20]],
[[-50, 50, 0], [-16, 50, 20], [ 16, 50, 20], [50, 50, 0]]
];
debug_bezier_patches(patches=[patch], size=1, showcps=true);
pts = bezier_patch_points(patch, [0:0.2:1], [0:0.2:1]);
for (row=pts) move_copies(row) color("magenta") sphere(d=3, $fn=12);
Synopsis: Generates a (probably non-manifold) VNF for one or more bezier surface patches. [VNF]
Topics: Bezier Patches
See Also: bezier_patch_points(), bezier_patch_flat()
Usage:
- vnf = bezier_vnf(patches, [splinesteps], [style]);
Description:
Convert a patch or list of patches into the corresponding Bezier surface, representing the
result as a VNF structure. The splinesteps argument specifies the sampling grid of
the surface for each patch by specifying the number of segments on the borders of the surface.
It can be a scalar, which gives a uniform grid, or
it can be [USTEPS, VSTEPS], which gives difference spacing in the U and V parameters.
Note that the surface you produce may be disconnected and is not necessarily a valid manifold in OpenSCAD.
You must also ensure that the patches mate exactly along their edges, or the VNF will be invalid.
Arguments:
| By Position | What it does |
|---|---|
patches |
The bezier patch or list of bezier patches to convert into a vnf. |
splinesteps |
Number of segments on the border of the bezier surface. You can specify [USTEPS,VSTEPS]. Default: 16 |
style |
The style of subdividing the quads into faces. Valid options are "default", "alt", "min_edge", "quincunx", "convex" and "concave". See vnf_vertex_array(). Default: "default" |
Example 1:
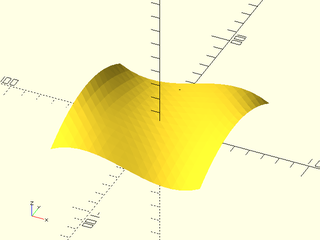
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
patch = [
// u=0,v=0 u=1,v=0
[[-50,-50, 0], [-16,-50, 20], [ 16,-50, -20], [50,-50, 0]],
[[-50,-16, 20], [-16,-16, 20], [ 16,-16, -20], [50,-16, 20]],
[[-50, 16, 20], [-16, 16, -20], [ 16, 16, 20], [50, 16, 20]],
[[-50, 50, 0], [-16, 50, -20], [ 16, 50, 20], [50, 50, 0]],
// u=0,v=1 u=1,v=1
];
vnf = bezier_vnf(patch, splinesteps=16);
vnf_polyhedron(vnf);
Example 2: Combining multiple patches
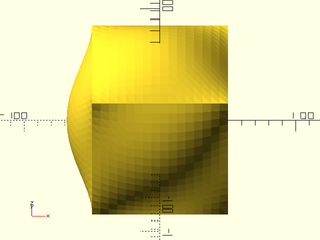
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
patch = 100*[
// u=0,v=0 u=1,v=0
[[0, 0,0], [1/3, 0, 0], [2/3, 0, 0], [1, 0,0]],
[[0,1/3,0], [1/3,1/3,1/3], [2/3,1/3,1/3], [1,1/3,0]],
[[0,2/3,0], [1/3,2/3,1/3], [2/3,2/3,1/3], [1,2/3,0]],
[[0, 1,0], [1/3, 1, 0], [2/3, 1, 0], [1, 1,0]],
// u=0,v=1 u=1,v=1
];
fpatch = bezier_patch_flat([100,100]);
tpatch = translate([-50,-50,50], patch);
flatpatch = translate([0,0,50], fpatch);
vnf = bezier_vnf([
tpatch,
xrot(90, tpatch),
xrot(-90, tpatch),
xrot(180, tpatch),
yrot(90, flatpatch),
yrot(-90, tpatch)]);
vnf_polyhedron(vnf);
Example 3:
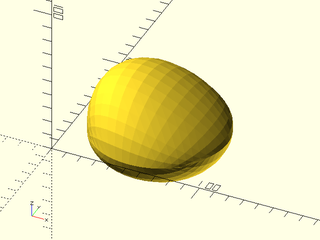
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
patch1 = [
[[18,18,0], [33, 0, 0], [ 67, 0, 0], [ 82, 18,0]],
[[ 0,40,0], [ 0, 0,100], [100, 0, 20], [100, 40,0]],
[[ 0,60,0], [ 0,100,100], [100,100, 20], [100, 60,0]],
[[18,82,0], [33,100, 0], [ 67,100, 0], [ 82, 82,0]],
];
patch2 = [
[[18,82,0], [33,100, 0], [ 67,100, 0], [ 82, 82,0]],
[[ 0,60,0], [ 0,100,-50], [100,100,-50], [100, 60,0]],
[[ 0,40,0], [ 0, 0,-50], [100, 0,-50], [100, 40,0]],
[[18,18,0], [33, 0, 0], [ 67, 0, 0], [ 82, 18,0]],
];
vnf = bezier_vnf(patches=[patch1, patch2], splinesteps=16);
vnf_polyhedron(vnf);
Example 4: Connecting Patches with asymmetric splinesteps. Note it is fastest to join all the VNFs at once, which happens in vnf_polyhedron, rather than generating intermediate joined partial surfaces.

include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
steps = 8;
edge_patch = [
// u=0, v=0 u=1,v=0
[[-60, 0,-40], [0, 0,-40], [60, 0,-40]],
[[-60, 0, 0], [0, 0, 0], [60, 0, 0]],
[[-60,40, 0], [0,40, 0], [60,40, 0]],
// u=0, v=1 u=1,v=1
];
corner_patch = [
// u=0, v=0 u=1,v=0
[[ 0, 40,-40], [ 0, 0,-40], [40, 0,-40]],
[[ 0, 40, 0], [ 0, 0, 0], [40, 0, 0]],
[[40, 40, 0], [40, 40, 0], [40, 40, 0]],
// u=0, v=1 u=1,v=1
];
face_patch = bezier_patch_flat([120,120],orient=LEFT);
edges = [
for (axrot=[[0,0,0],[0,90,0],[0,0,90]], xang=[-90:90:180])
bezier_vnf(
splinesteps=[steps,1],
rot(a=axrot,
p=rot(a=[xang,0,0],
p=translate(v=[0,-100,100],p=edge_patch)
)
)
)
];
corners = [
for (xang=[0,180], zang=[-90:90:180])
bezier_vnf(
splinesteps=steps,
rot(a=[xang,0,zang],
p=translate(v=[-100,-100,100],p=corner_patch)
)
)
];
faces = [
for (axrot=[[0,0,0],[0,90,0],[0,0,90]], zang=[0,180])
bezier_vnf(
splinesteps=1,
rot(a=axrot,
p=zrot(zang,move([-100,0,0], face_patch))
)
)
];
vnf_polyhedron(concat(edges,corners,faces));
Synopsis: Generates a VNF for a degenerate bezier surface patch. [VNF]
Topics: Bezier Patches
See Also: bezier_patch_points(), bezier_patch_flat(), bezier_vnf()
Usage:
- vnf = bezier_vnf_degenerate_patch(patch, [splinesteps], [reverse]);
- vnf_edges = bezier_vnf_degenerate_patch(patch, [splinesteps], [reverse], return_edges=true);
Description:
Returns a VNF for a degenerate rectangular bezier patch where some of the corners of the patch are equal. If the resulting patch has no faces then returns an empty VNF. Note that due to the degeneracy, the shape of the surface can be triangular even though the underlying patch is a rectangle. If you specify return_edges then the return is a list whose first element is the vnf and whose second element lists the edges in the order [left, right, top, bottom], where each list is a list of the actual point values, but possibly only a single point if that edge is degenerate. The method checks for various types of degeneracy and uses a triangular or partly triangular array of sample points. See examples below for the types of degeneracy detected and how the patch is sampled for those cases. Note that splinesteps is the same for both directions of the patch, so it cannot be an array.
Arguments:
| By Position | What it does |
|---|---|
patch |
Patch to process |
splinesteps |
Number of segments to produce on each side. Default: 16 |
reverse |
reverse direction of faces. Default: false |
return_edges |
if true return the points on the four edges: [left, right, top, bottom]. Default: false |
Example 1: This quartic patch is degenerate at one corner, where a row of control points are equal. Processing this degenerate patch normally produces excess triangles near the degenerate point.
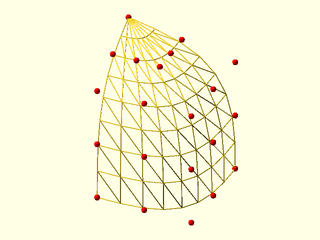
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
splinesteps=8;
patch=[
repeat([-12.5, 12.5, 15],5),
[[-6.25, 11.25, 15], [-6.25, 8.75, 15], [-6.25, 6.25, 15], [-8.75, 6.25, 15], [-11.25, 6.25, 15]],
[[0, 10, 15], [0, 5, 15], [0, 0, 15], [-5, 0, 15], [-10, 0, 15]],
[[0, 10, 8.75], [0, 5, 8.75], [0, 0, 8.75], [-5, 0, 8.75], [-10, 0, 8.75]],
[[0, 10, 2.5], [0, 5, 2.5], [0, 0, 2.5], [-5, 0, 2.5], [-10, 0, 2.5]]
];
vnf_wireframe((bezier_vnf(patch, splinesteps)),width=0.1);
color("red")move_copies(flatten(patch)) sphere(r=0.3,$fn=9);
Example 2: With bezier_vnf_degenerate_patch the degenerate point does not have excess triangles. The top half of the patch decreases the number of sampled points by 2 for each row.
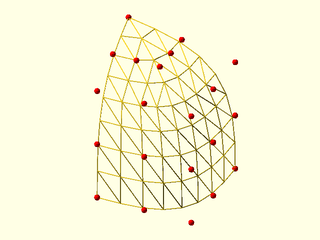
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
splinesteps=8;
patch=[
repeat([-12.5, 12.5, 15],5),
[[-6.25, 11.25, 15], [-6.25, 8.75, 15], [-6.25, 6.25, 15], [-8.75, 6.25, 15], [-11.25, 6.25, 15]],
[[0, 10, 15], [0, 5, 15], [0, 0, 15], [-5, 0, 15], [-10, 0, 15]],
[[0, 10, 8.75], [0, 5, 8.75], [0, 0, 8.75], [-5, 0, 8.75], [-10, 0, 8.75]],
[[0, 10, 2.5], [0, 5, 2.5], [0, 0, 2.5], [-5, 0, 2.5], [-10, 0, 2.5]]
];
vnf_wireframe(bezier_vnf_degenerate_patch(patch, splinesteps),width=0.1);
color("red")move_copies(flatten(patch)) sphere(r=0.3,$fn=9);
Example 3: With splinesteps odd you get one "odd" row where the point count decreases by 1 instead of 2. You may prefer even values for splinesteps to avoid this.
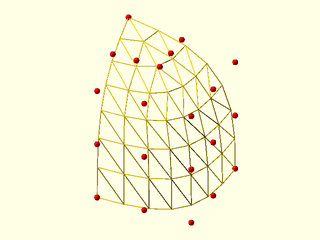
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
splinesteps=7;
patch=[
repeat([-12.5, 12.5, 15],5),
[[-6.25, 11.25, 15], [-6.25, 8.75, 15], [-6.25, 6.25, 15], [-8.75, 6.25, 15], [-11.25, 6.25, 15]],
[[0, 10, 15], [0, 5, 15], [0, 0, 15], [-5, 0, 15], [-10, 0, 15]],
[[0, 10, 8.75], [0, 5, 8.75], [0, 0, 8.75], [-5, 0, 8.75], [-10, 0, 8.75]],
[[0, 10, 2.5], [0, 5, 2.5], [0, 0, 2.5], [-5, 0, 2.5], [-10, 0, 2.5]]
];
vnf_wireframe(bezier_vnf_degenerate_patch(patch, splinesteps),width=0.1);
color("red")move_copies(flatten(patch)) sphere(r=0.3,$fn=9);
Example 4: A more extreme degeneracy occurs when the top half of a patch is degenerate to a line. (For odd length patches the middle row must be degenerate to trigger this style.) In this case the number of points in each row decreases by 1 for every row. It doesn't matter if splinesteps is odd or even.
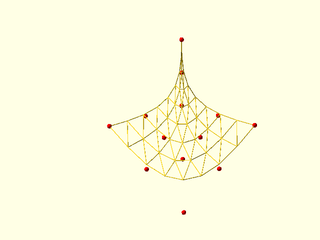
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
splinesteps=8;
patch = [[[10, 0, 0], [10, -10.4, 0], [10, -20.8, 0], [1.876, -14.30, 0], [-6.24, -7.8, 0]],
[[5, 0, 0], [5, -5.2, 0], [5, -10.4, 0], [0.938, -7.15, 0], [-3.12, -3.9, 0]],
repeat([0,0,0],5),
repeat([0,0,5],5),
repeat([0,0,10],5)
];
vnf_wireframe(bezier_vnf_degenerate_patch(patch, splinesteps),width=0.1);
color("red")move_copies(flatten(patch)) sphere(r=0.3,$fn=9);
Example 5: Here is a degenerate cubic patch.
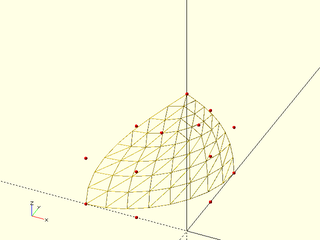
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
splinesteps=8;
patch = [ [ [-20,0,0], [-10,0,0],[0,10,0],[0,20,0] ],
[ [-20,0,10], [-10,0,10],[0,10,10],[0,20,10]],
[ [-10,0,20], [-5,0,20], [0,5,20], [0,10,20]],
repeat([0,0,30],4)
];
color("red")move_copies(flatten(patch)) sphere(r=0.3,$fn=9);
vnf_wireframe(bezier_vnf_degenerate_patch(patch, splinesteps),width=0.1);
Example 6: A more extreme degenerate cubic patch, where two rows are equal.
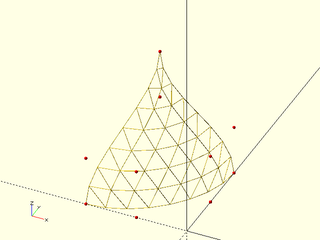
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
splinesteps=8;
patch = [ [ [-20,0,0], [-10,0,0],[0,10,0],[0,20,0] ],
[ [-20,0,10], [-10,0,10],[0,10,10],[0,20,10] ],
repeat([-10,10,20],4),
repeat([-10,10,30],4)
];
color("red")move_copies(flatten(patch)) sphere(r=0.3,$fn=9);
vnf_wireframe(bezier_vnf_degenerate_patch(patch, splinesteps),width=0.1);
Example 7: Quadratic patch degenerate at the right side:
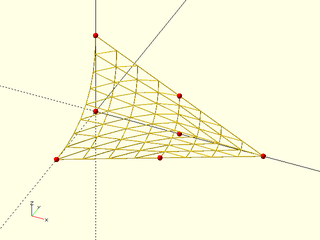
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
splinesteps=8;
patch = [[[0, -10, 0],[10, -5, 0],[20, 0, 0]],
[[0, 0, 0], [10, 0, 0], [20, 0, 0]],
[[0, 0, 10], [10, 0, 5], [20, 0, 0]]];
vnf_wireframe(bezier_vnf_degenerate_patch(patch, splinesteps),width=0.1);
color("red")move_copies(flatten(patch)) sphere(r=0.3,$fn=9);
Example 8: Cubic patch degenerate at both ends. In this case the point count changes by 2 at every row.
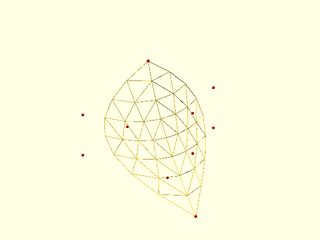
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
splinesteps=8;
patch = [
repeat([10,-10,0],4),
[ [-20,0,0], [-1,0,0],[0,10,0],[0,20,0] ],
[ [-20,0,10], [-10,0,10],[0,10,10],[0,20,10] ],
repeat([-10,10,20],4),
];
vnf_wireframe(bezier_vnf_degenerate_patch(patch, splinesteps),width=0.1);
color("red")move_copies(flatten(patch)) sphere(r=0.3,$fn=9);
Synopsis: Computes surface normals for one or more places on a bezier surface patch.
Topics: Bezier Patches
See Also: bezier_patch_points(), bezier_points(), bezier_curve(), bezpath_curve()
Usage:
- n = bezier_patch_normals(patch, u, v);
- ngrid = bezier_patch_normals(patch, LIST, LIST);
- ngrid = bezier_patch_normals(patch, RANGE, RANGE);
Description:
Compute the unit normal vector to a bezier patch at the listed point set. The bezier patch must be a rectangular array of points, and the normal will be computed at all the (u,v) pairs that you specify. If you give u and v as single numbers you'll get a single point back. If you give u and v as lists or ranges you'll get a 2d rectangular array of points. If one but not both of u and v is a list or range then you'll get a list of points.
This function works by computing the cross product of the tangents. In some degenerate cases the one of the tangents can be zero, so the normal vector does not exist. In this case, undef is returned. Another degenerate case occurs when the tangents are parallel, or nearly parallel. In this case you will get a unit vector returned but it will not be the correct normal vector. This can happen if you use a degenerate patch, or if you give two of the edges of your patch a smooth "corner" so that the u and v directions are parallel at the corner.
Arguments:
| By Position | What it does |
|---|---|
patch |
The 2D array of control points for a Bezier patch. |
u |
The bezier u parameter (inner list of patch). Generally between 0 and 1. Can be a list, range or value. |
v |
The bezier v parameter (outer list of patch). Generally between 0 and 1. Can be a list, range or value. |
Example 1: Normal vectors on a patch

include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
patch = [
// u=0,v=0 u=1,v=0
[[-50,-50, 0], [-16,-50, 20], [ 16,-50, -20], [50,-50, 0]],
[[-50,-16, 40], [-16,-16, 20], [ 16,-16, -20], [50,-16, 70]],
[[-50, 16, 20], [-16, 16, -20], [ 16, 37, 20], [70, 16, 20]],
[[-50, 50, 0], [73, 50, -40], [ 16, 50, 20], [50, 50, 0]],
// u=0,v=1 u=1,v=1
];
vnf_polyhedron(bezier_vnf(patch,splinesteps=30));
uv = lerpn(0,1,12);
pts = bezier_patch_points(patch, uv, uv);
normals = bezier_patch_normals(patch, uv, uv);
for(i=idx(uv),j=idx(uv)){
stroke([pts[i][j],pts[i][j]-6*normals[i][j]], width=0.5,
endcap1="dot",endcap2="arrow2",color="blue");
}
Example 2: This example gives invalid normal vectors at the four corners of the patch where the u and v directions are parallel. You can see how the line of triangulation is approaching parallel at the edge, and the invalid vectors in red point in a completely incorrect direction.
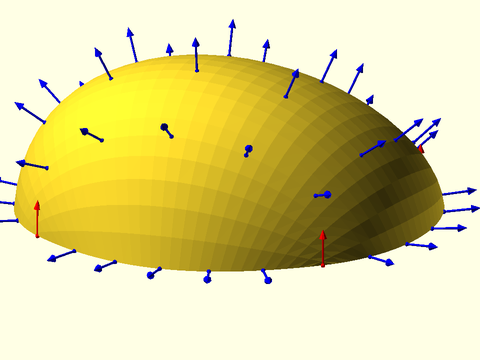
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
patch = [
[[18,18,0], [33, 0, 0], [ 67, 0, 0], [ 82, 18,0]],
[[ 0,40,0], [ 0, 0,100], [100, 0, 20], [100, 40,0]],
[[ 0,60,0], [ 0,100,100], [100,100, 20], [100, 60,0]],
[[18,82,0], [33,100, 0], [ 67,100, 0], [ 82, 82,0]],
];
vnf_polyhedron(bezier_vnf(patch,splinesteps=30));
uv = lerpn(0,1,7);
pts = bezier_patch_points(patch, uv, uv);
normals = bezier_patch_normals(patch, uv, uv);
for(i=idx(uv),j=idx(uv)){
color=((uv[i]==0 || uv[i]==1) && (uv[j]==0 || uv[j]==1))
? "red" : "blue";
stroke([pts[i][j],pts[i][j]-8*normals[i][j]], width=0.5,
endcap1="dot",endcap2="arrow2",color=color);
}
Example 3: This degenerate patch has normals everywhere, but computation of the normal fails at the point of degeneracy, the top corner.
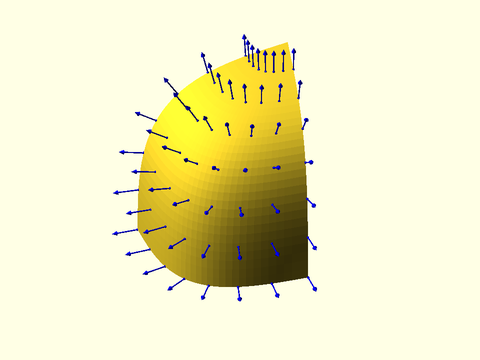
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
patch=[
repeat([-12.5, 12.5, 15],5),
[[-6.25, 11.25, 15], [-6.25, 8.75, 15], [-6.25, 6.25, 15], [-8.75, 6.25, 15], [-11.25, 6.25, 15]],
[[0, 10, 15], [0, 5, 15], [0, 0, 15], [-5, 0, 15], [-10, 0, 15]],
[[0, 10, 8.75], [0, 5, 8.75], [0, 0, 8.75], [-5, 0, 8.75], [-10, 0, 8.75]],
[[0, 10, 2.5], [0, 5, 2.5], [0, 0, 2.5], [-5, 0, 2.5], [-10, 0, 2.5]]
];
vnf_polyhedron(bezier_vnf(patch, 32));
uv = lerpn(0,1,8);
pts = bezier_patch_points(patch, uv, uv);
normals = bezier_patch_normals(patch, uv, uv);
for(i=idx(uv),j=idx(uv)){
if (is_def(normals[i][j]))
stroke([pts[i][j],pts[i][j]-2*normals[i][j]], width=0.1,
endcap1="dot",endcap2="arrow2",color="blue");
}
Example 4: This example has a singularities where the tangent lines don't exist, so the normal will be undef at those points.
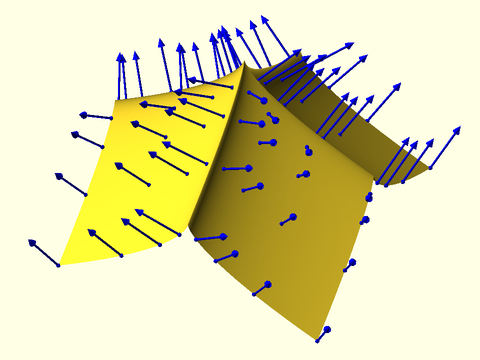
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
pts1 = [ [-5,0,0], [5,0,5], [-5,0,5], [5,0,0] ];
pts2 = [ [0,-5,0], [0,5,5], [0,-5,5], [0,5,0] ];
patch = [for(i=[0:3])
[for(j=[0:3]) pts1[i]+pts2[j] ] ];
vnf_polyhedron(bezier_vnf(patch, 163));
uv = [0,.1,.2,.3,.7,.8,.9,1];//lerpn(0,1,8);
pts = bezier_patch_points(patch, uv, uv);
normals = bezier_patch_normals(patch, uv, uv);
for(i=idx(uv),j=idx(uv))
stroke([pts[i][j],pts[i][j]+2*normals[i][j]], width=0.08,
endcap1="dot",endcap2="arrow2",color="blue");
Synopsis: Creates a thin sheet from a bezier patch by extruding in normal to the patch [VNF]
Topics: Bezier Patches
See Also: bezier_patch_normals(), vnf_sheet()
Description:
Constructs a thin sheet from a bezier patch by offsetting the given patch along the normal vectors to the patch surface. The thickness value must be small enough so that no points cross each other when the offset is computed, because that results in invalid geometry and will give rendering errors. Rendering errors may not manifest until you add other objects to your model. It is your responsibility to avoid invalid geometry!
The normals are computed using bezier_patch_normals() and if they are degenerate then
the computation will fail or produce incorrect results. See bezier_patch_normals() for
examples of various ways the normals can be degenerate.
When thickness is positive, the given bezier patch is extended towards its "inside", which is the side that appears purple in the "thrown together" view. You can extend the patch in the other direction using a negative thickness value.
Arguments:
| By Position | What it does |
|---|---|
patch |
bezier patch to process |
thickness |
amount to offset; can be positive or negative |
| By Name | What it does |
|---|---|
splinesteps |
Number of segments on the border edges of the bezier surface. You can specify [USTEPS,VSTEPS]. Default: 16 |
style |
vnf_vertex_array() style to use. Default: "default" |
Example 1:

include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
patch = [
// u=0,v=0 u=1,v=0
[[-50,-50, 0], [-16,-50, 20], [ 16,-50, -20], [50,-50, 0]],
[[-50,-16, 20], [-16,-16, 20], [ 16,-16, -20], [50,-16, 20]],
[[-50, 16, 20], [-16, 16, -20], [ 16, 16, 20], [50, 16, 20]],
[[-50, 50, 0], [-16, 50, -20], [ 16, 50, 20], [50, 50, 0]],
// u=0,v=1 u=1,v=1
];
vnf_polyhedron(bezier_sheet(patch, 10));
Synopsis: Shows a bezier path and its associated control points. [Geom]
Topics: Bezier Paths, Debugging
See Also: bezpath_curve()
Usage:
- debug_bezier(bez, [size], [N=]);
Description:
Renders 2D or 3D bezier paths and their associated control points to help debug bezier paths. The endpoints of each bezier curve in the bezier path are marked with a blue circle and the intermediate control points with a red plus sign. For cubic (degree 3) bezier paths, the module displays the standard representation of the control points as "handles" at each endpoint. For other degrees the control points are drawn as a polygon. You can of course give a single bezier curve as input, but you must in that case explicitly specify the bezier degree when it is not a cubic bezier.
Arguments:
| By Position | What it does |
|---|---|
bez |
the array of points in the bezier. |
size |
diameter of the lines drawn. |
| By Name | What it does |
|---|---|
N |
The degree of the bezier curves. Cubic beziers have N=3. Default: 3 |
Example 1: Cubic bezier path
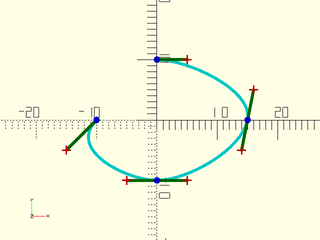
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bez = [
[-10, 0], [-15, -5],
[ -5, -10], [ 0, -10], [ 5, -10],
[ 14, -5], [ 15, 0], [16, 5],
[ 5, 10], [ 0, 10]
];
debug_bezier(bez, N=3, width=0.5);
Example 2: Quartic (degree 4) bezier path
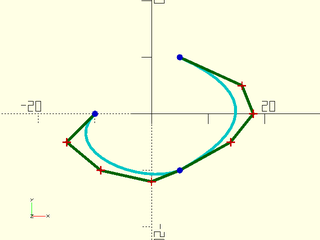
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
bez = [
[-10, 0], [-15, -5],
[ -9, -10], [ 0, -12], [ 5, -10],
[ 14, -5], [ 18, 0], [16, 5],
[ 5, 10]
];
debug_bezier(bez, N=4, width=0.5);
Synopsis: Shows a bezier surface patch and its associated control points. [Geom]
Topics: Bezier Patches, Debugging
See Also: bezier_patch_points(), bezier_patch_flat(), bezier_vnf()
Usage:
- debug_bezier_patches(patches, [size=], [splinesteps=], [showcps=], [showdots=], [showpatch=], [convexity=], [style=]);
Description:
Shows the surface, and optionally, control points of a list of bezier patches.
Arguments:
| By Position | What it does |
|---|---|
patches |
A list of rectangular bezier patches. |
| By Name | What it does |
|---|---|
splinesteps |
Number of segments to divide each bezier curve into. Default: 16 |
showcps |
If true, show the controlpoints as well as the surface. Default: true. |
showdots |
If true, shows the calculated surface vertices. Default: false. |
showpatch |
If true, shows the surface faces. Default: true. |
size |
Size to show control points and lines. Default: 1% of the maximum side length of a box bounding the patch. |
style |
The style of subdividing the quads into faces. Valid options are "default", "alt", and "quincunx". |
convexity |
Max number of times a line could intersect a wall of the shape. |
Example 1:
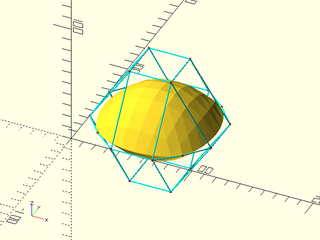
include <BOSL2/std.scad>
include <BOSL2/beziers.scad>
patch1 = [
[[15,15,0], [33, 0, 0], [ 67, 0, 0], [ 85, 15,0]],
[[ 0,33,0], [33, 33, 50], [ 67, 33, 50], [100, 33,0]],
[[ 0,67,0], [33, 67, 50], [ 67, 67, 50], [100, 67,0]],
[[15,85,0], [33,100, 0], [ 67,100, 0], [ 85, 85,0]],
];
patch2 = [
[[15,85,0], [33,100, 0], [ 67,100, 0], [ 85, 85,0]],
[[ 0,67,0], [33, 67,-50], [ 67, 67,-50], [100, 67,0]],
[[ 0,33,0], [33, 33,-50], [ 67, 33,-50], [100, 33,0]],
[[15,15,0], [33, 0, 0], [ 67, 0, 0], [ 85, 15,0]],
];
debug_bezier_patches(patches=[patch1, patch2], splinesteps=8, showcps=true);
Table of Contents
Function Index
Topics Index
Cheat Sheet
Tutorials
Basic Modeling:
- constants.scad STD
- transforms.scad STD
- attachments.scad STD
- shapes2d.scad STD
- shapes3d.scad STD
- drawing.scad STD
- masks2d.scad STD
- masks3d.scad STD
- distributors.scad STD
- color.scad STD
- partitions.scad STD
- miscellaneous.scad STD
Advanced Modeling:
- paths.scad STD
- regions.scad STD
- skin.scad STD
- vnf.scad STD
- beziers.scad
- nurbs.scad
- rounding.scad
- turtle3d.scad
Math:
- math.scad STD
- linalg.scad STD
- vectors.scad STD
- coords.scad STD
- geometry.scad STD
- trigonometry.scad STD
Data Management:
- version.scad STD
- comparisons.scad STD
- lists.scad STD
- utility.scad STD
- strings.scad STD
- structs.scad STD
- fnliterals.scad
Threaded Parts:
Parts:
- ball_bearings.scad
- cubetruss.scad
- gears.scad
- hinges.scad
- joiners.scad
- linear_bearings.scad
- modular_hose.scad
- nema_steppers.scad
- polyhedra.scad
- sliders.scad
- tripod_mounts.scad
- walls.scad
- wiring.scad
STD = Included in std.scad