Skip to content

Latest commit

 

History

History
99 lines (49 loc) · 3.17 KB

README_EN.md

File metadata and controls

99 lines (49 loc) · 3.17 KB
Raw

1724. Checking Existence of Edge Length Limited Paths II

中文文档

Description

An undirected graph of n nodes is defined by edgeList, where edgeList[i] = [ui, vi, disi] denotes an edge between nodes ui and vi with distance disi. Note that there may be multiple edges between two nodes, and the graph may not be connected.

Implement the DistanceLimitedPathsExist class:

    <li><code>DistanceLimitedPathsExist(int n, int[][] edgeList)</code> Initializes the class with an undirected graph.</li>

<li><code>boolean query(int p, int q, int limit)</code> Returns <code>true</code> if there exists a path from <code>p</code> to <code>q</code> such that each edge on the path has a distance <strong>strictly less than</strong> <code>limit</code>, and otherwise <code>false</code>.</li>

 

Example 1:

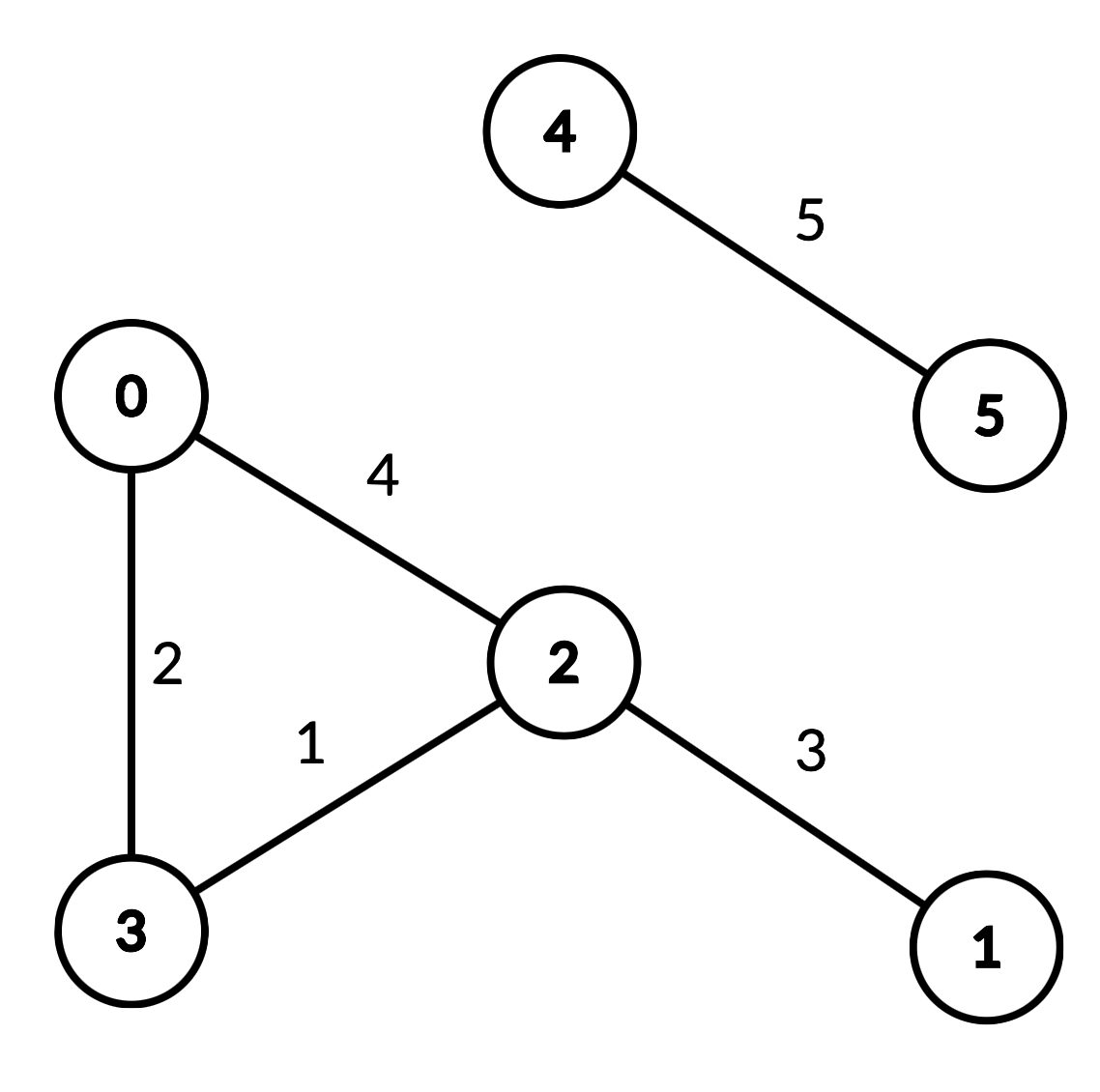
Input

["DistanceLimitedPathsExist", "query", "query", "query", "query"]

[[6, [[0, 2, 4], [0, 3, 2], [1, 2, 3], [2, 3, 1], [4, 5, 5]]], [2, 3, 2], [1, 3, 3], [2, 0, 3], [0, 5, 6]]

Output

[null, true, false, true, false]



Explanation

DistanceLimitedPathsExist distanceLimitedPathsExist = new DistanceLimitedPathsExist(6, [[0, 2, 4], [0, 3, 2], [1, 2, 3], [2, 3, 1], [4, 5, 5]]);

distanceLimitedPathsExist.query(2, 3, 2); // return true. There is an edge from 2 to 3 of distance 1, which is less than 2.

distanceLimitedPathsExist.query(1, 3, 3); // return false. There is no way to go from 1 to 3 with distances strictly less than 3.

distanceLimitedPathsExist.query(2, 0, 3); // return true. There is a way to go from 2 to 0 with distance < 3: travel from 2 to 3 to 0.

distanceLimitedPathsExist.query(0, 5, 6); // return false. There are no paths from 0 to 5.

 

Constraints:

    <li><code>2 &lt;= n &lt;= 10<sup>4</sup></code></li>

<li><code>0 &lt;= edgeList.length &lt;= 10<sup>4</sup></code></li>

<li><code>edgeList[i].length == 3</code></li>

<li><code>0 &lt;= u<sub>i</sub>, v<sub>i</sub>, p, q &lt;= n-1</code></li>

<li><code>u<sub>i</sub> != v<sub>i</sub></code></li>

<li><code>p != q</code></li>

<li><code>1 &lt;= dis<sub>i</sub>, limit &lt;= 10<sup>9</sup></code></li>

<li>At most&nbsp;<code>10<sup>4</sup></code> calls will be made to <code>query</code>.</li>

Solutions

Python3



Java




...