README.md

1724. 检查边长度限制的路径是否存在 II

English Version

题目描述

一张有 n 个节点的无向图以边的列表 edgeList 的形式定义，其中 edgeList[i] = [ui, vi, disi] 表示一条连接 ui 和 vi ，距离为 disi 的边。注意，同一对节点间可能有多条边，且该图可能不是连通的。

实现 DistanceLimitedPathsExist 类：

• DistanceLimitedPathsExist(int n, int[][] edgeList) 以给定的无向图初始化对象。
• boolean query(int p, int q, int limit) 当存在一条从 p 到 q 的路径，且路径中每条边的距离都严格小于 limit 时，返回 true ，否则返回 false 。

 

示例 1:

输入：
["DistanceLimitedPathsExist", "query", "query", "query", "query"]
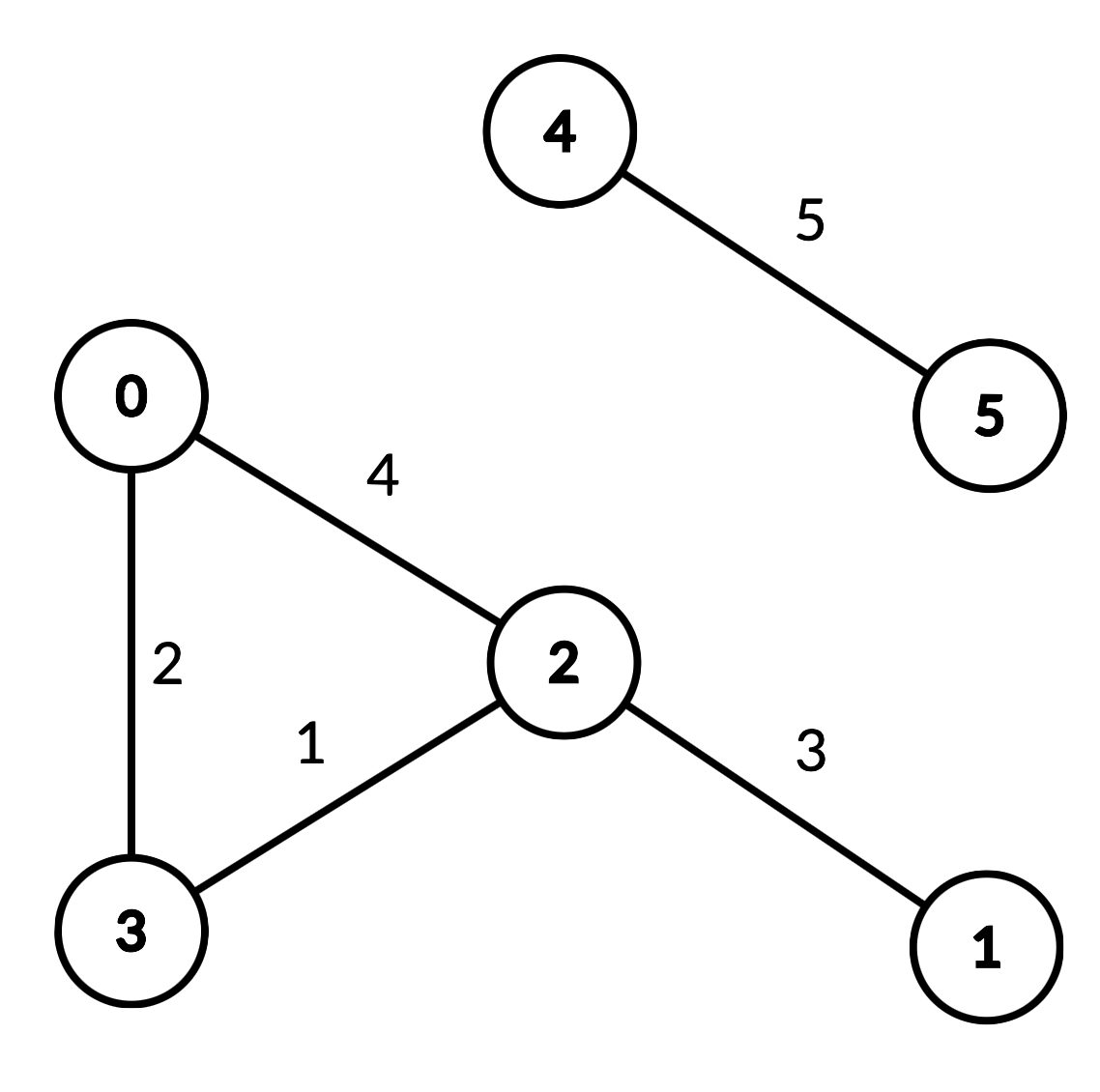
[[6, [[0, 2, 4], [0, 3, 2], [1, 2, 3], [2, 3, 1], [4, 5, 5]]], [2, 3, 2], [1, 3, 3], [2, 0, 3], [0, 5, 6]]
输出：
[null, true, false, true, false]

解释：
DistanceLimitedPathsExist distanceLimitedPathsExist = new DistanceLimitedPathsExist(6, [[0, 2, 4], [0, 3, 2], [1, 2, 3], [2, 3, 1], [4, 5, 5]]);
distanceLimitedPathsExist.query(2, 3, 2); // 返回 true。存在一条从 2 到 3 ，距离为 1 的边，
                                          // 这条边的距离小于 2。
distanceLimitedPathsExist.query(1, 3, 3); // 返回 false。从 1 到 3 之间不存在每条边的距离都
                                          // 严格小于 3 的路径。
distanceLimitedPathsExist.query(2, 0, 3); // 返回 true。存在一条从 2 到 0 的路径，使得每条边的
                                          // 距离 < 3：从 2 到 3 到 0 行进即可。
distanceLimitedPathsExist.query(0, 5, 6); // 返回 false。从 0 到 5 之间不存在路径。

 

提示：

• 2 <= n <= 104
• 0 <= edgeList.length <= 104
• edgeList[i].length == 3
• 0 <= ui, vi, p, q <= n-1
• ui != vi
• p != q
• 1 <= disi, limit <= 109
• 最多调用 104 次 query 。

解法

Python3

Java

...