equilibrium_slow_approach

Slow approach to equilibrium.

library(tree)

library(nleqslv)

library(rootSolve)

library(parallel)

source("equilibrium_fun.R")

Here's a situation where our equilibrium finding totally falls apart.

time_disturbance <- 2.5

pars <- list(c_r1=0.5, c_r2=0, B5=0, c_d1=1, B6=1)

p <- make_pars(pars, time_disturbance)

add_strategy(p, list(rho=5.1))

res <- equilibrium_seed_rain(p)

## 1: Splitting {13} times (92)
## 2: Splitting {15} times (105)
## 3: Splitting {9} times (120)
## 4: Splitting {1} times (129)
## 5: Splitting {1} times (130)
## 6: Splitting {1} times (131)
## *** 1: {1} -> {1.054} (delta = {0.05438})
## *** 2: {1.054} -> {1.112} (delta = {0.05725})
## *** 3: {1.112} -> {1.172} (delta = {0.06026})
## *** 4: {1.172} -> {1.235} (delta = {0.06342})
## *** 5: {1.235} -> {1.302} (delta = {0.06674})
## *** 6: {1.302} -> {1.372} (delta = {0.07021})
## *** 7: {1.372} -> {1.446} (delta = {0.07386})
## *** 8: {1.446} -> {1.524} (delta = {0.07767})
## *** 9: {1.524} -> {1.605} (delta = {0.08167})
## *** 10: {1.605} -> {1.691} (delta = {0.08585})
## *** 11: {1.691} -> {1.782} (delta = {0.09022})
## *** 12: {1.782} -> {1.876} (delta = {0.09479})
## *** 13: {1.876} -> {1.976} (delta = {0.09957})
## *** 14: {1.976} -> {2.08} (delta = {0.1046})
## *** 15: {2.08} -> {2.19} (delta = {0.1098})
## *** 16: {2.19} -> {2.305} (delta = {0.1152})
## *** 17: {2.305} -> {2.426} (delta = {0.1209})
## *** 18: {2.426} -> {2.553} (delta = {0.1268})
## *** 19: {2.553} -> {2.686} (delta = {0.1329})
## *** 20: {2.686} -> {2.825} (delta = {0.1393})

approach <- t(sapply(attr(res, "progress"), "[[", "seed_rain"))

r <- range(approach)

plot(approach, type="n", las=1, xlim=r, ylim=r)

abline(0, 1, lty=2, col="grey")

cobweb(approach, pch=19, cex=.5, type="o")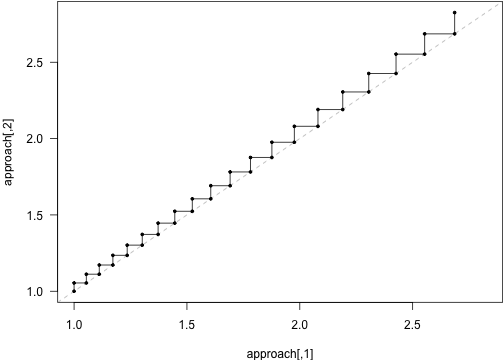

Case 1: single strategy, can exist at equilibrium:

f <- make_equilibrium_runner(p)

This nails it:

tol <- p$control$parameters$equilibrium_eps

maxit <- p$control$parameters$equilibrium_nsteps

control <- list(xtol=tol, ftol=tol, maxit=maxit)

sol <- nleqslv(p$seed_rain, make_target(f), global="none", control=control)

## seed_rain: 1, last: 1
## 1: Splitting {13} times (92)
## 2: Splitting {15} times (105)
## 3: Splitting {9} times (120)
## 4: Splitting {1} times (129)
## 5: Splitting {1} times (130)
## 6: Splitting {1} times (131)
## seed_rain: 1, last: 1
## seed_rain: 1, last: 1
## seed_rain: 38.4, last: 1
## 1: Splitting {13} times (92)
## 2: Splitting {15} times (105)
## 3: Splitting {8} times (120)
## 4: Splitting {1} times (128)
## 5: Splitting {1} times (129)
## seed_rain: 38.9, last: 38.4
## seed_rain: 38.9, last: 38.9

out <- f(sol$x)

## seed_rain: 38.9, last: 38.9

diff(as.numeric(out))

## [1] 2.138e-07

Or with multiroot:

sol_m <- multiroot(make_target(f), p$seed_rain, positive=TRUE)

## seed_rain: 1, last: 38.9
## 1: Splitting {13} times (92)
## 2: Splitting {15} times (105)
## 3: Splitting {9} times (120)
## 4: Splitting {1} times (129)
## 5: Splitting {1} times (130)
## 6: Splitting {1} times (131)
## seed_rain: 1, last: 1
## seed_rain: 1, last: 1
## seed_rain: 38.3, last: 1
## 1: Splitting {13} times (92)
## 2: Splitting {15} times (105)
## 3: Splitting {8} times (120)
## 4: Splitting {1} times (128)
## 5: Splitting {1} times (129)
## seed_rain: 38.3, last: 38.3
## seed_rain: 38.9, last: 38.3
## seed_rain: 38.9, last: 38.9
## seed_rain: 38.9, last: 38.9

Case 2: single strategy, cannot exist at equilibrium:

p2 <- make_pars(pars, time_disturbance)

add_strategy(p2, list(rho=4))

f2 <- make_equilibrium_runner(p2)

This one gets stuck, proposing a really negative value that we truncate and that's OK

sol2 <- nleqslv(p2$seed_rain, make_target(f2), global="none", control=control)

## seed_rain: 1, last: 1
## 1: Splitting {13} times (92)
## 2: Splitting {15} times (105)
## 3: Splitting {9} times (120)
## 4: Splitting {1} times (129)
## 5: Splitting {1} times (130)
## 6: Splitting {1} times (131)
## seed_rain: 1, last: 1
## seed_rain: 1, last: 1

multiroot actually does quite well here:

sol2_m <- multiroot(make_target(f2), p2$seed_rain, positive=TRUE)

## seed_rain: 1, last: 1
## seed_rain: 1, last: 1
## seed_rain: 1, last: 1
## seed_rain: 0, last: 1
## seed_rain: 1e-08, last: 0
## seed_rain: 0, last: 1e-08

Case 3: multiple strategies that displace each other:

p3 <- make_pars(pars, time_disturbance)

add_strategy(p3, list(rho=5.1))

add_strategy(p3, list(rho=5.102))

p3$seed_rain <- c(sol$x, 1)

f3 <- make_equilibrium_runner(p3)

This gets into a bit of a tangle, suggesting values that don't really make much sense. It makes really weird excursions because of the discontinuity at zero.

sol3 <- nleqslv(p3$seed_rain, make_target(f3), global="none", control=control)

## seed_rain: 38.9, 1, last: 38.9, 1
## 1: Splitting {13,3} times (92,92)
## 2: Splitting {15,0} times (105,95)
## 3: Splitting {8,0} times (120,95)
## 4: Splitting {1,0} times (128,95)
## 5: Splitting {1,0} times (129,95)
## seed_rain: 38.9, 1, last: 38.9, 1
## seed_rain: 38.9, 1, last: 38.9, 1
## seed_rain: 38.9, 1, last: 38.9, 1
## seed_rain: 7024, 0, last: 38.9, 1
## 1: Splitting {14,0} times (92,92)
## 2: Splitting {15,0} times (106,92)
## 3: Splitting {12,0} times (121,92)
## seed_rain: 29.3, 13.2, last: 7024, 0
## 1: Splitting {12,11} times (92,92)
## 2: Splitting {14,8} times (104,103)
## 3: Splitting {6,2} times (118,111)
## 4: Splitting {1,1} times (124,113)
## 5: Splitting {1,0} times (125,114)
## seed_rain: 24.3, 15.7, last: 29.3, 13.2
## 1: Splitting {0,3} times (126,114)
## seed_rain: 0.884, 39.6, last: 24.3, 15.7
## 1: Splitting {3,13} times (92,92)
## 2: Splitting {0,15} times (95,105)
## 3: Splitting {0,8} times (95,120)
## 4: Splitting {0,1} times (95,128)
## 5: Splitting {0,1} times (95,129)
## seed_rain: 15, 24.6, last: 0.884, 39.6
## 1: Splitting {12,12} times (92,92)
## 2: Splitting {13,13} times (104,104)
## 3: Splitting {5,5} times (117,117)
## 4: Splitting {1,1} times (122,122)
## 5: Splitting {0,1} times (123,123)
## seed_rain: 10.5, 29, last: 15, 24.6
## seed_rain: 0, 483, last: 10.5, 29
## 1: Splitting {0,13} times (92,92)
## 2: Splitting {0,14} times (92,105)
## 3: Splitting {0,3} times (92,119)
## seed_rain: 9.46, 29.4, last: 0, 483
## 1: Splitting {8,12} times (92,92)
## 2: Splitting {5,15} times (100,104)
## 3: Splitting {1,7} times (105,119)
## 4: Splitting {0,2} times (106,126)
## 5: Splitting {0,1} times (106,128)
## seed_rain: 10, 29.6, last: 9.46, 29.4
## seed_rain: 10.1, 29.5, last: 10, 29.6
## seed_rain: 5.05, 34.5, last: 10.1, 29.5
## seed_rain: 463, 0, last: 5.05, 34.5
## 1: Splitting {13,0} times (92,92)
## 2: Splitting {14,0} times (105,92)
## 3: Splitting {3,0} times (119,92)
## seed_rain: 5.15, 34.3, last: 463, 0
## 1: Splitting {7,13} times (92,92)
## 2: Splitting {4,15} times (99,105)
## 3: Splitting {1,8} times (103,120)
## 4: Splitting {0,1} times (104,128)
## 5: Splitting {0,1} times (104,129)
## seed_rain: 5.4, 34.1, last: 5.15, 34.3
## seed_rain: 0, 232, last: 5.4, 34.1
## 1: Splitting {0,13} times (92,92)
## 2: Splitting {0,15} times (92,105)
## 3: Splitting {0,6} times (92,120)
## 4: Splitting {0,1} times (92,126)
## seed_rain: 5.72, 33.9, last: 0, 232
## 1: Splitting {7,13} times (92,92)
## 2: Splitting {5,15} times (99,105)
## 3: Splitting {1,8} times (104,120)
## 4: Splitting {0,1} times (105,128)
## 5: Splitting {0,1} times (105,129)
## seed_rain: 5.92, 33.7, last: 5.72, 33.9
## seed_rain: 0, 309, last: 5.92, 33.7
## 1: Splitting {0,13} times (92,92)
## 2: Splitting {0,15} times (92,105)
## 3: Splitting {0,4} times (92,120)
## 4: Splitting {0,1} times (92,124)
## seed_rain: 6.13, 33.5, last: 0, 309
## 1: Splitting {7,13} times (92,92)
## 2: Splitting {5,15} times (99,105)
## 3: Splitting {1,8} times (104,120)
## 4: Splitting {0,1} times (105,128)
## 5: Splitting {0,1} times (105,129)
## seed_rain: 6.35, 33.3, last: 6.13, 33.5

This gets tangled, then jumps to (0,0)

sol3_m <- multiroot(make_target(f3), p3$seed_rain, positive=TRUE)

## seed_rain: 38.9, 1, last: 6.35, 33.3
## 1: Splitting {13,3} times (92,92)
## 2: Splitting {15,0} times (105,95)
## 3: Splitting {8,0} times (120,95)
## 4: Splitting {1,0} times (128,95)
## 5: Splitting {1,0} times (129,95)
## seed_rain: 38.9, 1, last: 38.9, 1
## seed_rain: 38.9, 1, last: 38.9, 1
## seed_rain: 38.9, 1, last: 38.9, 1
## seed_rain: 1295, 0, last: 38.9, 1
## 1: Splitting {16,0} times (92,92)
## 2: Splitting {11,0} times (108,92)
## 3: Splitting {1,0} times (119,92)
## seed_rain: 1295, 0, last: 1295, 0
## seed_rain: 1295, 1e-08, last: 1295, 0
## seed_rain: 0, 0, last: 1295, 1e-08
## seed_rain: 0, 0, last: 0, 0