-
Notifications
You must be signed in to change notification settings - Fork 29
Dev: 4. Storage Whitepaper
Asami is a flexible database which may be used in web pages, or services, but in both configurations, it stores data in active memory. While fast, this limits the size of the data that Asami can manage and limits the lifespan of the data to the running time of the application.
This paper introduces the Asami Durability Layer to address these issues. This design is derived from experience designing the storage layer in the open source Mulgara database.
Asami graphs are defined as a series of “triples”, or a statement with three elements. These are used to describe a directed graph, which can be visualized as a collection of nodes, which are connected by arrows.
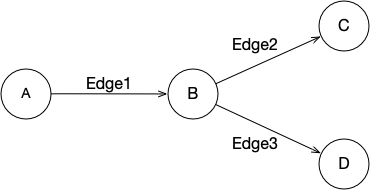
This simple graph can be stored as the set of triples:
A Edge1 B
B Edge2 C
B Edge3 D
To store these statements in a useful way, Asami uses an index. This allows all statements to be found quickly and easily, based on any value in any column. Indexes like this are trivial to implement in active memory but require more planning when using long-term storage.
The general purpose of an index is to make it quick and easy to find required data. The most common way of doing this is to create a structure that sorts the data or can provide a mechanism for sorting the data.
Asami’s indexes will be sorting each triple in several ways:
- By first column, then second column, then third column.
- By second column, then third column, then first column.
- By third column, then first column, then second first column.
This combination of indexes allows triples to be found quickly, by any combination of values in any column.
The most common way to build indexes that sort data is with a data tree. These structures allow data to be inserted into them in any order, naturally sorting the data as they go.
Trees are built out of data elements that are consistently sized, which makes them easy to store and retrieve in persistent storage, such as a disk. However, a lot of data is very inconsistent in size, meaning that other structures are also necessary.
Most data in Asami, including trees, will be built using a data abstraction called a Block. This is simply a set of bytes, of a consistent size, which can be stored durably. The block API includes functions for reading and writing various data types into specific byte positions inside the block.
Every block will have a numeric identifier, and data in the block will be found by an offset within the block. Combining a block identifier and the offset provides a 64-bit number, which will be the basis of storing and retrieving all data in Asami. The architecture of Asami also requires that blocks only be written to storage a single time.
The benefit to using blocks as a storage abstraction is that they can be implemented over various persistence APIs, without modifying the higher levels of data management. Examples of APIs for implementing blocks include:
- Disk Files
- IndexedDB in web browsers
- S3 Buckets
- RDBMS systems
The initial implementations for Asami blocks are in Memory Mapped Files and IndexedDB.
To keep triples a consistent size for storing in blocks, all triples will be stored as a set of 3 numbers. Each number will then be used to reference the actual data for that position in the triple. This requires an index that can convert from numbers back into the data that they reference, as well as a mechanism for finding existing data to find the associated number. The structure for managing this two-way mapping is called the Data Pool.
As data, such as strings and URIs are loaded into Asami, they will be stored in the Data Pool. Each datum will be serialized into bytes and stored in a block. The block number and offset for this data forms the 64-bit identifier that will be used to represent that datum in the triples.
In some cases, it may be necessary to have large individual items of data stored in multiple blocks. In this case, the serialization will need to refer to following blocks so that the datum can be chained together. Alternately, some storage media (such as disk files) can allow data to be packed tightly without blocks, with just the 64-bit file offset providing access to the stored data.
Once a datum has been stored and associated with an ID that can be used to retrieve it, it must also be stored in an indexing tree. Nodes in a tree all have an identical size, so rather than containing all of the datum, they will contain the assigned ID for the datum, which serves as a pointer to the datum, along with a header. The header is simply a small amount of information from the data that will allow for fast traversal of the tree without needing to retrieve all of the data from the associated block. For instance, a string entry will contain the ID for the string (allowing the entire string to be retrieved), as well as the first few characters of the string, so that it can be quickly checked at a course level for alphabetical ordering.
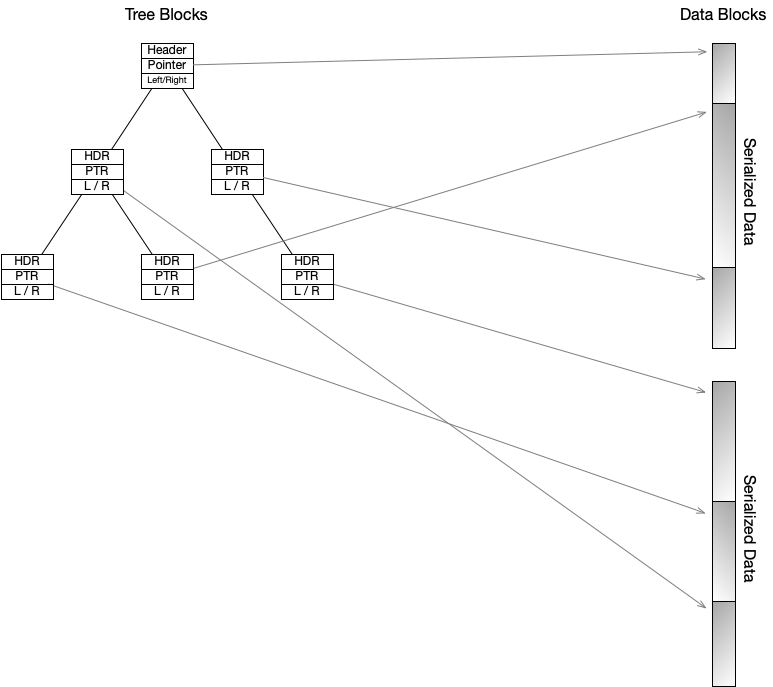
The diagram here shows a binary tree, which means that datum can be found by searching the tree, going left or right, according to comparison order. Once found, the pointer is the ID for that datum. Going the other way, an ID refers directly to the serialized form of the datum. The choice of binary tree will be justified later.
With each element of a triple being mapped to an ID, triples can be stored as a set of numbers. For instance, the example earlier might be stored as:
| Original | Serialized |
|---|---|
| A Edge1 B | 1 2 3 |
| B Edge2 C | 3 4 5 |
| B Edge3 D | 3 6 7 |
While this example has nodes represented by a single letter, most elements are made up of long strings and URIs, meaning that the space saving of using numbers is significant. More importantly, it ensures that triples are always a consistent size, and that comparison between triples is always fast. The actual serialization of a triple will include a fourth number which contains metadata about the triple. This will be a 64-bit number that is split into a unique ID for each triple (40 bits, or 1 trillion triples), as well as a transaction number to indicate when the triple was created (24 bits, or 16 million transactions).
As described earlier, indexing triples requires ordering the triples, which will be accomplished by using trees. However, placing a single triple per tree node would be prohibitively expensive in space overhead. It would also result in a large number of block retrievals, which will result in a much slower system. To avoid this, each node of the indexing tree will reference a unique block that contains up to 256 triples. This results in blocks of 8kB, though this specific limit is expected to be configurable.
Choosing the block size provides a balance between blocks that are too small, and result in more block accesses, and blocks that are too large, which results in significant unused space. 8kB is a common logical block size for hard disk controllers, which is the minimum amount of data that can be read or written to a disk. This improves efficiency both for disk-based storage, and some other storage implementations which will ultimately store data on a disk as well.
A triple block represents a linear series of the 4 numbers that store a triple (remembering that the 4th element is for metadata). This means that each triple takes 32 bytes.
Finding triples in a block can be done via a binary search. Insertions are performed by finding the insertion point, moving all the triples to the end of the block up by 32 bytes, and then writing into the new space. Insertion into a block that is already full will split the block into two blocks, with each containing half of the original data.
One reason for keeping the maximum size of blocks small is to ensure that insertions can be confined to a small block of memory, and ideally a small write to disk.
Each triple block will be referenced by a node in an indexing tree. These nodes will contain the ID of the triple block, the number of triples in that block, and the smallest and largest triple to be found in the block. The 4th element of the triples can be avoided for these min/max triples, so the total space will be 8 numbers: ID + number-of-triples + 3 + 3
The number of triples can be stored in a single byte, since it cannot be larger than 256 (and will never be 0), however this would create misaligned blocks, which are slower to access. Also, a configurable block size may choose a value greater than 256, which would also require the number to be larger than a single byte.
Once each node in the tree has been paired with a block, it forms each of the 3 instances of the triples indexes.
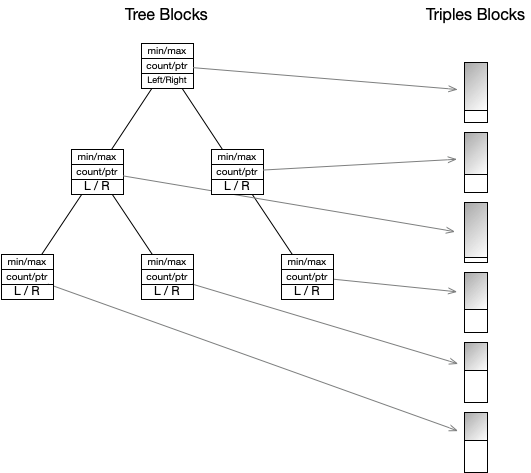
In order to make the data scale better, particularly over cloud services, blocks that are created and persisted to storage, will not be modified again. This is achieved through the tree structures that organize the data, since all blocks are reachable through trees.
When a node in a tree is modified, then instead of changing that node a copy is made instead. Because it is a copy, it will refer to the same children (if any) which remain unchanged. The parent of this node must also be copied but will be updated to refer to the new node, rather than the original, unmodified child node. This continues all the way to the root of the tree. The final state is to have 2 separate tree roots, which means 2 separate trees. The newer tree will have a single branch that has new nodes, and the rest of the tree will be shared with the original tree.
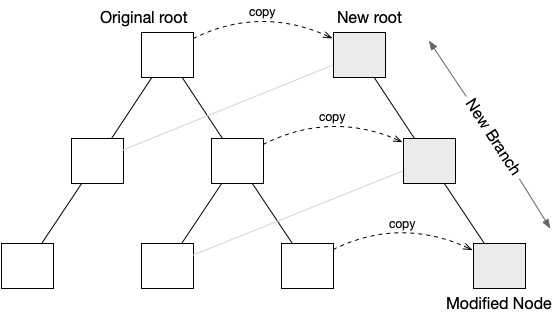
Modifications rarely happen in isolation, and multiple changes will typically be grouped to form a transaction. Each transaction will create its own new root, as above, with the data in committed to the transaction being accessible in the new tree. After the first modification, additional changes in the same transaction do not need to create their own branch. Instead, they will copy the appropriate node from the tree, and start iterating through parent nodes creating copies for the new transaction. As soon as a node is found to already be in the new transaction, then the iterations of copying to the root can stop.
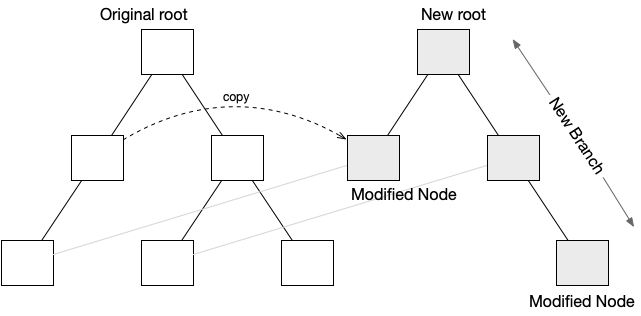
In this way, the original tree remains completely untouched, and cannot be corrupted. Adopting the new root as the latest committed transaction is an atomic operation, which means that the entire transaction either succeeds, or else can be abandoned. This avoids any possibility of corrupting existing data.
The data pool is cumulative and need not change at any point. Therefore, the only changes that need be recorded are in the triples indexes.
When triples need to be inserted or removed, the block that they are stored in will be updated, which will require the original block to be copied, just as for the tree updates above. Similarly, the tree node pointing to the block will need to be updated, leading to a new branch to the root of the tree.
A key difference here is that only the directly modified tree nodes will require new blocks to refer to. The remaining tree nodes in the branch can continue to point to the shared blocks from the committed tree.
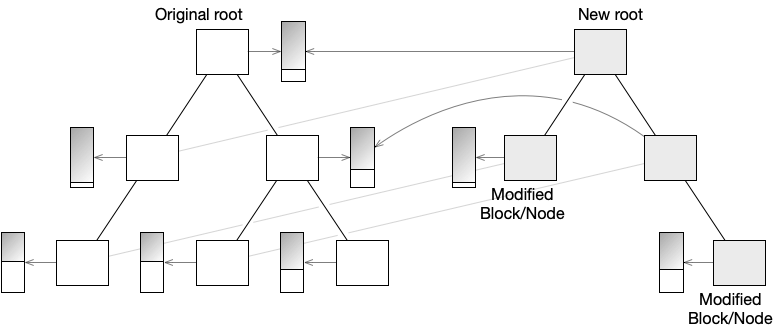
The diagram above shows the same tree from the previous section, with associated triple blocks. Note that only the modified nodes have new blocks which can be modified, while the other new nodes in the branch refer to the original, unmodified blocks.
It should be clear that any modifications to shared triple blocks would result in a new copy that belongs to the new transaction branch, but that the associated tree node would not need to be copied into the branch since it is already there.
Identifying which transaction a block belongs to could be done by adding an ID value to each block in storage. However, this uses space and shifts the even alignment of triples. Instead, this information can be found by exploiting the property of monotonically increasing block IDs. Block managers will always have a next-id value to allocate the ID of the next new block. They will also hold the ID that this value held at the beginning of a transaction, in order to roll back to it. Any block with an ID equal to or exceeding this rollback value will have been allocated in the current transaction.
Unlike the triples indexes, the data pool does not need to be updated. Once a string or other resource exists, it will never be modified. If a different string is required, then a different resource is created. This also applies to URIs, date-times, keywords, and more. As a result, transactions mean a lot less to the data pool. The one place where transactions may be of significance is during the transaction itself. If something goes wrong and the transaction should be rolled back, then the allocated data blocks may be truncated back to the state at the beginning of the transaction. This means that the new structure and root of the tree is removed, as is any new serialized data. Otherwise, a commit operation is the standard atomic operation which guarantees that the index is always in a fully consistent state.
All of the above examples show binary trees, which are not a common standard for database implementations. The particular binary tree implementation for Asami is an AVL Tree. This was chosen for a few reasons.
AVL Trees have the unusual property of having O(1), or constant-time complexity when inserting nodes. This is an important property for write operations, as storage I/O is the most expensive operation in any database. This factor alone make the AVL Tree a consideration, but interaction with the described structure has several benefits.
Read operations require log2(n) read operations, which is strictly not as good as the logb(n) operations required for trees with b-way branching, but this difference is actually a constant factor, and is therefore dropped from complexity calculations. Other scaling effects quickly overtake any observable differences. Note that the linear scaling effect is offset by a similar linear scaling effect of storing up to 128 triples per node.
The common multi-branch tree implementation is usually one of several variations of the B-tree. These trees store the data within the tree node, with child pointers occurring between the data nodes. While each data point could be a reference to a triple-block, the copy-on-write operations described in this document will require copying much more unrelated data for each transaction, which will cost more in storage and time.
Finally, the small size of the AVL nodes compared to B-tree nodes makes new branches lightweight, and often appearing in a single unit of storage access (such as disk blocks). The consecutive allocation of nodes in a transaction ensures that any branch created in a transaction will have good data locality. The smaller AVL nodes also means that memory and/or cache will hold far more nodes from the top layers of the tree than would be the case in a B-Tree, leading to similar performance in cached tree performance.
An important design consideration for any database is data locality. This means that data referring to related elements should be stored as close together as possible.
This tree/block design achieves data locality through 3 different mechanisms.
- Triple blocks store related triples in the same block together.
- Blocks are allocated sequentially during transactions.
- AVL Tree transaction branches ensure new nodes create branches whose blocks are immediately next to each other.
The most common pattern for triples is a series of attribute/value pairs for a single entity. These are always stored in a group in the SPO index due to natural ordering. On the rare occasion when they are split across two blocks, the blocks will have been allocated sequentially, and the data is therefore next to each other. This ensures that retrieval of an entire entity does not require reading from scattered blocks.
Similarly, finding entity via attribute/value pairs is done through a single lookup in the POS index, which will find all entity identifiers with those values in a group. The next step is often to read the entire entity, which was the process just described.
This set of indexes has a record of working quickly and effectively (see Mulgara) but the further grouping of triples in blocks assists in finding groups of related triples with minimal further access to storage.
As transactions progress, they require new blocks both to expand storage, and to perform copy-on-write operations for existing blocks. These blocks are allocated sequentially from storage. This means that all data in a transaction will be local to each other. This applies to both tree blocks and associated data blocks.
New nodes in an AVL tree always appear in the leaf positions, which may make them appear distantly removed in a tree diagram, but this perspective can be deceptive.
When a node is added to the leaf position of a tree, the entire branch leading to that node will be duplicated. Blocks which are allocated sequentially like this will be sequential in storage, as described in the previous section. This means that many searches for data are likely to be along paths of tree nodes that are stored consecutively. Over time, as new branches are formed in transactions, the first few elements of these branches will start to fragment, but these are at the top of the tree and consequently are normally available in memory.
The Asami storage layer is to be implemented with 4 indexes. Three indexes will be permutations of the triples, and the final index will store arbitrary data elements, such as strings and URIs.
All the storage will be built over a “Block” abstraction which allows isolation of platform specific code, both between the JVM and JavaScript platforms, and using arbitrary storage mechanisms. This provides a lot of flexibility for scaling, distribution, and redundancy. Data is all written to storage once, and never modified. This provides reliability and consistency, while also providing a full history for the database.