-
-
Notifications
You must be signed in to change notification settings - Fork 344
Domino Shuffling Algorithm Animation
The following picture shows an Aztec diamond graph of order 10:
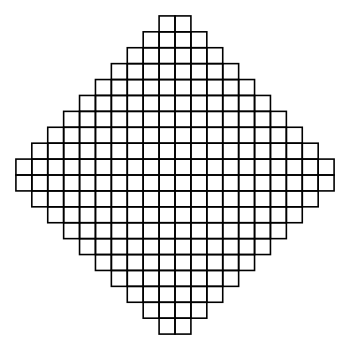
You can see from the top row to the bottom row, there are
2, 4, ..., 20, 20, ..., 4, 2
unit squares piled up layers by layers.
In general an Aztec diamond graph of order n (denoted as AZ(n) for short) is obtained via this way by piling up
2, 4, ..., 2*n, 2*n, ..., 4, 2
unit squares.
Now we consider domino tilings of AZ(n), i.e. tilings of AZ(n) with 1x2 dominoes. The following image shows one possible tiling of AZ(10):
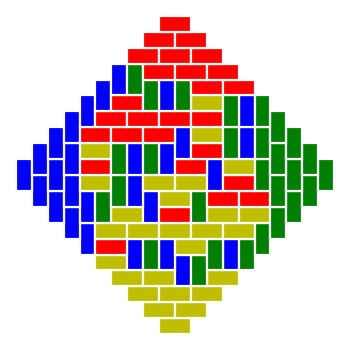
Our question is:
Question 1: How many domino tilings of
AZ(n)are there?
This problem seems quite innocent at the first glance: anyone with a high school level can understand it, but unfortunately all solutions known today (there are more than one dozen solutions) are not elementary: they either use quite sophisticated math, or requre quite genius insights.
The answer is 2**(n(n+1)/2), a short and neat expression which suggests it should also have a neat and beautiful solution, and it does. This solution is called the domino shuffling algorithm we implement here.
Before we state the algorithm, let's step further to another question:
Question 2: How to choose a random tiling among all these
2**(n(n+1)/2)tilings with uniform probability?
Compare this question with the Wilson algorithm animation in this repo, basically both of them are devised to do the same thing: sample with uniform probability from a very very large set (in fact they can be generalized to sample under any given probability distribution). For n=100, AZ(100) has 2**(5050) different tilings, far more large than the number of partices in the universe!
Domino Shuffling Algorithm Think the plane as an infinite chessboard, put
AZ(n)at the origin, the chessboard are colored in the fashion that the leftmost cell in the top row ofAZ(n)in white.A 2x2 block in called 'black', if the topleft cell in this block is black, and it's called 'bad' if it's black and it contains a pair of parellel dominoes.
The algo runs as follows: Suppose we are given a tiling
TofAZ(n-1), do
Find all bad blocks in
T, remove all the pairs of dominoes in them.For each domino
dthat remains inT, movedone step according to its orientation. The orientation of a dominodis determined by the following rule: find the unique 2x2 black blockBthat containsd, movedto the oppsite position inB.It can be proven that after the moves the holes can be filled up by disjoint 2x2 black blocks in a unique way (this assertion is the crux of this algo), we use either a pair of horizontal or vertical dominoes to tile each block.
Then one get a domino tiling
T'ofAZ(n). Further more, ifTis sampled from tilings ofAZ(n-1)with uniform probability, thenT'is also sampled from tilings ofAZ(n)with uniform probability.
The proof of this algo is highly non-trivial and one may refer to the two papers by Elkies, etc. and Propp for more details.
The gif below illustrates how this algo works:

You can see that it firstly generates a random tiling of AZ(1) (AZ(1) is simply a 2x2 square which has only two tilings, one can toss a coin to sample one), and then repeats the process "delete bad blocks" -- "move remaining dominoes" -- "fill up the holes". In each round (say round i) it builds a perfectly random tiling of AZ(i).
Once you understand the algo the code becomes quite straight-forward. There are a few traps one should be aware of: one must start the search from the boundary when deleting or filling the blocks.
There are two files aztec.py and aztec_matplotlib.py. They do the same job (random sampling) but one uses cairo for drawing and the other uses matplotlib. cairo is much faster than matplotlib but the latter renders better and much smaller images. So I used cairo to generate GIF animations and matplotlib to draw perfectly random tilings.