Concepts

UOST relies on the hypothesis that any mesh can be considered as a set of polygons, called cells, and that the model estimates the average value of the unknowns in each cell. Given a cell (let us call it A, Figure 1ab) UOST estimates, for each spectral component, the effect of a) the unresolved features located in A (Local Dissipation, LD); b) the unresolved features located upstream of A, and projecting their shadow on A (Shadow Effect, SE). For the estimation of SE, an upstream polygon A' is defined for each cell/spectral component, as the intersection between the joint cells neighboring A (cells B, C and D in figure Figure 1ab), and the flux upstream of A. For each cell or upstream polygon, and for each spectral component, two different transparency coefficients are estimated.

1. The overall transparency coefficient α, computed from the ratio between the cross section of the obstacles and the one of the cell containing them (Figure 1cd); and
2. a layout-dependent transparency β, defined as the average transparency of cell sections starting from the cell upstream side.

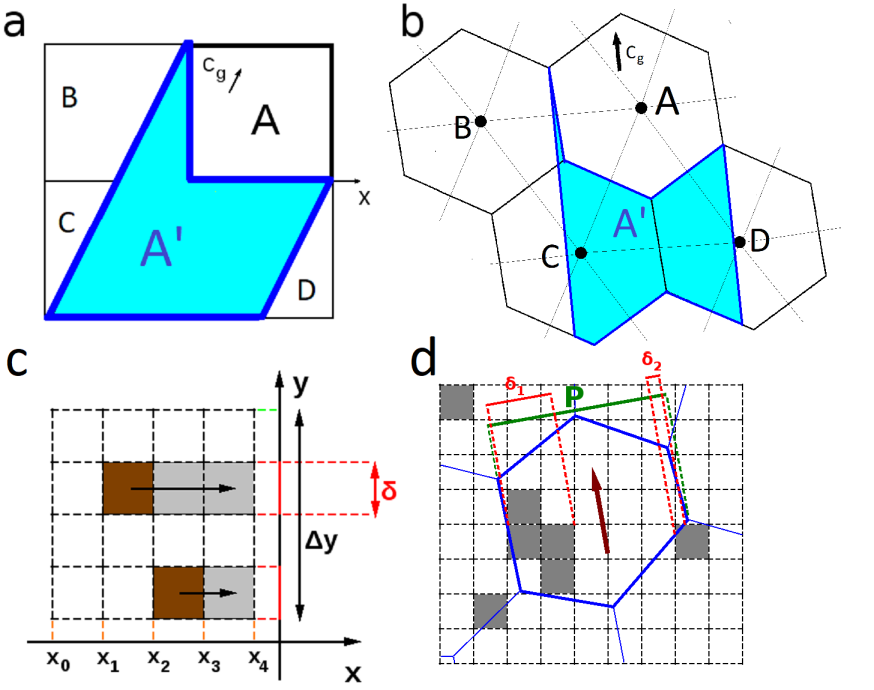Figure 1, a: a square cell (A) and its upstream polygon (A', delimited by blue line, in light blue color) for a spectral component propagating with group velocity c_g. The joint BCD polygon represents the neighborhood polygon. b: same as a, but for a triangular mesh (the hexagons approximate the median dual cells). c: Computation of α and β for a square cell, and a spectral component propagating along the x axis. d: Like c, but for a hexagonal cell and for a tilted spectral component. In panel d he gray squares represent unresolved obstacles.

An important limitation of UOST, is that to work properly on a given cell, it needs a time step of application of the source terms (in WW3 the global time step) lower than or equal to the critical CFL time step of the cell, i.e., the amount of time needed by the fastest spectral component to entirely cross the cell. Otherwise, part of the energy will leak through the cell without being blocked.

For a more exhaustive explanation of the UOST approach, the reader is referred to (Mentaschi et al., 2018a, 2015).

References

Mentaschi, L., Pérez, J., Besio, G., Mendez, F. J., & Menendez, M. (2015). Parameterization of unresolved obstacles in wave modelling: A source term approach. Ocean Modelling, 96, 93-102.

Mentaschi, L., Kakoulaki, G., Vousdoukas, M., Voukouvalas, E., Feyen, L., & Besio, G. (2018). Parameterizing unresolved obstacles with source terms in wave modeling: A real-world application. Ocean Modelling, 126, 77-84.