README.md

1819. 序列中不同最大公约数的数目

English Version

题目描述

给你一个由正整数组成的数组 nums 。

数字序列的 最大公约数 定义为序列中所有整数的共有约数中的最大整数。

• 例如，序列 [4,6,16] 的最大公约数是 2 。

数组的一个 子序列 本质是一个序列，可以通过删除数组中的某些元素（或者不删除）得到。

• 例如，[2,5,10] 是 [1,2,1,2,4,1,5,10] 的一个子序列。

计算并返回 nums 的所有 非空 子序列中 不同 最大公约数的 数目 。

 

示例 1：

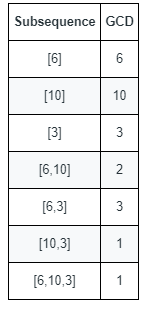
输入：nums = [6,10,3]
输出：5
解释：上图显示了所有的非空子序列与各自的最大公约数。
不同的最大公约数为 6 、10 、3 、2 和 1 。

示例 2：

输入：nums = [5,15,40,5,6]
输出：7

 

提示：

• 1 <= nums.length <= 105
• 1 <= nums[i] <= 2 * 105

解法

方法一：枚举 + 数学

对于数组 $nums$ 的所有子序列，其最大公约数一定不超过数组中的最大值 $mx$。

因此我们可以枚举 $[1,.. mx]$ 中的每个数 $x$，判断 $x$ 是否为数组 $nums$ 的子序列的最大公约数，如果是，则答案加一。

那么问题转换为：判断 $x$ 是否为数组 $nums$ 的子序列的最大公约数。我们可以通过枚举 $x$ 的倍数 $y$，判断 $y$ 是否在数组 $nums$ 中，如果 $y$ 在数组 $nums$ 中，则计算 $y$ 的最大公约数 $g$，如果出现 $g = x$，则 $x$ 是数组 $nums$ 的子序列的最大公约数。

时间复杂度 $O(n + M \times \log M)$，空间复杂度 $O(M)$。其中 $n$ 和 $M$ 分别是数组 $nums$ 的长度和数组 $nums$ 中的最大值。

Python3

class Solution:
    def countDifferentSubsequenceGCDs(self, nums: List[int]) -> int:
        mx = max(nums)
        vis = set(nums)
        ans = 0
        for x in range(1, mx + 1):
            g = 0
            for y in range(x, mx + 1, x):
                if y in vis:
                    g = gcd(g, y)
                    if g == x:
                        ans += 1
                        break
        return ans

Java

class Solution {
    public int countDifferentSubsequenceGCDs(int[] nums) {
        int mx = Arrays.stream(nums).max().getAsInt();
        boolean[] vis = new boolean[mx + 1];
        for (int x : nums) {
            vis[x] = true;
        }
        int ans = 0;
        for (int x = 1; x <= mx; ++x) {
            int g = 0;
            for (int y = x; y <= mx; y += x) {
                if (vis[y]) {
                    g = gcd(g, y);
                    if (x == g) {
                        ++ans;
                        break;
                    }
                }
            }
        }
        return ans;
    }

    private int gcd(int a, int b) {
        return b == 0 ? a : gcd(b, a % b);
    }
}

C++

class Solution {
public:
    int countDifferentSubsequenceGCDs(vector<int>& nums) {
        int mx = *max_element(nums.begin(), nums.end());
        vector<bool> vis(mx + 1);
        for (int& x : nums) {
            vis[x] = true;
        }
        int ans = 0;
        for (int x = 1; x <= mx; ++x) {
            int g = 0;
            for (int y = x; y <= mx; y += x) {
                if (vis[y]) {
                    g = gcd(g, y);
                    if (g == x) {
                        ++ans;
                        break;
                    }
                }
            }
        }
        return ans;
    }
};

Go

func countDifferentSubsequenceGCDs(nums []int) (ans int) {
	mx := 0
	for _, x := range nums {
		mx = max(mx, x)
	}
	vis := make([]bool, mx+1)
	for _, x := range nums {
		vis[x] = true
	}
	for x := 1; x <= mx; x++ {
		g := 0
		for y := x; y <= mx; y += x {
			if vis[y] {
				g = gcd(g, y)
				if g == x {
					ans++
					break
				}
			}
		}
	}
	return
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

func gcd(a, b int) int {
	if b == 0 {
		return a
	}
	return gcd(b, a%b)
}

...