This software creates an interactive webpage of college football probabilities using odds and lines from several online betting markets:
I also created an ensemble set of probabilities using a simple average of the probabilities from these four online markets.
Although there are several ways for bookies to express bets, the four markets I draw on use moneylines and fractional odds. In this section, I explain how to derive probabilities from both.
Moneyline odds (sometimes called "American odds") often appear as a single number with a magnitude in the hundreds (e.g. -110, +200, +250). If the moneyline is a negative number, the gamber has to bet that much to win $100. If the moneyline is positive, that is the amount the gamber can win if he bets $100.
Assume that the market price includes all information so it is impossible to beat the market and that betters are risk neutral (so losing a dollar hurts as much as getting a dollar helps). Then the expected value of the bet is zero.
Represent the moneyline by x and the probability by p. Then
| if x < 0 | if x > 0 |
|---|---|
| E[bet] = 0 | E[bet] = 0 |
| E[100p + x(1-p) ] = 0 | E[xp - 100(1-p) ] = 0 |
| 100 E(p) + x - x E(p) = 0 | x E(p) - 100 + 100 E(p) = 0 |
| E(p) = -x / (100 - x) | E(p) = 100 / (100 + x) |
South Carolina (the negative number) is favored over Texas A&M (the positive number). The probability that South Carolina wins is 400 / (100 + 400) = 0.8, and the probability that Texas A&M wins is 100 / (100 + 325) = 0.24.
Note that those probabilities sum to more than 1. That extra is the vig. Remove the vig by dividing each probability by the sum of the probabilities. In the above case, South Carolina's probability is 0.77 and Texas A&M's is 0.23.
Fractional odds appear as a fraction. The top is the number of dollars the better can win if he bets the bottom number of dollars. Again assume risk neutrality and a fully informed market. With fractional odds of x / y, then
| E[bet] = 0 |
|---|
| E[xp - y(1-p)] = 0 |
| x E(p) - y + y E(p) = 0 |
| E(p) = y / (x + y) |
Here are the fractional odds for the same South Carolina-Texas A&M game:
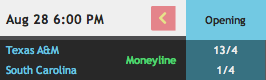
The probability that Texas A&M wins is 4 / 17 = 0.24, and the probability that South Carolina wins is 4 / 5 = 0.8 -- the same probabilities we got from the moneyline. Again, we should divide by the sum of the probabilities to get the true probabilities.
I use the KimonoLabs scraper to collect the data. Kimono can make scraping the web fast and painless, and it's the first thing I try if I have to webscrape.
I wrote the code in R, a free and widely-used statistics-oriented programming language. There are several excellent references for R beginners:
- Code School's free, interactive tutorial in R
- R in a Nutshell
- A number of freely available "quick reference" sheets such as ones by Tom Short, and staff at the University of Auckland
This software relies on R's shiny package. For more information on how to install this and other R packages, see here.
