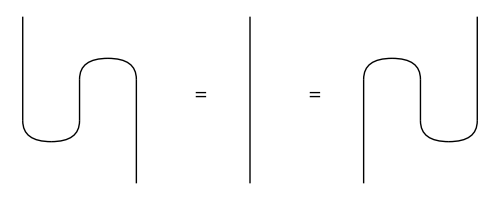DisCoPy is a tool box for computing with monoidal categories.
Diagrams are the core data structure of DisCoPy, they are generated by the following grammar:
diagram ::= Box(name, dom=type, cod=type)
| diagram @ diagram
| diagram >> diagram
| Id(type)
type ::= Ty(name) | type.l | type.r | type @ type | Ty()String diagrams (also known as tensor networks or Penrose notation) are a graphical calculus for computing with monoidal categories. For example, if we take ingredients as types and cooking steps as boxes then a diagram is a recipe:
from discopy import Ty, Box, Id
egg, white, yolk = Ty('egg'), Ty('white'), Ty('yolk')
crack = Box('crack', egg, white @ yolk)
merge = lambda x: Box('merge', x @ x, x)
swap = lambda x, y: Box('SWAP', x @ y, y @ x)
crack_two_eggs = crack @ crack\
>> Id(white) @ swap(yolk, white) @ Id(yolk)\
>> merge(white) @ merge(yolk)
crack_two_eggs.draw(path='docs/imgs/crack-eggs.png')Wires can be bended using two special kinds of boxes: cups and caps, which satisfy the snake equations, also called triangle identities.
from discopy import Cup, Cap
x = Ty('x')
left_snake = Id(x) @ Cap(x.r, x) >> Cup(x, x.r) @ Id(x)
right_snake = Cap(x, x.l) @ Id(x) >> Id(x) @ Cup(x.l, x)
assert left_snake.normal_form() == Id(x) == right_snake.normal_form()In particular, DisCoPy can draw the grammatical structure of natural language sentences encoded as reductions in a pregroup grammar (see Lambek, From Word To Sentence (2008) for an introduction).
from discopy import pregroup, Word
s, n = Ty('s'), Ty('n')
Alice, Bob = Word('Alice', n), Word('Bob', n)
loves = Word('loves', n.r @ s @ n.l)
sentence = Alice @ loves @ Bob >> Cup(n, n.r) @ Id(s) @ Cup(n.l, n)
pregroup.draw(sentence, path='docs/imgs/alice-loves-bob.png')Monoidal functors compute the meaning of a diagram, given an interpretation for each wire and for each box. In particular, tensor functors evaluate a diagram as a tensor network using numpy. Applied to pregroup diagrams, DisCoPy implements the distributional compositional (DisCo) models of Clark, Coecke, Sadrzadeh (2008).
import numpy as np
from discopy import TensorFunctor
F = TensorFunctor(
ob={s: 1, n: 2},
ar={Alice: [1, 0], loves: [[0, 1], [1, 0]], Bob: [0, 1]})
assert F(sentence) == np.array(1)Free functors (i.e. from diagrams to diagrams) can fill each box with a complex diagram,
while quivers allow to construct functors from arbitrary python functions.
The result can then be simplified using diagram.normalize() to remove the snakes.
from discopy import Functor, Quiver
def wiring(word):
if word.cod == n: # word is a noun
return word
if word.cod == n.r @ s @ n.l: # word is a transitive verb
return Cap(n.r, n) @ Cap(n, n.l)\
>> Id(n.r) @ Box(word.name, n @ n, s) @ Id(n.l)
W = Functor(ob={s: s, n: n}, ar=Quiver(wiring))
rewrite_steps = W(sentence).normalize()
sentence.to_gif(*rewrite_steps, path='autonomisation.gif', timestep=1000)pip install discopyThe tool paper is now available on arXiv:2005.02975, it was presented at ACT2020.
The documentation is hosted at readthedocs.io, you can also checkout the notebooks for a demo!