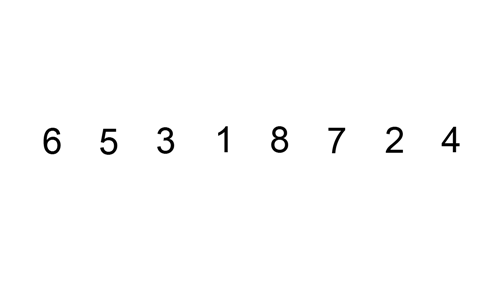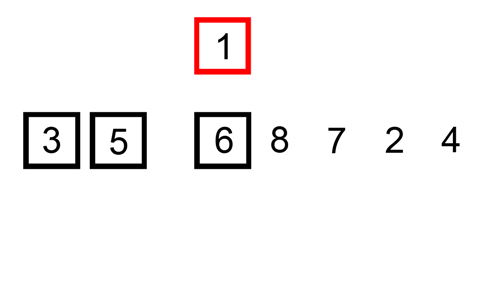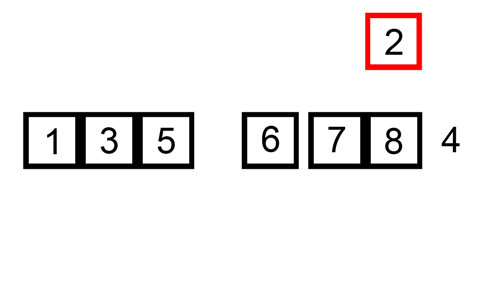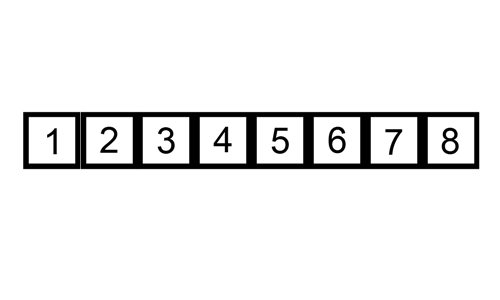InsertionSort

O InsertionSort é um algoritmo de ordenação que, dado uma estrutura (array, lista) constrói uma matriz final com um elemento de cada vez, uma inserção por vez. Assim como algoritmos de ordenação quadrática, é bastante eficiente para problemas com pequenas entradas, sendo o mais eficiente entre os algoritmos desta ordem de classificação.

Gif: Wikipedia

Veja exemplos abaixo que ilustram a implementação básica do algoritmo Insertion Sort em diferentes linguagens de programação. Vale ressaltar que existem diversas maneiras de implementar o algoritmo, com variações que podem torná-lo mais eficiente ou adaptá-lo para diferentes tipos de dados.

C

void insertionSort(int arr[], int n) {
    int i, key, j;
    for (i = 1; i < n; i++) {
        key = arr[i];
        j = i - 1;
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j = j - 1;
        }
        arr[j + 1] = key;
    }
}

Python

def insertionSort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i - 1
        while j >= 0 and arr[j] > key:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key

JavaScript

function insertionSort(arr) {
    for (let i = 1; i < arr.length; i++) {
        let key = arr[i];
        let j = i - 1;
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = key;
    }
}

Visualize a funcionalidade do codigo na pratica acessando o pages do projeto

Como funciona

Na implementação do algoritmo de InsertionSort, temos um loop que se repete sobre um array, começando a partir do segundo elemento (índice 1) e percorrendo todos os elementos até o final. Dentro deste loop, temos outro loop while que compara o elemento atual com o elemento anterior e, se o elemento atual for menor que o anterior, troca as suas posições. Este loop while continua até que o elemento atual esteja na posição correta.

Características

Apesar de ser menos eficiente do que algoritmos como Merge Sort e Quick Sort (de ordem O(nlog(n))), o Insertion Sort possui algumas características consideráveis:

• É de simples implementação, leitura e manutenção;
• In-place: Apenas requer uma quantidade constante de O(1) espaço de memória adicional;
• Estável: Não muda a ordem relativa de elementos com valores iguais;
• Útil para pequenas entradas;
• Muitas trocas, e menos comparações;
• Melhor caso: O(n), quando a matriz está ordenado;
• Médio caso: O(n²/4), quando a matriz tem valores aleatórios sem ordem de classificação (crescente ou decrescente);
• Pior caso: O(n²), quando a matriz está em ordem inversa, daquela que deseja ordenar.

Vantagens e Desvantagens

• Vantagem:

  • É o método a ser utilizado quando o arquivo está "quase" ordenado;
  • É um bom método quando se desejar adicionar poucos elementos em um arquivo já ordenado, pois seu custo é linear;
  • O algoritmo de ordenação por inserção é estável.

• Desvantagem:

  • Alto custo de movimentação de elementos no vetor.