The Josephus Problem:

Table of Contents:

• What is the Josephus Problem?
• Variations of the Josephus Problem
• About the Implementation
• Features of the CircularList class
• Author
• Contributing
• Show your support

What is the Josephus Problem?

The Josephus Problem is a theoretical problem related to a certain counting-out game. The counting out begins at some point in the circle and proceeds around the circle in a fixed direction. In each step, a certain number of people are skipped and the next person is left out of the game. The elimination proceeds around the circle (which is becoming smaller and smaller as the executed people are removed), until only the last person remains, who is declared to be the winner.

An excellent video on the Josephus Problem was published on the YouTube platform by Numberphile and a parametric animation on the topic can be viewed thanks to Desmos.

Variations of the Josephus Problem:

The original Josephus Problem consisted of a Jewish historian Flavius Josephus and his 40 soldiers who were trapped in a cave by Roman soldiers. The Jews chose suicide over capture, and thus arranged themselves in a circle under the edict that every other man would be executed by the fellow soldier to his right iteratively until only one remains. The last survivor would have to kill himself. The main character of the story - Josephus - who opposed to the corporate suicide wanted to figure out where to position himself in a circle so as to save himself from death and surrender to the Romans.

Another popular version of the Josephus Problem involves 15 Turks and 15 Christians aboard a ship in a storm which will sink unless half the passengers are thrown overboard. All 30 stand in a circle and every ninth person is to be tossed into the sea. The Christians need to determine where to stand to ensure that only the Turks are tossed.

The generalisation of the problem consists of N people standing in a circle where every k-th man will be executed going around the circle until M men remain. The solution to the problem is a list of positions of the men who would avoid being executed.

About the Implementation

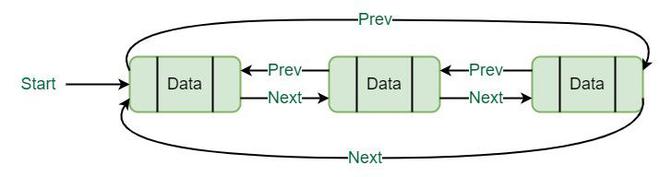
To solve the Josephus Problem in an ambitious and educative way a self-implemented circular doubly linked list was used. The CircularList class was implemented as a class template with one template parameter. It can be used in other projects as it is independent from the Josephus Problem context. The data structure used in the project is best explained visually using the picture below:

The incentive for such an implementation was also the fact that STL doesn't support cycling data structures.

The JosephusProblemSolver is a class template which makes use of the public interface of the CircularList. It provides two different overloaded versions of operator():

Overloaded operator:	Explanation:
CircularList<T> operator()(size_t numberOfSoldiers = 41, size_t numberOfSurvivors = 1, size_t executionStep = 2) const	Returns a CircularList of positions (positions start at 1) which are the solution of the Josephus Problem. Its parameters allow the user to solve the problem in a most generic form.
CircularList<T> operator()(std::string filename, size_t numberOfSurvivors = 1, size_t executionStep = 2) const	Does the same as above, except the numberOfSoldiers is predetermined by the contents of the file filename. It creates solution_filename with solution to the Josephus Problem. In case the filename doesn't exist or other file-related errors, throws FileException (self-implemented exception class which inherits from std::exception).

The format of the input files and output files is described in: numbers.txt, soldiers.txt, solution_numbers.txt and solution_soldiers.txt.

An exemplary usage of all implemented classes can be found in main.cpp cource file.

Features of the CircularList class:

The CircularList class was written in such a way, so as to imitate an STL container. All the public interface of the CircularList class with a short explanation is correlated in the tables below:

Member function:	Explanation:
Constructors:
CircularList()	Default constructor (empty list).
CircularList(size_t n, const value_type& val)	Creates a list with n elements of the value val.
CircularList(const CircularList<T>& other)	Copy constructor.
CircularList(CircularList<T>&& other)	Move constructor.
template <class InputIterator> CircularList(InputIterator first, InputIterator last)	An STL-like constructor (iterators can be used).
Destructor:
~CircularList()	Destructor.
Assignment operators:
CircularList<T>& operator=(const CircularList<T>& other)	Copy assignment operator.
CircularList<T>& operator=(CircularList<T>&& other)	Move assignment operator.
Element access:
reference front()	Returns the first element. If the list is empty, the behaviour is undefined.
const_reference front() const	The same as above.
reference back()	Returns the last element. If the list is empty, the behaviour is undefined.
const_reference back() const	The same as above.
Capacity:
bool empty() const	Resturns true if the list is empty.
size_t size() const	Resturns the number of elements of the list.
Modifiers:
void clear()	Empties the list removing its elements.
void push_back(const value_type& val)	Adds val to the back of the list.
void pop_back()	Removes the last element. If the list is empty, it does nothing.
void push_front(const value_type& val)	Adds val to the front of the list.
void pop_front()	Removes the first element. If the list is empty, it does nothing.
void insertAfter(size_t position, size_t howMany, const value_type& val)	Inserts elements of value val howMany times after the given position (indexing starts with 0).
template <class InputIterator> void insertAfter(size_t position, InputIterator first, InputIterator last)	The same as above (STL-like method).
void insertSorted(const value_type& val)	Inserts val at the first position which is less then val.
void remove(const value_type& val)	Removes all occurences of val.
void remove_if(std::function<bool(const value_type& val)> pred)	Removes all elements based on the predicate pred.
void removeEveryNUntilMRemains(size_t n, size_t m)	Self-explanatory.
void reverse()	Reverses the list.
void generateN(size_t n, std::function<value_type(void)> generator)	Pushes back n elements of the value generated by the generator to the list.
void bubbleSort()	Sorts the list in ascending order.
bool pushFromFile(std::string filename)	Pushes back elements saved in a text file filename. If the format of the file is incorrect or the file doesn't exist, it does nothing.
std::ostream& print(std::ostream& os, std::string delimeter = " ") const	Prints all elements of the list to the output stream os.
Overloaded operators:
friend bool operator== <> (const CircularList<T>& lhs, const CircularList<T>& rhs)	Returns true if lhs and rhs have the same elements (elements are compared using operator==).
friend bool operator!= <> (const CircularList<T>& lhs, const CircularList<T>& rhs)	!(lhs == rhs)
friend CircularList<T> operator+ <> (const CircularList<T>& lhs, const CircularList<T>& rhs)	Returns a new list containing all elements of lhs and rhs preserving the initial order of elements.
CircularList<T> operator+=(const CircularList<T>& other)	Pushes back a copy of all elements from other to *this.
friend std::ostream& operator<<(std::ostream& os, const CircularList<T>& cl)	Overloaded operator<<.

Member types:	Explanation:
value_type	T
reference	T&
const_reference	const T&
pointer	T*
const_pointer	const T*

Author:

My GitHub: @adamgracikowski

Contributing:

All contributions, issues, and feature requests are welcome! 🤝

Show your support:

Give a ⭐️ if you like this project and its documentation!