graffiti - a library for declarative computation

Installation

pip install graffiti

or

1. git clone https://github.com/SegFaultAX/graffiti
2. cd graffiti/
3. To install: python setup.py install
4. To get development dependencies: pip install -r requirements.txt
5. To run tests: nosetests
6. To audit source: python setup.py audit

Check out my blog post for more background on the "why" of this project. Get in touch if you have any comments or questions!

Inspired by Prismatic's Graph library (https://github.com/prismatic/plumbing)

Overview

from graffiti import Graph

stats_descriptor = {
    "n": lambda xs: len(xs),
    "m": lambda xs, n: sum(xs) / n,
    "m2": lambda xs, n: sum(x ** 2 for x in xs) / n,
    "v": lambda m, m2: m2 - m ** 2
}

graph = Graph(stats_descriptor)
graph({ "xs": [1, 2, 3, 4, 5] })
#=> {'xs': [1, 2, 3, 4, 5], 'n': 5, 'm': 3, 'm2': 11, 'v': 2}

# if pydot is installed
graph.visualize()

Tutorial

Consider the following perfectly reasonable Python code:

def stats(xs):
    n = len(xs)
    m = sum(xs) / n
    m2 = sum(x ** 2 for x in xs) / n
    v = m2 - m ** 2

    return {
        "xs": xs,
        "n": n,
        "m": m,
        "m2": m2,
        "v": v,
    }

The first computation is based on our input (xs), and each additional computation builds up more values based on things we've computed already. It's convenient to visualize this computation as a graph with the user inputs at the root and values we're interested in at the leaves.

graffiti allows you to structure your computation in exactly that fashion:

stats_graph = {
    "n": lambda xs: len(xs),
    "m": lambda xs, n: sum(xs) / n,
    "m2": lambda xs, n: sum(x ** 2 for x in xs) / n,
    "v": lambda m, m2: m2 - m ** 2
}
graph = Graph(stats_graph)
graph({ "xs": range(100) })

graffiti finds the relationships between the nodes in your graph and determines the optimal execution order. Leaves in the graph are computed lazily which means we can choose to only evaluate the ones we're interested in:

graph({ "xs": range(100) }, _keys={"m", "n"})

In this case, graffiti will only evaluate what's needed to compute m and n, but not the rest of the graph. You can also build nested graphs with dependencies across nesting levels:

stats_graph = {
    "n": lambda xs: len(xs),
    "m": lambda xs, n: sum(xs) / n,
    "m2": lambda xs, n: sum(x ** 2 for x in xs) / n,
    "v": lambda m, m2: m2 - m ** 2,
    "order": {
        "sorted": lambda xs: sorted(xs),
        "reversed": lambda xs: sorted(xs, reverse=True)
    },
}

graph = Graph(stats_graph)
graph({ "xs": range(100) })
graph({ "xs": range(10) }, _keys={"order"})

Again, none of the unecessary nodes will be computed. Nodes in the graph can also contain optional arguments:

graph = Graph({ "mul": lambda n, p=10: n * p })
graph({ "n": 10 }) # mul == 100
graph({ "n": 10, "p": 20 }) # mul == 200

If the optional key is provided as an input to the graph evaluator, it will override the default value of the node. This makes it easy to play with different values or settings as the computation flows through your pipeline.

Finally, graphs are resumable. Since a graph object takes a dict as input and returns a dict as output, you can replay a previously generated dict as the input to the next thereby reusing all previously computed values:

stats_graph = {
    "n": lambda xs: len(xs),
    "m": lambda xs, n: sum(xs) / n,
    "m2": lambda xs, n: sum(x ** 2 for x in xs) / n,
    "v": lambda m, m2: m2 - m ** 2,
}

graph = Graph(stats_graph)
v1 = graph({ "xs": [1,2,3] }, _keys={"n"}) # just n
v2 = graph(v1, _keys={"m"}) # v1 + just m
v3 = graph(v2) # the rest of the graph

This allows you to defer the evaluation of expensive keys until the moment they're actually needed without duplicating previous computations.

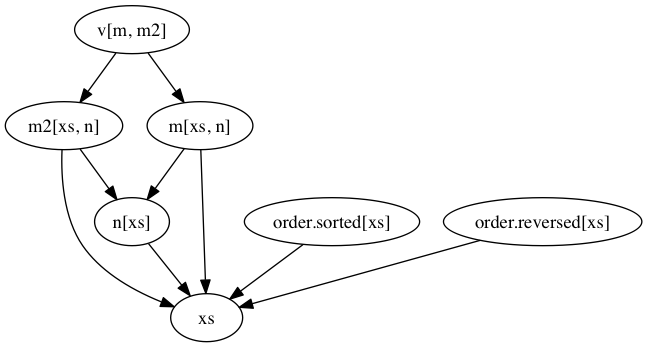
graffiti also supports drawing the transitive graph of dependencies:

stats_graph = {
    "n": lambda xs: len(xs),
    "m": lambda xs, n: sum(xs) / n,
    "m2": lambda xs, n: sum(x ** 2 for x in xs) / n,
    "v": lambda m, m2: m2 - m ** 2,
    "order": {
        "sorted": lambda xs: sorted(xs),
        "reversed": lambda xs: sorted(xs, reverse=True)
    },
}
graph = Graph(stats_graph)
graph.visualize()

Using graffiti allows you to structure your computation and the complex interdependencies therein naturally and efficiently. Most importantly, your computational pipeline is just data. That means it's easy to inspect, easy to reason about, and easy to build tooling around.

This project is still under active development. Contact me on Twitter @SegFaultAX if you have any questions, comments, or bug reports.

License

Copyright 2014 Michael-Keith Bernard

Availabe under the MIT License. See LICENSE for full details.