Data Structures and Algorithm

Table of Contents

• Key Takeaways
  • Dynamic Programming Takeaways
  • Memoization Recipe
  • Tabulation Recipe
  • Understanding time and space complexities of FIBONACI RECURSIVE Problem
  • Tips and Tricks
• Big O Notation
• Problem Solving Patterns
  • Frequency Counter Pattern
  • Multiple Pointers Pattern
  • Sliding Window Pattern
  • Divide and Conquer Pattern
  • Tortoise and Hare Pattern
• Recursion
• Searching Algorithms (Linear, Binary, Naive)
• Sorting
  • Bubble Sort
  • Selection Sort
  • Insertion Sort
  • Merge Sort
  • Quick Sort
  • Heap Sort
  • Radix Sort
  • Count Sort
  • Comparison of Sorting Algorithms
• Data Structures
  • Classes and Instances
  • Singly Linked Lists
  • Doubly Linked Lists
  • Stack and Queues
  • Binary Search Tree
  • Tree Traversal
    • Breadth First Search (BFS)
    • Depth First Search (DFS)
  • Binary Heaps
  • Priority Queue
  • Hash Table/Hash Map
    • Dealing with collisions
  • Graphs
    • Graph Traversal
    • Dijkstras Algorithm (Shortest Path algorithm)
• Optimization problem
• Dynamic Programming
• Backtracking
• Greedy Algorithm
• DP vs Greedy algorithm vs Backtracking

Key Takeaways

• Accept n no of arguments in javascript - use arguments keyword or spread operator

function multipleArguments(...arr) {
  return arr.sort();
}

• To avoid encountering duplicates again, splice them off
• To remove duplicates, make a set
• BFS is implemented using Queue,
  DFS is implemented using Stack or Recursion (which internally uses Call Stack)
• Whenever a function has to return either True/False, initially set result to True, if at any point condition fails set it to False, break, and return result.
• Whenever a Problem has a sorted structure, Try using Multiple Pointers Pattern with while loop before Frequency Counter Pattern
• Whenever we have an array or string and we are looking for a continuous subset of data, use Sliding Window Pattern
• For Dynamic programming - Visualise the problem as a tree (nodes represnent arguments, the problem should shrink to smaller sub problems eventually base cases)
• Two methods to solve problems with Dynamic Programming
  Memoization - Storing the results in memo and passing it to every call
  Tabulation - Storing the result of a previous result in a table (usually an array), Usually done using iteration
• sum = (n*(n-1))/2 Guass formula to compute the sum of the first n natural numbers in constant time
• When numbers from 1 to n are mentioned in an array use sum = (n*(n-1))/2
• XOR operator can be used in many problems
  • If we take XOR of zero and some bit, it will return that bit a ^ 0 = a
  • If we take XOR of two same bits, it will return 0 a ^ a = 0
  • XOR all bits together to find the unique number a ^ b ^ c ^ a ^ c = b
• Logarithm is the inverse of exponentiation
  log₂(8) = 3 --------> 2³ = 8
• Binary Logarithm of a number roughly measures the no of times you can divide the no by 2 before you get a value less then or equal to 1
• To track already visited nodes, Instead of maintaining a visited hash, directly mark entries as 1 or 'v' in the array or matrix itself
  Eg - 200_no_of_islands problem, we mark visited lands by setting them as 'v' so we dont count them again
• When we want to keep a record of which all nodes to check recursievely, prefer using stack instead of queue
  stack - push pop, queue - push shift, pop is constant time, shift is linear time
• While storing variables, Instead of using an array [2,5,7] and then checking arr.includes(5)
  use [0,0,1,0,0,1,0,1] and then check arr[5] == 1
  Eg - Set matrix zero , this increases space complexity but reduces time complexity as arr.includes is O(n) arr[5] is O(1)
• When you want fast access (like hash) and want sequential order (like array)
  use count array, eg [2,5,7] to [0, 0, 1, 0, 0, 1, 0, 1], eg - last stone weight
• If we need the max/min values after every iteration and for that if we need to sort an array in a loop, it can be simplified using a priority queue or heap
  Eg - last stone weight
• Use greedy algorithm for problems of the kinds where we first fill the jar with stones, then pebbles, and then sand
  Eg: Maximum units on a truck, Maximum icecream bars
• If in a problem we need to calculate all possible permutations and combinations, it can be done using backtracking Eg: Binary Watch
• If in a problem we need to calculate all possible permutations and combinations, it can be done using backtracking
• If in a problem we need all solutions and not the best or worst (max or min) use backtracking. Eg - Binary watch
• To detect cycle in a linked list, use hare tortoise pattern, two pointers, j at twice the speed of i
  Eg: Linked list cycle
• While merging two sorted arrays, do not forget to add leftover individual elements too
  Eg: Merge sort
  Median of Two Sorted Arrays
• For some sliding window problems, where you need to move the window and remove and add elements from either side, consider using a double-ended-queue Eg: Sliding window max
• To cyclically loop through an array, use the modulo operator index = (index + 1) % array.length
• To loop over a directions array directions = ["up", "right", "down", "left"] cyclically, d = (d+1) % 4
  Here d will take values up, right, down, left, up, right, ...
  Eg Spiral matrix

Dynamic Programming Takeaways

• Refer - https://www.youtube.com/watch?v=oBt53YbR9Kk&t=4321s

• If the Brute force solution ---> O(2 ^ n), it is probably a DP question

• For Dynamic programming - Visualise the problem as a tree (nodes represnent arguments, the problem should shrink to smaller sub problems eventually base cases)

• Two methods to solve problems with Dynamic Programming
  Memoization - Storing the results in memo and passing it to every call
  Tabulation - Storing the result of a previous result in a table (usually an array), Usually done using iteration

• For a problem whose solution will be Recursive, Visualize it like a tree

  If there is a choice between two options,
  eg Right/Down in grid_traversal_memoization_dp, Add/Subtract in dp_target_sum.js
  Represent them as left and right child of tree

• To represent a problem of checkSum into tree - checkSum(7, [5, 4, 3, 7]) -> true checkSum(7, [2, 4]) -> false

  

---

Memoization Recipe

1. Make It Work

• Visualise as a tree (nodes represnent arguments, the problem should shrink to smaller sub problems eventually base cases)
• Implement tree using recursion
• Test it

1. Make Efficient

• Add a memo object (keys representing arguments and value represnting return values for those arguments)
• Pass memo object with all recursive calls
• Add base case to check memo object
• Store calculate return values in the memo

---

Tabulation Recipe

---

Understanding time and space complexities

• Understanding time and space complexities of FIBONACI RECURSIVE Problem

  const foo(n) => {
    if(n <= 1) return;
    foo(n-1);
  }
  
  
  // Time complexity - O(n)
  // Space complexity - O(n)

  const bar(n) => {
    if(n <= 1) return;
    bar(n-2);
  }
  
  
  // Time complexity - O(n)
  // Space complexity - O(n)

  const dib(n) => {
    if(n <= 1) return;
    dib(n-1);
    dib(n-1);
  }
  
  
  // Time complexity - O(2 ^ n)
  // Space complexity - O(n)

  

  Space Complexity is O(n), Once a base case is reached the stack frame is popped out of the stack ,and once the left child is removed after that the right child is added Hence at any point there are only n calls in call stack, which is clear in the visual
  

---

Big O Notation

• Used to compare and rate different working implementations
• Allows us to talk formally about how runtime of algo grows as input grows
• considers upper bound, worst case senario
• doesnt care about precision just general trend

1. Time Complexity

   Problem - Add numbers from 0 upto n including n
   
   Approch 1 - initialize total=0, using a loop and adding each no
   Time Taken ~ 1.5 sec
   As n grows, no of operations grow roughly in proportion to n ---> O(n)
   
   Approch 2 - sum till n = n * (n-1) / 2
   Time Taken ~ 0.001 sec
   3 simple operations regardless to the size of n ---> O(1)
   

   Common Time complexities

   • no loops -> O(1)
   • one loop -> O(n)
   • two loops -> O(2n) -> O(n)
   • two nested loops -> O(n²)

   Comparison of common time complexities
   

   On a grand scale
   

   // Determine the time complexity for the following function
   
   function logAtMost10(n) {
     for (var i = 1; i <= Math.min(n, 10); i++) {
       console.log(i);
     }
   }
   
   // O(1) - no mater what n is it runs 10 times

2. Space Complexity

   Space required by the algorithm, not including space taken by the inputs

   Rules of thumb to calculate space complexity

   • Most primitives (nos, chars, booleans, undefined, null) are constant space
   • String require n (length of string) space
   • Arrays, objects require n (length of arrays, keys of object)space

   // Determine the space complexity for the following function
   
   function onlyElementsAtEvenIndex(array) {
     var newArray = Array(Math.ceil(array.length / 2));
     for (var i = 0; i < array.length; i++) {
       if (i % 2 === 0) {
         newArray[i / 2] = array[i];
       }
     }
     return newArray;
   }
   
   // O(n) - if n is 10 space req is 5, n=100 50, n=200 100 ... increases linerly with n

3. Logarithms

   Logarithm is the inverse of exponentiation

   log₂(8) = 3 --------> 2³ = 8

   Binary Logarithm of a number roughly measures the no of times you can divide the no by 2 before you get a value less then or equal to 1

   log(4 billion something) ---> 32
   log(8 billion something) ---> 33
   log(16 billion something) ---> 34

   When input doubles, time to execute increases by just one operation

   Time to execute an Algorithm with O(n) complexity, 4 billion input size ~ 4 Billion nanoseconds ~ 4 days
   Time to execute an Algorithm with O(log n) complexity, 4 billion input size ~ 32 nanoseconds ~ almost instant

4. 2ⁿ Time Complexity

For a problem like following, Each node represnts one operation to be done
Since the root (level 1) will have one node, and each following level will have 2*node of parent
total time taken = 1 * 2 _ 2 _ 2 ....(n times)
which is 2ⁿ
The space complexity for this problem is O(n) as we reach base case it returns a value
Whenever a new node is added to the stack, an older value return n goes out, hence space complexity stays O(n)

---

Analyzing Performance of Arrays and Objects

• Objects

  • unordered, key value pairs
  • Values are reffered by keys, firstName, color, etc
  • Use objects when you dont need order
  • when you need fast access, insertion and removal
  • BigO of objects - Access O(1), Insertion O(1), Removal O(1), Searching O(n)
  • BigO of predefined methods - Object.keys O(n), Object.values O(n), Object.entries O(n), Object.hasOwnProperty O(1)

• Arrays

  • Arrays are ordered

  • Values are reffered by indexes, 0th item, 1st item...

  • Use arrays when you need order

  • BigO of Arrays - Access O(1), Searching O(n)

  • Insertion/Removal at end O(1), insertion/removal at begining O(n) as we have to shift all existing values

  • shift() and unshift() is much costlier then push() and pop()

  • BigO of array methods

    • push() pop() - O(1)
    • shift() unshift() - O(n)
    • concat() - O(n+m) -> O(n)
    • slice() splice() - O(n) as rest part needs to be reordered
    • sort() - O(n log n) VERY EXPENSIVE
    • forEach, map, filter, reduce - O(n) process each element once

---

Problem Solving Patterns

1. Frequency Counter Pattern

   The Idea behind frequency counter is use an object to construct a profile of an array or a string

   Example
   Write a function 'same' which accepts two arrays,
   The function should return true if every value in the array has its corresponding value squared in second array,
   The frequency of values must be same
   same([1, 2, 3], [4, 1, 9]) // true
   same([3, 4, 2], [4, 16]) // false
   same([1, 2, 1], [4, 4, 1]) // false

   function same(arr1 = [], arr2 = []) {
     let result = true;
     arr1.forEach((value) => {
       const index = arr2.indexOf(value * value);
       if (index < 0) {
         result = false;
         return result;
       }
       arr2.splice(index, 1);
     });
     return result;
   }
   
   // forEach O(n), indexOf O(n), splice O(n) ---> O(n*n)

   // frequency counter refactored
   function same(arr1 = [], arr2 = []) {
     const freq1 = {};
     const freq2 = {};
     arr1.forEach((val) => (freq1[val] ? (freq1[val] += 1) : (freq1[val] = 1)));
     arr2.forEach((val) => (freq2[val] ? (freq2[val] += 1) : (freq2[val] = 1)));
     for (let key in freq1) {
       if (!freq2[key * key]) {
         return false;
       }
       if (freq1[key] !== freq2[key * key]) {
         return false;
       }
     }
     return true;
   }
   
   // forEach O(n), for O(n) ---> O(3n) ----> O(n)

   
   Example 2 -
   Given two strings, determine if second string is the anagram of first
   An anagram is a word formed by rearranging letters of another such as cinema from iceman
   validAnagram('', '') // true
   validAnagram('cinema', 'iceman') // true
   validAnagram('anagram', 'nagaram') // true
   validAnagram('aaz', 'zza') // false
   validAnagram('rat', 'car') // false
   validAnagram('awesome', 'awesom') // false

   function validAnagram(str1 = "", str2 = "") {
     if (str1.length !== str2.length) return false;
     const hash = {};
     for (var i in str1) {
       hash[str1[i]] ? (hash[str1[i]] += 1) : (hash[str1[i]] = 1);
     }
     for (var i in str2) {
       if (!hash[str2[i]]) {
         return false;
       }
       hash[str2[i]] -= 1;
     }
     return true;
   }

   Leetcode problems

   • Same
   • Anagram

2. Multiple Pointers Pattern

   Create pointers that correspond to an index or position, and move toward the beginning end or middle based on condition. mostly used on sorted linear structures

   Example 1 - One pointer from left and one from right
   Write a function 'sumZero' which accepts sorted array of integers,
   The function should return first pair where sum is 0,
   Return an array that includes both nos that sum upto 0 or undefined if pair doesnt exist
   sumZero([-3, -2, -1, 0, 1, 2, 3]) // [-3, 3]
   sumZero([-2, 0, 1, 3]) // undefined
   sumZero([-4, -3, -2, -1, 0, 1, 2, 5]) // [-2, 2]
   sumZero([-4, -3, -2, -1, 0, 1, 2, 3, 10]) // [-3, 3]

   // brute force
   function sumZero(arr = []) {
     for (let i = 0; i < arr.length; i++) {
       for (let j = i + 1; j < arr.length; j++) {
         if (arr[i] + arr[j] === 0) {
           return [arr[i], arr[j]];
         }
       }
     }
   }
   
   // nested loop ---> O(n*n)

   // multiple pointers one from left and one from right
   function sumZero(arr = []) {
     let left = 0;
     let right = arr.length - 1;
     while (left < right) {
       const sum = arr[left] + arr[right];
       if (sum === 0) {
         return [arr[left], arr[right]];
       }
       sum > 0 ? right-- : left++;
     }
   }
   
   // while loop ---> O(n)

   
   Example 2 -
   Write a function 'countUniqueValues' which accepts sorted array of integers, and counts unique values in the array
   countUniqueValues([1, 1, 1, 1, 1, 3]) // 2
   countUniqueValues([1, 2, 3, 4, 4, 4, 7, 7, 12, 12, 13]) // 7
   countUniqueValues([]) // 0
   countUniqueValues([-2, -1, -1, 0, 1]) // 4

   // brute force - use set or maybe hash n increase count when new value put into hash
   function countUniqueValues(arr = []) {
     const set = new Set(arr);
     return set.size;
   }

   // multiple pointers refactored ---> O(n)
   function countUniqueValues(arr = []) {
     let count = 0;
     let ptr1 = 0;
     let ptr2 = 1;
     while (ptr2 <= arr.length) {
       if (arr[ptr1] === arr[ptr2]) {
         ptr2++;
       } else {
         count++;
         ptr1 = ptr2;
         ptr2++;
       }
     }
     return count;
   }

   Leetcode problems

   • Count unique values
   • Sum zero

3. Sliding Window Pattern

   The Sliding Window Pattern is commonly used in problems that require finding subarrays or sublists that satisfy certain conditions.

   The basic idea behind the Sliding Window Pattern is to maintain a "window" or a subrange of elements within the given array or sequence and slide it through the array in a systematic way. As you move the window, you update its state to reflect the current portion of the array you are considering.

   Example
   write a function maxSubarraySum which accepts an array of integers and a number called n.
   The function should calculate the maximum sum of n consecutive elements in an array.
   maxSubarraySum([1,2,5,2,8,1,5], 2) // 10
   maxSubarraySum([1,2,5,2,8,1,5], 4) // 17
   maxSubarraySum([4,2,1,6], 1) // 6
   maxSubarraySum([4,2,1,6,2], 4) // 13

   // brute force --> O(n*m)
   function maxSubarraySum(arr = [], num) {
     if (num > arr.length) {
       return null;
     }
     let max = -Infinity;
     for (var i = 0; i <= arr.length - num; i++) {
       let temp = 0;
       for (j = i; j < i + num; j++) {
         temp += arr[j];
       }
       max = temp > max ? temp : max;
     }
     return max;
   }

   // sliding window --> O(m + n)
   function maxSubarraySum(arr = [], num) {
     if (num > arr.length) {
       return null;
     }
     let max = 0;
     let tempSum = 0;
     for (var i = 0; i < num; i++) {
       tempSum += arr[i];
     }
     max = tempSum > max ? tempSum : max;
     for (var j = num; j < arr.length; j++) {
       tempSum = tempSum + arr[j] - arr[j - num];
       max = tempSum > max ? tempSum : max;
     }
     return max;
   }
   
   /* In this case - The size of window is n elements, when we move the window forward, we add the current element and subtract the earliest element 
   
   Eg - maxSubarraySum([1,2,5,2,8,1,5], 4)
   tempSum = 1+2+5+2 = 10
   
   In the loop, 10+8-1 = 17, 17+1-2=16, 16+5-5=16
   [0,0,0,10,17,16,16] // max is 17 
   */

   Leetcode problems

   Colorful rope

4. Divide and Conquer Pattern

   This pattern involves dividing a dataset into smaller chunks and then repeating a process with a subset of data

   • Quick sort and Merge sort are examples of divide and conquer
   • Binary serch is also an example of divide and conquer

   Example
   Given a sorted array and a value, write a function search which returns index of value in that array
   return -1 if value not found
   search([1, 4, 6, 9, 44, 60], 9) // 3

   // Linear Search - O(n)
   function search(arr, val) {
     for (let i = 0; i < arr.length; i++) {
       if (arr[i] === val) {
         return i;
       }
     }
     return -1;
   }

   // Binary Search - O(log n)
   

5. Tortoise and Hare Pattern

   The "tortoise and hare" pattern, also known as Floyd's cycle-finding algorithm, is a technique used in data structures and algorithms (DSA) to detect cycles in a sequence, such as a linked list.

   The concept is to have two pointers, one moving at a slower pace (tortoise) and another moving at a faster pace (hare)

   If there is a cycle in the structure, the fast pointer will eventually catch up to the slow pointer, and they will meet at some point within the cycle.

   Leetcode problems

   Linked list cycle

---

Tips and Tricks

// Traverse deeply nested object using recursion

function nestedLoop(obj) {
  const res = {};
  function recurse(obj, current) {
    for (const key in obj) {
      let value = obj[key];
      if (value != undefined) {
        if (value && typeof value === "object") {
          recurse(value, key);
        } else {
          // Do your stuff here to var value
          res[key] = value;
        }
      }
    }
  }
  recurse(obj);
  return res;
}

// Traverse deeply nested object and append keys

function getArray(obj) {
  const result = [];
  function traverseObject(obj, current, appendedKeys = "") {
    for (const key in obj) {
      let value = obj[key];
      if (value != undefined) {
        if (value && typeof value === "object") {
          if (key === "amount") {
            const data = {};
            data[appendedKeys] = value.value;
            result.push(data);
          } else {
            traverseObject(value, key, appendedKeys.concat(key));
          }
        }
      }
    }
  }
  traverseObject(obj);
  return result;
}

// Accept n no of arguments in javascript - use arguments keyword or spread operator

function multipleArguments(...arr) {
  return arr.sort();
}

---

Recursion

A function that calls itself, until it reaches a base case

Recursion is used by

• JSON parse / JSON stringify
• document.getElementById and DOM traversal algorithms
• tree / graph traversals

The call stack

• A built in data structure that manages what happens when functions are invoked
• uses the stack data structure
• when a function is invoked it is pushed on top of stack, when return is seen or function ends it is poped
• observe the call stack in dev tools by adding breakpoints to the snippet

Example 1 - Factorial

  5! = 5 * 4 * 3 * 2 * 1
  n! = n * n-1 * n-2 * .... * 2 * 1
  n! = n * n-1!

// Iterative way
function factorial(num) {
  let total = 1;
  for (var i = num; i > 1; i--) {
    total = total * i;
  }
  return total;
}

// Recursion
function factorial(num) {
  if (num === 1) return 1;
  return num * factorial(num - 1);
}

Example 2 - Fibonacci
using recursion write a function that returns nth no in fibonacci series. Fibonacci seq - 1, 1, 2, 3, 5, 8, 13
fib(4) // 3
fib(5) // 5
fib(10) // 55

function fib(n) {
  if (n <= 2) return 1;
  return fib(n - 1) + fib(n - 2);
}

Note - Fibonacci function can be further optimized using dynamic programming

Helper Method Recursion

• A design pattern to use recursion for arrays and strings
• We have an outer function and inside the outer function we have an recursive helper function which calls itself
• The reason we do this is say we deifine result = [ ], whenever the recursive function calls itself the Result will reset

Example - Find all odds in a array using Helper Method Recursion

function collectOddValues(arr) {
  let result = [];
  function helper(input) {
    if (input.length === 0) return; // base condition
    if (input[0] % 2 !== 0) result.push(input[0]);
    helper(input.slice(1));
  }

  helper(arr);
  return result;
}

---

Searching Algorithms (Linear, Binary, Naive)

1. Linear Search

   • Checking each item one at a time
   • Time complexity is O(n)

2. Binary Search

   • Divide the structure into two halves using a pivot point (middle value), search on the left or right
   • Repeatedly dividing the search interval in half
   • Only works on sorted structures
   • Time complexity is O(log n)

   Binary search Implementation

3. Search for substring in a string

   Example - search for omg in wowomgzomg
   Brute force - loop over the longer string,nested loop over shorter string, if characters dont match break out of inner loop, if you complete inner loop increment count --> O(n _ m) -> O(n _ n)

---

Sorting

Sorting is the process of rearranging items in collection, so that items are in some kind of order
[View sorting algorithm animation]: https://www.toptal.com/developers/sorting-algorithms
[View Individual algo step by step]: https://visualgo.net/en/sorting

• Javascript default sort [6, 4, 15, 10].sort() returns [10, 15, 4, 6]
• Javascript default sort is according to string Unicode code points
• We can pass in a comparator function to tell javascript how to sort

---

Bubble Sort

An Algorithm where the largest value bubble up to the top, one at a time

• In one pass, compare two values, if larger no is before smaller then swap,else continue
• After one pass the largest value reaches the top, ie the end of array
• Repeat for i-1
• optimization for an nearly sorted array, count if any swaps were made in last pass, if no swaps were made the array is already sorted
• BigO of bubble sort O(n * n)
• BigO for nearly sorted data O(n)

---

Selection Sort

Simillar to bubble sort,but places small values into sorted position

• In one pass, find the smallest value in the array and place it/swap it with the first (i th) value
• After one pass the smallest value reaches the start of the array
• Repeat from i + 1
• No of swaps made is much lower the bubble sort
• Works poorly for nearly sorted data as compared to bubble sort, as still have to loop the entire array to find the min value
• BigO of selection sort O(n * n)

---

Insertion Sort

Instead of finding largest or smallest, it takes one element at a time and places it where it should go in the sorted portion

• Works for continuously changing data, if new values are added to the end of the array. This is because insertion sort is adaptive, meaning it becomes more efficient when dealing with partially sorted data.

• It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. However, insertion sort is often used for its simplicity and efficiency on small data sets or partially sorted data.

• BigO of insertion sort O(n * n)

  How insertion sort works:

  1. Start from the second element (index 1) of the array.
  2. Compare the current element with its predecessor.
  3. If the current element is smaller than its predecessor, compare it with the elements before. Move the greater elements one position up to make space for the current element. Repeat this process until you find an element smaller than the current one or reach the beginning of the array.
  4. Place the current element in the correct position in the sorted part of the array.
  5. Repeat steps 2-4 for each element in the array until the entire array is sorted.

  function insertionSort(arr) {
    const n = arr.length;
  
    for (let i = 1; i < n; i++) {
      let currentElement = arr[i];
      let j = i - 1;
  
      while (j >= 0 && currentElement < arr[j]) {
        arr[j + 1] = arr[j];
        j--;
      }
  
      arr[j + 1] = currentElement;
    }
  }

---

Merge Sort

Split, sort, merge

• Bubble sort, Selection sort, Insertion sort dont scale well for longer arrays
• Bubble sort roughly takes 20 sec for 10000 elements while merge sort takes 1 sec
• Time complexity of Merge sort O(n log n) and space complexity is O(n)
• Merge sort uses the fact that an array with 0 or 1 element is already sorted
• Works by decomposing the array into smaller arrays of 0 or 1 elements, then building up a newly sorted array
• How BigO of merge sort is O(n log n) ?
  As no of elements(n) grows the no of times we split grows by log n.
  8 elements array take 3 steps, 32 elements array takes 5 steps
  Each time we decompose it, during merging we have O(n) comparisions.
  Hence O(log n) decompositions * O(n) comparision per decomposition

Implementation

// Merge sort implementation

function mergeSort(arr) {
  if (arr.length <= 1) return arr;
  let mid = Math.floor(arr.length / 2);
  let left = mergeSort(arr.slice(0, mid));
  let right = mergeSort(arr.slice(mid));
  return merge(left, right);
}

// Merging two sorted arrays - merge([1, 10, 50], [2, 14, 99, 100]) merge([1, 2, 50], [3, 7, 99, 100])
function merge(a = [], b = []) {
  const sorted = [];
  let i = 0;
  let j = 0;
  while (a[i] && b[j]) {
    if (a[i] <= b[j]) {
      sorted.push(a[i]);
      i++;
    } else {
      sorted.push(b[j]);
      j++;
    }
  }
  while (a[i]) {
    sorted.push(a[i]);
    i++;
  }
  while (b[j]) {
    sorted.push(b[j]);
    j++;
  }
  return sorted;
}

---

Quick Sort

• Like Merge sort it uses the fact that an array with 0 or 1 element is already sorted
• Works by selecting one element called pivot and finding the index where pivot should be in sorted array
• After finding a pivot, move all the numbers less then that no to the left and all the no greater to the right (order doesnt matter)
• After one pass, we know that that pivot is in the right spot
• Repeat the process for left side and then right side
• Runtime of quick sort changes on how one selects a pivot
• Ideally pivot should be the median value of the data
• Since sorting is happening in place, base condition of recursion is not that array has 0 or 1 element, rather subarray has 0 or 1 elements
• Time complexity of Quick sort is O(n log n) for best and avg case, O(n * n) for worst case
• In worst case is an already sorted array, hence instead of picking first item as a pivot, pick middle or a random element
• Space complexity is O(n log n)

Implementation

/* Pivot helper function
This function should designate an element as pivot and rearrange elements such that values less then pivot are to the left and greater to the right
The order of values on either side doesnt matter
Should do this in place, DO NOT create new array
when done return the index of the pivot
*/

function pivot(arr = [], start = 0, end = arr.length - 1) {
  let pivot = arr[start];
  let smallerCount = 0;
  let swapTo = start + 1;
  for (let i = start; i <= end; i++) {
    if (arr[i] < pivot) {
      smallerCount++;
      [arr[swapTo], arr[i]] = [arr[i], arr[swapTo]];
      swapTo++;
    }
  }
  [arr[smallerCount], arr[start]] = [arr[start], arr[smallerCount]];
  console.log("-arr-", arr);
  return smallerCount;
}

// Quick sort implementation
function quickSort(arr, left = 0, right = arr.length - 1) {
  if (left < right) {
    let pivotIndex = pivot(arr, left, right);
    quickSort(arr, left, pivotIndex - 1);
    quickSort(arr, pivotIndex + 1, right);
  }
  return arr;
}

/* 
Shorter explanation : 
[4, 8, 2, 1, 5, 7, 6, 3]
4 is selected as first pivot, array gets divided as left partition [3, 2, 1] and right partition [5, 7, 6, 8]
we work on left partition [3, 2, 1] first, 3 is selected as pivot, array gets divided as left partition [1, 2]
we work on left partition [1, 2], 1 is selected as pivot, left side sorting done [1, 2, 3]
we work on right partition [5, 7, 6, 8] now, 5 is selected as pivot, array gets divided as right partition [7, 6, 8]
we work on right partition [7, 6, 8] now, 7 is selected as pivot, array gets divided as left partition [6] and right partition [8]
we work on left partition [6] first
we work on right partition [8] now
list is sorted [1, 2, 3, 4, 5, 6, 7, 8]

This is a DFS approach, we use stack for DFS, in this case we use recursion, which uses the call stack
*/

---

Heap Sort

Heap sort is a comparison-based sorting algorithm that uses a binary heap data structure to build a max-heap or min-heap. In the case of heap sort, it typically builds a max-heap to sort the elements in ascending order.

• The time complexity of heap sort is O(n log n) for the worst, average, and best cases.
• The Space Complexity is O(1) - In-place sorting algorithm, uses only a constant amount of additional memory.
• The best-case scenario for heap sort occurs when the input array is already sorted.
• The worst-case scenario for heap sort occurs when the input array is in reverse order, and the heapification process is required for every element.

Steps:

1. Build a Max-Heap : Convert the given array into a max-heap, This involves rearranging the array elements so that they satisfy the max-heap property: the value of each node is greater than or equal to the values of its children.

2. Heapify : Start from the last non-leaf node (i.e., the last node with children) and heapify each subtree in reverse order.
   The heapify operation ensures that the largest element is at the root of the max-heap.
   For each node, compare it with its children. If any child is greater, swap the node with the larger child. Repeat this process recursively until the entire heap is valid.

3. Extract Max and Rebuild Heap : After building the max-heap, the largest element (at the root) is swapped with the last element of the array.
   The size of the heap is reduced by 1 (excluding the last element that is now part of the sorted array).
   The max-heap property is restored by heapifying the root.

4. Repeat Steps 3 Until Heap is Empty : At each step, the maximum element is extracted and placed at the end of the array.

   function heapSort(arr) {
     // Build max heap
     for (let i = Math.floor(arr.length / 2) - 1; i >= 0; i--) {
       heapify(arr, arr.length, i);
     }
   
     // Extract elements from the heap
     for (let i = arr.length - 1; i > 0; i--) {
       // Swap the root (maximum element) with the last element
       [arr[0], arr[i]] = [arr[i], arr[0]];
   
       // Heapify the reduced heap
       heapify(arr, i, 0);
     }
   }
   
   function heapify(arr, n, i) {
     let largest = i;
     const left = 2 * i + 1;
     const right = 2 * i + 2;
   
     // Compare with left child
     if (left < n && arr[left] > arr[largest]) {
       largest = left;
     }
   
     // Compare with right child
     if (right < n && arr[right] > arr[largest]) {
       largest = right;
     }
   
     // Swap and continue heapifying if needed
     if (largest !== i) {
       [arr[i], arr[largest]] = [arr[largest], arr[i]];
       heapify(arr, n, largest);
     }
   }
   
   // Example usage:
   let myArray = [12, 11, 13, 5, 6, 7];
   heapSort(myArray);
   console.log("Sorted array:", myArray);

---

Radix Sort

Instead of making comparisions, it uses no of digits and places them into buckets

• All the above sorting algorithms are comparision sorts, at the base we compare two elements at once
• The best comparision sorts can do is O(n log n), which is in accordance to mathematical bounds
• There are other type of sorting algorithms that do not use comparision, they take advantage of special properties of data, One of them is Radix Sort
• For eg - there is a group of sort called integer sorting algorithms
• Radix sort is a special sorting algorithm that does not use comparisions and works on lists of numbers
• It uses the fact that information about the size of a number is encoded in the number of digits (More digits means a bigger no !!)
• Time complexity is O(nk) where k is word size of nos
• Space complexity is O(n + k)

Radix sort Working

• Form 10 buckets labelled from 0 to 9, incase the base is 10
• If base of nos is 2, buckets will be 0 and 1
• check the units place of all the numbers in the array, and place them accordingly into the buckets
• ex - 45677 will go into 7, 40 will go into 0, 7 will go into 7, etc
• now maintain the order in which they were in the buckets
• now place them again in buckets , by checking tens place
• ex- 45677 will go in 7, 40 will go in 4 , 567 will go in 6
• repeat till the the first digit of the longest no is compared

Radix sort Implementation

radixSort

---

Count Sort

Useful only when you know the range of data and the range is not very high ( < 10 ^ 6)

• Consider you want to sort an array [5,3,3,7,2,9], here all numbers are in range 0 - 10
• Create an array 'frequency' of length = range max value, with all elements as 0 , frequency = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
• Loop over input array and increase frequency by 1 at index = value, frequency = [0, 0, 1, 2, 0, 1, 0, 1, 0, 1]
• Create new array 'sortedArray', Loop over frequency array and push index where frequency[index] > 0, if frequency[index] > 1 push for frequency[index] times
• sortedArray = [2, 3, 3, 5, 7, 9]

// Count Sort implementation

const countSort = (arr = [], range = 100) => {
  const sortedArray = [];
  let frequency = new Array(range);

  for (let i = 0; i < range; i++) frequency[i] = 0;
  arr.forEach((item) => (frequency[item] += 1));

  for (let i = 0; i < frequency.length; i++) {
    while (frequency[i] > 0) {
      sortedArray.push(i);
      frequency[i]--;
    }
  }
  return sortedArray;
};

---

Comparision of sorting algorithms

• Bubble sort, Selection sort, Insertion sort work well with shorter arrays and have nearly the same complexities O(n * n)
• Bubble sort and Insertion sort works well with nearly sorted data , O(n)
• Selection sort takes too long to sort nearly sorted data, O(n*n), as still have to loop all the way to find the min value
• Insertion sort can handle new values being pushed at the end of the array
• Merge sort has time complexity O(n log n) and space complexity is O(n)
• Time complexity of Quick sort is O(n log n) for best and avg case, O(n * n) for worst case and
• Space complexity of Quick sort is O(n log n)
• There are other type of sorting algorithms that do not use comparision, they take advantage of special properties of data, One of them is Radix Sort
• Time complexity of radix sort is O(nk) where k is word size of nos and Space complexity is O(n + k)

---

Data Structures

Data structures are collections of values, the relationship among then, and the functions or operations that can be applied to the data

Classes and Instances

Class

• A blueprint for creating objects with predefined properties and methods, like making a mould
• class names conventionally start with capital letters
• Constructor is a special function that runs when the class is instantiated
• The class keyword creates a constant so you cannot redefine it
• class instances are created using the new keyword

class Student() {
  constructor(firstName, lastName) {
    this.firstName = firstName;
    this.lastName = lastName;
  }
}

let pooja = new Student('Pooja', 'patel');
console.log(pooja.firstName);

Instance Methods

• Methods that work on individual instance level, and not class level

class Student() {
  constructor(firstName, lastName) {
    this.firstName = firstName;
    this.lastName = lastName;
  }
  fullName() {
    return `Your full name is ${this.firstName} ${this.lastName}`;
  }
}

let pooja = new Student('Pooja', 'patel');
pooja.fullName()

Class Methods

• Methods that is relevent to class, but not necessarily to individual instances
• we use static keyword in front of method defination
• static methods are called without instantiating thier class and cannot be called through a class instance
• static methods are often used to create utility functions for an application

class Student() {
  constructor(firstName, lastName) {
    this.firstName = firstName;
    this.lastName = lastName;
  }
  fullName() {
    return `Your full name is ${this.firstName} ${this.lastName}`;
  }
  static enrollStudents(...students) {
    // send email to students
  }
}

let pooja = new Student('Pooja', 'patel');
Student.enrollStudents([pooja]);

• Use case of a class method

class Point {
  constructor(x, y) {
    this.x = x;
    this.y = y;
  }

  static calculateDistance(a, b) {
    const dx = a.x - b.x;
    const dy = a.y - b.y;
    return Math.hypot(dx, dy);
  }
}

const p1 = new Point(5, 5);
const p2 = new Point(10, 10);

Point.calculateDistance(p1, p2);

• here each point represents a point in x,y cordinate system
• To calculate distance between two points, it does not make much sense to call distance on a single point
• Can be implemented like p1.calculateDistance(p2) but since it is more of a utility function, we make it a class method

---

Singly Linked Lists

Linked Lists consists of nodes, each node has a value and a pointer to the next node

Arrays are like elevators we can go from 6th floor to the 99th, Linked Lists are like stairs we need to go through 1, 2 to reach 3

• In array each item is mapped to its index with a no, i can get the 5th item of an array
• Linked list consist of elements with no indexes, just pointing to another element, like a train
• Each element is called a node, a node has a value and a pointer to the next node or null
• we keep track of three properties - head, tail , length

Pros and Cons

• Inserting and deleting to the start of array invloves shifting every element, in linked list its just to add an element and point to previos head
• Random access is not possible in linked lists

// creating a Node class
class Node{
  constructor(val) {
    this.val = val;
    this.next = null;
  }
}

const a = new Node(5);
a.next = new Node(10);
a.next.next = new Node(15);

// console.log(a) is
Node {
  val: 5,
  next: Node { val: 10, next: Node { val: 15, next: null } }
}

// create a class for singlyLinkedList and add push method to it

class SinglyLinkedList {
  constructor() {
    this.head = null;
    this.tail = null;
    this.length = 0;
  }
  push(val) {
    // if no node add node and set is as head, tail and length ++
    // if nodes present, add new node, set next of previous node as this node, set this node as tail, length ++
    if (this.length) {
      const node = new Node(val);
      this.tail.next = node;
      this.tail = node;
    } else {
      const node = new Node(val);
      this.head = node;
      this.tail = node;
    }
    this.length += 1;
    return this;
  }
}

const a = new SinglyLinkedList();
a.push(5);
a.push(10);
console.log(a);

Traverse

traverse() {
  let node = this.head;
  while(node){
    console.log(node.val);
    node = node.next;
  }
}

Pop

pop() {
  // find out the secondLastNode, set its next to null, set it as tail return last node, length --
  if(!this.head) return undefined;
  let node = this.head;
  let secondLastNode = null;
  while(node.next){
    secondLastNode = node;
    node = node.next;
  }
  secondLastNode.next = null;
  this.tail = secondLastNode;
  this.length -= 1;
  return node;
}

Shift

shift() {
    // set head as head.next, length--
    if(!this.head) return undefined;
    const currentHead = this.head;
    this.head = this.head.next;
    this.length -= 1;
    if(this.length === 0) {
      this.tail = null;
    }
    return currentHead;
  }

Unshift

unshift(val) {
  // set next of this node as existing head, set this node as head, length++
  const newNode = new Node(val);
  newNode.next = this.head;
  this.head = newNode;
  this.length += 1;
  if(this.length === 1) {
    this.tail = newNode;
  }
  return newNode;
}

Search

search(val) {
  if(val < 0) return null;
  let counter = 0;
  let node = this.head;
  while(node && node.val !== val){
    counter ++;
    node = node.next;
  }
  if(node === null) {
    return null;
  }
  return counter;
}

Get

get(index) {
  if(index < 0) return null;
  let counter = 0;
  let node = this.head;
  while(node && counter !== index){
    node = node.next;
    counter++;
  }
  return node;
}

Set

set(index, value) {
  let node = this.get(index);
  if(!node) return null;
  node.val = value;
  return node;
}

Insert

insert(index, value) {
  if(index < 0) return null;
  if(index === 0) return this.unshift(value);
  const node = this.get(index-1);
  const newNode = new Node(value);
  newNode.next = node.next;
  node.next = newNode;
  this.length++;
  return this;
}

Remove

remove(index){
  if(index < 0) return null;
  if(index === 0) return this.shift();
  const node = this.get(index);
  const prevNode = this.get(index - 1);
  prevNode.next = node.next;
  this.length--;
  return node;
}

Reverse

// reverse linked list in place
reverse(){
  let node = this.head;
  this.head = this.tail;
  this.tail = node;
  let next = null;
  let prev = null;
  for(var i =0; i<this.length ; i++){
    next = node.next;
    node.next = prev;
    prev = node;
    node = next;
  }
  return this;
}

Reverse a single linked list

reverse() {
  if(!this.head){
    return this.head;
  }
  let previousChain = null;
  let current = this.head;
  let nextChain = current.next;
  while(current){
    nextChain = current.next;
    current.next = previousChain;
    previousChain = current;
    current = nextChain;
  }
  return previousChain;
}

// Todo expand and explain

BigO of Singly Linked Lists

• Insertion at start or end is O(1), for array its O(n) for start and O(1) for end
• Removal from start is O(1) from end O(n), in array removal from start is O(n) and from end is O(1)
• searching is O(n), for array too its O(n)
• Accessing is O(n), for arrays it is O(1)

Leetcode problems

Reverse linked list
Reverse linked list partially linked list cycle

---

Doubly Linked Lists

class Node {
  constructor(data) {
    this.data = data;
    this.prev = null;
    this.next = null;
  }
}

class DoublyLinkedList {
  constructor() {
    this.head = null;
    this.tail = null;
  }

  // Add a node to the end of the list
  append(data) {
    const newNode = new Node(data);

    if (!this.head) {
      // If the list is empty, set the new node as the head and tail
      this.head = newNode;
      this.tail = newNode;
    } else {
      // Otherwise, add the new node to the end and update pointers
      newNode.prev = this.tail;
      this.tail.next = newNode;
      this.tail = newNode;
    }
  }

  // Add a node to the beginning of the list
  prepend(data) {
    const newNode = new Node(data);

    if (!this.head) {
      // If the list is empty, set the new node as the head and tail
      this.head = newNode;
      this.tail = newNode;
    } else {
      // Otherwise, add the new node to the beginning and update pointers
      newNode.next = this.head;
      this.head.prev = newNode;
      this.head = newNode;
    }
  }

  // Display the elements of the list
  display() {
    let current = this.head;
    while (current) {
      console.log(current.data);
      current = current.next;
    }
  }

  // Reverse the doubly linked list
  reverse() {
    let current = this.head;
    let temp = null;

    // Swap the prev and next pointers for each node
    while (current) {
      temp = current.prev;
      current.prev = current.next;
      current.next = temp;

      current = current.prev; // Move to the next node
    }

    // Swap the head and tail pointers
    temp = this.head;
    this.head = this.tail;
    this.tail = temp;
  }
}

// Example usage:
const doublyList = new DoublyLinkedList();
doublyList.append(1);
doublyList.append(2);
doublyList.append(3);
doublyList.prepend(0);
console.log("Original Doubly Linked List:");
doublyList.display();

console.log("\nReversed Doubly Linked List:");
doublyList.reverse();
doublyList.display();

Leetcode problems

For some sliding window problems, where you need to move the window and remove and add elements from either side, consider using a double-ended-queue

Sliding window max

---

Stack and Queues

Stack is an abstract data structure, that uses LIFO principle, last item in comes out first. Real world examples would be call stack of the browser, stack of books, or plates, etc.

Queue is an abstract data structure, that uses FIFO principle, first item in comes out first. Real world examples would be queues at ticket counter, etc.

• Stacks are used in browsers call stack, and managing function invocation
• Stacks are also used in Undo/Redo
• Routing and managing history in browsers use stacks
• Queues are used in games, where the one waiting from longest is added first
• Queues are used in background downloading or uploading
• Queues are used by printer to decide which doc to print first

BigO of Stacks and Queues

• Insertion in stack is O(1), for queue using linkedLists is O(1) but using array is O(n)
• Removal in stack is O(1), for queue using linkedLists is O(1) but using array is O(n)
• Searching in stack and queue is O(n)
• Access in stack and queue is O(n)

Implementation of Stack and queues

• In JavaScript, you can implement stacks and queues using arrays or linked lists
• stack implementation using array
• queue implementation using linked list

Leetcode problems

HTML Elements

---

Binary Search Tree

Trees are non linear data structures, which has nodes in a parent-child relationship

Binary Trees are special types of trees, in which each node can have atmost 2 childrens

Binary Search Trees are special type of Binary trees, where Every node to the left of parent is always less then the parent and every node to the right of parent is always greater then the parent

Trees

• Trees are non linear data structures, which has nodes in a parent-child relationship
• Nodes in trees can point to multiple nodes, unlike linked lists or doubly linked lists
• Lists are linear, every thing is in a row
• Trees are non linear, they can branch
• we have more then one pathway to a tree
• Singly linked list can be considered as a very special case of a tree where every parent has exactly one child

Tree Terminology

• Root - starting topmost node of a tree
• Parent - Any node that has child nodes
• Child - Any node that a parent points to
• Leaf - A child node that doesnt point to any other nodes
• Edge - connects two nodes

Rules for a valid tree

• A tree should have only one root node
• Siblings cannot point to each other in a tree
• Child cannot point to parent or parents siblings

Real World use cases

• HTML DOM structure is a tree structure
• Network routing distributions like Broadcast, multicast, geocast
• Linting softwares use trees
• AI applications - like miniMax tree used by tic-tac-toe
• Folders in operating systems
• JSON has tree structure

Binary Search Trees

• Binary Trees are special types of trees, in which each node can have atmost 2 childrens
• Binary Search Trees are special type of Binary trees, they excel at searching
• Binary Search Trees are used to store data that can be compared ie sortable
• If we take any node, every no less then that are located to the left side, every no greater then that are located to the right
• Every node to the left of parent is always less then the parent
• Every node to the right of parent is always greater then the parent

class Node {
  constructor(value) {
    this.value = value;
    this.left = null;
    this.right = null;
  }
}

class BinarySearchTree {
  constructor() {
    this.root = null;
  }
}

/*
BinarySearchTree {
root: Node {
  value: 10,
  left: Node { value: 7, left: [Node], right: null },
  right: Node { value: 15, left: null, right: [Node] }
}
}
*/

// if no root assign value as root
// decide left or right
// if no left or right, assign it as left or right node
insert(value){
  if(!this.root){
    this.root = new Node(value);
    return this;
  }
  let node = this.root;
  while(node){
    if(value === node.value) return undefined;
    if(value<node.value){
      if(!node.left){
        node.left = new Node(value);
        return this;
      }
      node = node.left;
    }
    else {
      if(!node.right){
        node.right = new Node(value);
        return this;
      }
      node = node.right;
    }
  }
}

find(value){
  if(!this.root) return null;
  let node = this.root;
  while(node){
    if(value === node.value) return true;
    if(value < node.value){
      node = node.left;
    } else {
      node = node.right;
    }
  }
  return false;
}

BigO of Binary Search Trees

• Insertion and searching is O(log n) though there are some exceptions
• Eg 3 -> 17 -> 19 -> 32 -> 63 -> 91

Leetcode problems

Diameter of binary trees

---

Tree Traversal

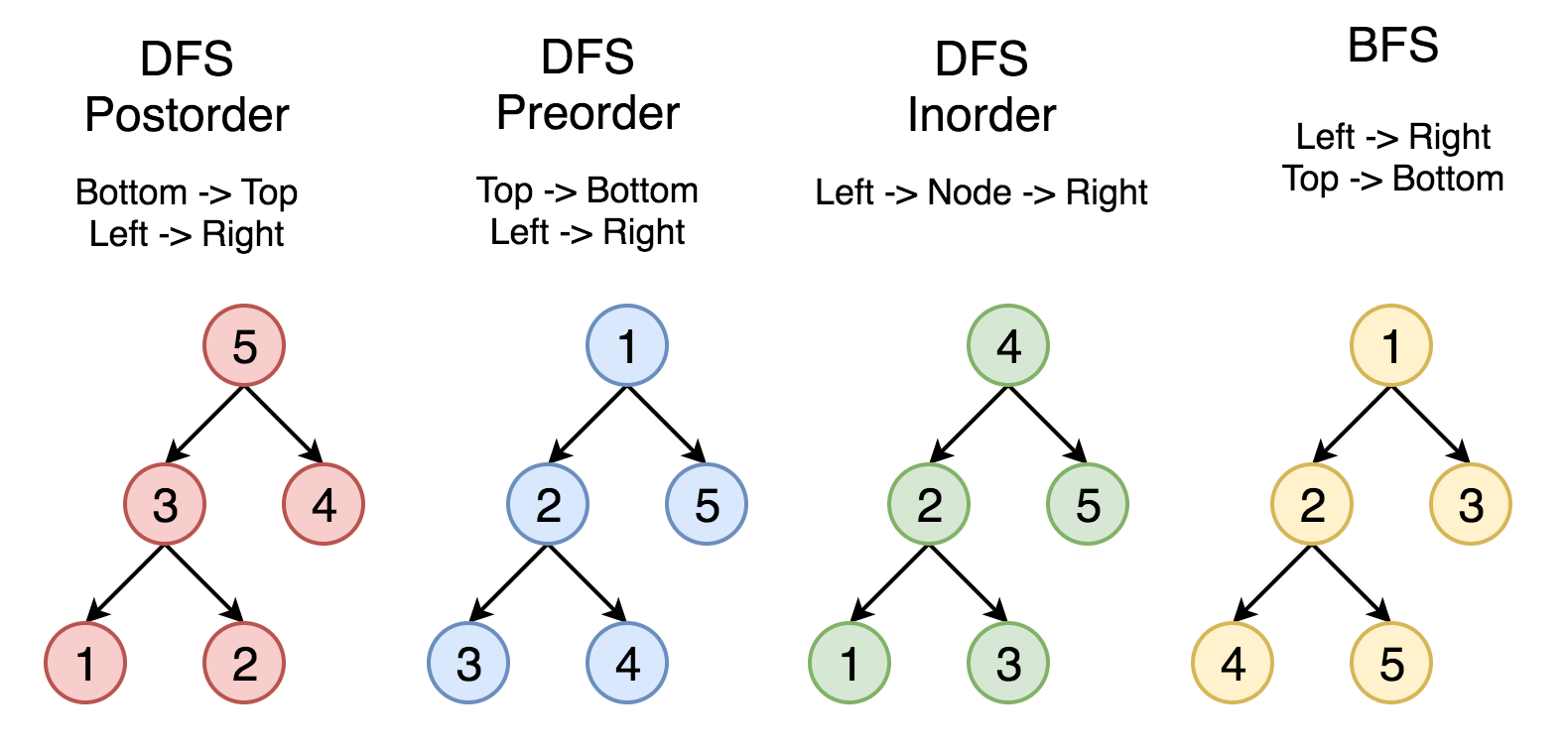
Tree Traversal - Given any generic tree, how do we visit every node atleast one time

Two Ways of Tree Traversal

1. Breadth First Search (BFS)
2. Depth First Search (DFS)
   1. PreOrder DFS
   2. InOrder DFS
   3. PostOrder DFS

Consider a tree

                10
            6       15
          3   8         20

Breadth First Search (BFS)

• We use queue to manage nodes to be visited
• Whenever a node is visited we push its left and right to the queue, they are checked according to FIFO

// place root node in queue
// while anything in queue
// take first element out and put in visited
// check if it has left add that in queue, check if right put it in queue
breadthFirstSearch(){
  let queue = [];
  let visited = [];
  queue.push(this.root);
  while(queue.length){
    const node = queue.shift();
    visited.push(node.value);
    if(node.left){
      queue.push(node.left);
    }
    if(node.right){
      queue.push(node.right);
    }
  }
  return visited;
}

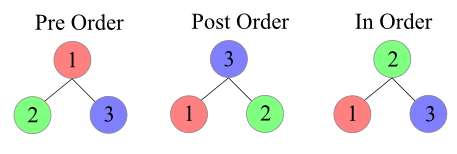
// [10, 6, 15, 3, 8, 20]

Depth First Search (DFS)

• PreOrder - Root Left Right
• InOrder - Left Root Right
• PostOrder - Left Right Root

Recursievely call helper function
PreOrder

// root left right
preOrderDFS(){
  const result = [];
  function traverse(node){
    result.push(node.value);
    if(node.left) traverse(node.left);
    if(node.right) traverse(node.right);
  }
  traverse(this.root);
  return result;
}
// [10,6,3,8,15,20]

InOrder

// left root right
inOrderDFS(){
  const result = [];
  function traverse(node){
    if(node.left) traverse(node.left);
    result.push(node.value);
    if(node.right) traverse(node.right);
  }
  traverse(this.root);
  return result;
}
// [3,6,8,10,15,20]

PostOrder

// left right root
postOrderDFS(){
  const result = [];
  function traverse(node){
    if(node.left) traverse(node.left);
    if(node.right) traverse(node.right);
    result.push(node.value);
  }
  traverse(this.root);
  return result;
}
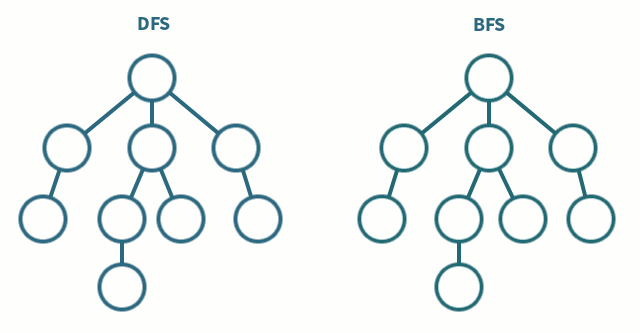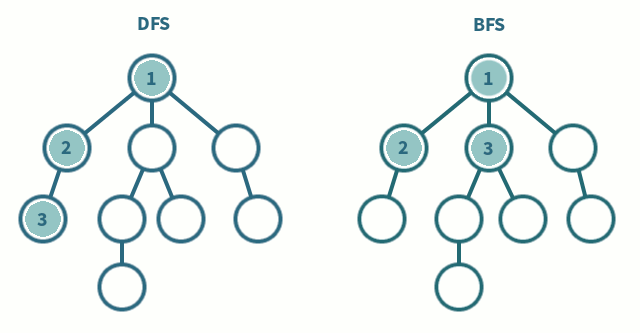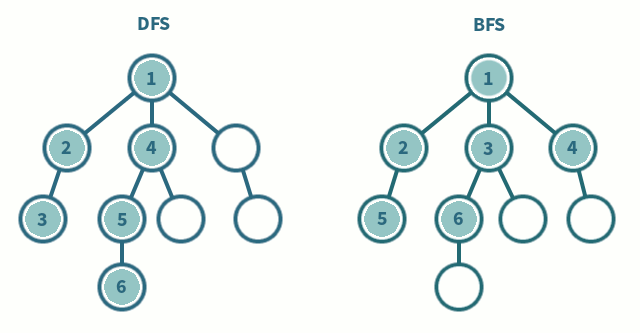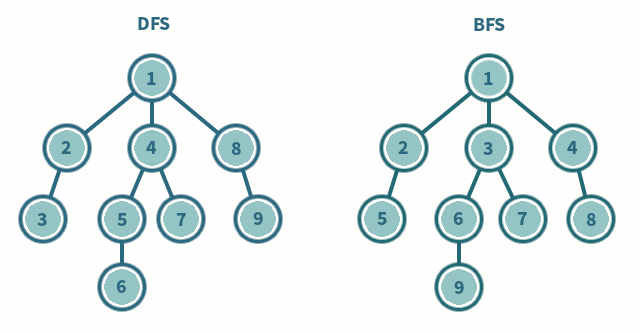
// [3,8,6,20,15,10]

Comparision of BFS, PreOrder DFS, InOrder DFS, PostOrder DFS

Traversing a Tree using BFS, PreOrder DFS, InOrder DFS, PostOrder DFS

                10
            6       15
          3   8         20


  BFS [10, 6, 15, 3, 8, 20]
  PreOrder DFS = [10,6,3,8,15,20]
  InOrder DFS = [3,6,8,10,15,20]
  PostOrder DFS = [3,8,6,20,15,10]

When to use BFS and DFS

• Time commplexity of BFS and DFS is the same
• If a tree is has 100 level depth, traversing using BFS will take a lot more space, as the queue will hold too many lefts and rights which itself are nested
• For deep trees using DFS is ideal
• For a tree that look likes linked list, BFS queue will always have one thing at a time in queue, using DFS in such cases will take up more space in call stack
• For a Binary search tree, InOrder traversal we get all nodes in underlying order, like arrows bringing them all down
• In such cases InOrder returns like sorted array
• PreOrder can be used to export a binary tree and can be easily reconstructed

---

Binary Heaps

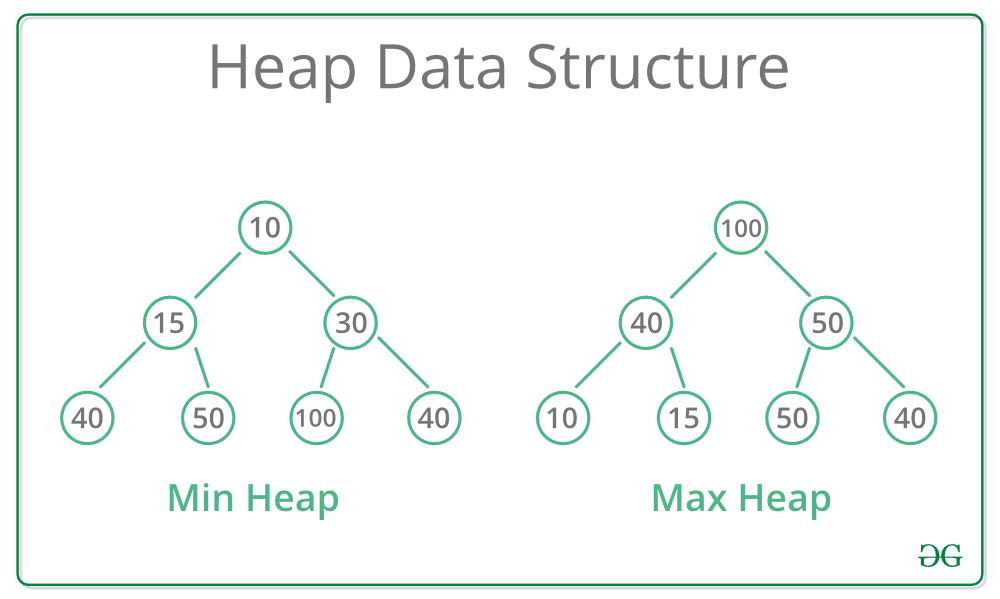
Heap is a special case of balanced binary tree, where the root-node key is compared with its children and arranged accordingly

Balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1

Heaps can be of two types:

1. Max-Heap
   In a Max-Heap the key present at the root node must be greatest among the keys present at all of it’s children.
   The same property must be recursively true for all sub-trees in that Binary Tree.
2. Min-Heap
   In a Min-Heap the key present at the root node must be minimum among the keys present at all of it’s children.
   The same property must be recursively true for all sub-trees in that Binary Tree

Max Binary Heap

• Since Binary, each parent has at most two children
• Since Max, value of each parent node is greater then its children
• no guarantees between siblings
• Is as compact as possible, Every left and right is filled before we move down
• left children are filled out first

Use of Heaps

• Binary heaps are used to implement priority queues
• Binary heaps are used with graph traversal algorithms

Representing a Heap

• Heaps are represented by arrays
• For any index n, its left child is stored at 2n+1 and right child at 2n+2
• Eg - 12 is on index 4, so its childern are on index 9 and 10, values 6 and 11
• For an index n, its parent is at (n-1)/2
• Eg - 1 is on index 13, so 13-1/2 ie 6 th index is its parent with value 5

Inserting to a MaxBinaryHeap

1. Push to the empty right node or left most node(end of the array)
2. If the value is not in its correct position, ie value greater then its parent, we bubble up
3. while the value is greater then its parent, swap it with parent

insert(value){
  this.values.push(value);
  this.bubbleUp();
}
bubbleUp(){
  let index = this.values.length -1;
  let value = this.values[index];
  while(index > 0){
    let parentIndex = Math.floor((index-1)/2);
    let parent = this.values[parentIndex];
    if(value <= parent) break;
    this.values[parentIndex] = value;
    this.values[index] = parent;
    index = parentIndex;
  }
}

Down Heap/Bubble Down

The process of deleting the root from the heap and and restoring the properties is known as down-heap, bubble-down, cascade-down, extract min/max.

1. Remove the Root
2. Swap with the most recently added
3. Bubble Down

extractMax(){
  const max = this.values[0];
  const mostRecent = this.values.pop();
  if(this.values.length) {
    this.values[0] = mostRecent;
    this.bubbleDown();
  }
  return max;
}
bubbleDown(){
  let n = 0;
  const element = this.values[0];
  while(true){
    let leftIndex = (2*n)+1;
    let rightIndex = (2*n)+2;
    let swap = false;
    let maxIndex = this.values[leftIndex] > this.values[rightIndex] ? leftIndex : rightIndex;
    if(this.values[n] < this.values[maxIndex]){
      swap = true;
      this.values[n] = this.values[maxIndex];
      this.values[maxIndex] = element;
      n = maxIndex;
    }
    if(!swap) break;
  }
}

console.log(heap.values); // [55, 39, 41, 18, 27, 12, 33]
console.log(heap.extractMax()); // 55
console.log(heap.values); // [ 41, 39, 33, 18, 27, 12 ]

Bubble up

• To add a value to a heap - Add to the end of the tree (last element in array), bubble up
• Bubble up means to start comparing from leaf nodes to the root node (end to array to start of array), so the loop condition will be till index > 0
• Since the rest of the max heap is already following conditions, and only the inserted element might be at wrong position, we do not need to check condition for all index from n to 1
• We just compare last element to parent, and swap if needed, then the parent element to its parent and so on. If we did not need to swap at any stage, it means that the element is at its correct position, and we can break from the loop

Bubble down

• To remove max value from a heap - Swap the root and the last leaf node, remove the last lead node ie the root
• Now since lower value is moved to the root, start swapping from root to the leaf nodes, This is called bubble down
• start comparing from root node to leaf nodes (start of array to end of array), so the loop condition will be index < length
• Since the rest of the max heap is already following conditions, and only the root element might be at wrong position, we do not need to check condition for all index from 0 to n
• We just compare root element to its children, and swap if needed, then the child element to its child and so on. If we did not need to swap at any stage, it means that the element is at its correct position, and we can break from the loop

BigO of Binary Heaps

• Time complexity for Insertion - O(log n)
• Time complexity for Removal - O(log n)
• Time complexity for Searching - O(n/2) -> O(n)

Leetcode problems

Last stone weight Task scheduler

Priority Queue

Priority Queue is an abstract data structure, in which each element has an associated priority.
They are mostly implemented using min heaps

• A lower number indicates a higher priority
• Priority queues are used in medical emergency management, used by operating systems to prioritize processes
• Implementing priority Queue using heaps, time complexity is O(log n), as compared to arrays that would be O(n)
• The element with higest priority is taken out first and the rest are bubbled down

Implementation using min heaps

class Node {
  constructor(value, priority) {
    this.value = value;
    this.priority = priority;
  }
}

class PriorityQueue {
  constructor() {
    this.values = [];
  }

  enqueue(node) {
    this.values.push(node);
    this.bubbleUp();
  }
  bubbleUp() {
    let index = this.values.length - 1;
    let node = this.values[index];
    while (index > 0) {
      let parentIndex = Math.floor((index - 1) / 2);
      let parentNode = this.values[parentIndex];
      if (node.priority >= parentNode.priority) break;
      this.values[parentIndex] = node;
      this.values[index] = parentNode;
      index = parentIndex;
    }
  }
}

const hospitalQueue = new PriorityQueue();
hospitalQueue.enqueue(new Node("low fever", 5));
/*
PriorityQueue {
  values: [
    Node { value: 'broken head', priority: 1 },
    Node { value: 'heart attack', priority: 3 },
    Node { value: 'accident', priority: 2 },
    Node { value: 'flu', priority: 7 },
    Node { value: 'low fever', priority: 5 },
    Node { value: 'concussion', priority: 4 },
    Node { value: 'head ache', priority: 6 }
  ]
}
*/

dequeue(){
  const higestPriority = this.values[0];
  const end = this.values.pop();
  if(this.values.length){
    this.values[0] = end;
    this.bubbleDown();
  }
  return higestPriority;
}
bubbleDown(){
  let index = 0;
  const node = this.values[index];
  while(true){
    let swap = false;
    let leftChildIndex = (2*index)+1;
    let rightChildIndex = (2*index)+2;
    let swapIndex = (rightChildIndex < this.values.length) && (this.values[rightChildIndex].priority < this.values[leftChildIndex].priority)
      ? rightChildIndex : leftChildIndex;
    if(swapIndex < this.values.length && node.priority > this.values[swapIndex].priority){
      swap = true;
      this.values[index] = this.values[swapIndex];
      this.values[swapIndex] = node;
      index = swapIndex;
    }
    if(!swap) break;
  }
}

/*
PriorityQueue {
  values: [
    Node { value: 'accident', priority: 2 },
    Node { value: 'heart attack', priority: 3 },
    Node { value: 'concussion', priority: 4 },
    Node { value: 'flu', priority: 7 },
    Node { value: 'low fever', priority: 5 },
    Node { value: 'head ache', priority: 6 }
  ]
}
*/

BigO of Priority Queue using Heaps

• Time complexity for Insertion - O(log n)
• Time complexity for Removal - O(log n)
• Time complexity for Searching - O(n/2) -> O(n)

---

Hash Table/Hash Map

Hash maps are used to store key-value pairs, the keys are not ordered and can be of any type string, number, etc

• Hashmaps are fast for all operations like inserttion, removal, access
• Hashmaps unlike other data structures are builtin in most programming languages
• Python has Dictionaries
• js has Objects and Maps
• java go and scala have Maps
• Ruby has Hashes

Understanding how hashing works behind the scene, implemention own key-value pair ds

• To implement our hash map, we will use arrays, and save our color values from 0 to 9
• To lookup values by keys like 'pink' we need to convert it to valid array indices like 3
• A function that converts keys to array indexes is called a hash function
• A hash function should return the same index for a given key, every time it is called

Hash Function

A Function that takes in an input of arbitary size and gives output of a fixed size

• Hash function are used in Hashmaps, cryptography, caches, protecting data, etc

What makes a good hash function

• Fast (constant time)
• Distributes uniformly
• Deterministic (same input generates same output)
• Doesnt work other way (should not tell what input generated a specific output)

Writing our Hash Function

1. To convert 'pink' to some number we can add the character codes of all digits

   "pink".charCodeAt(0); // 112 char code of p
   "pink".charCodeAt(1); // 105 char code of i
   "a".charCodeAt(0) - 96; // 1 place of a in alphabets
   "p".charCodeAt(0) - 16; // 16 place of p in alphabets

2. Adding places in alphabets gives 16+9+14+11 = 40, We need a value between 0 to 9

3. To restrict number to a limit we use modulo operator, which gives remainder

4. A remainder is always less then the divisor, 40%9 is 4

   function hash(key, limit = 100) {
     let total = 0;
     for (var i of key) {
       total += i.charCodeAt(0) - 96;
     }
     return total % limit;
   }
   
   console.log(hash("pink", 10)); // 0
   console.log(hash("cyan", 10)); // 3
   console.log(hash("maroon", 10)); // 6
   console.log(hash("orange", 10)); // 0

5. Problems with this function - We get same value for 'pink' and 'orange', O(n) not constant time

6. To Spread out keys more Uniformly we will use prime nos

7. It is also very helpful if the array's length we are putting values in is a prime no

8. Observations from an exp hashing 10million pairs of data using different sizes of lists
   length of 8191(prime no) --> 1.92 collisions while 8192(non prime) ---> 3510 collision

   function hash(key, limit = 100) {
     let total = 0;
     let PRIME = 31;
     for (var i = 0; i < Math.min(key.length, 100); i++) {
       let value = key[i].charCodeAt(0) - 96;
       total = (total * PRIME + value) % limit;
     }
     return total % limit;
   }

Dealing with collisions

Collision happens when multiple keys hash to the same bucket, that is distinct keys produce the same hashCode value

1. Seperate Chaining

   Store data using nested arrays or linkedList and directly look into the nested structure by key

2. Linear Probing

   In case two keys generate same hash, the first one would be stored at the hash position, and the other one(s) would be stored at next empty position

Implementing hashmap using seperate chaining

class Hashmap {
  constructor(size = 53) {
    this.keyValues = new Array(size);
  }
  hash(key) {
    let total = 0;
    let PRIME = 31;
    for (var i = 0; i < key.length; i++) {
      let value = key[i].charCodeAt(0) - 96;
      total = (total * PRIME + value) % this.keyValues.length;
    }
    return total % this.keyValues.length;
  }
  set(key, value) {
    const hash = this.hash(key);
    if (!this.keyValues[hash]) {
      this.keyValues[hash] = [];
    }
    this.keyValues[hash].push([key, value]);
  }
  get(key) {
    const hash = this.hash(key);
    if (this.keyValues[hash]) {
      if (
        this.keyValues[hash].length === 1 &&
        this.keyValues[hash][0][0] === key
      )
        return this.keyValues[hash][0][1];
      for (let i = 0; i < this.keyValues[hash].length; i++) {
        if (this.keyValues[hash][i][0] === key)
          return this.keyValues[hash][i][1];
      }
    }
    return undefined;
  }
}

const hashmap = new Hashmap(13);
hashmap.set("pink", "#765678");
hashmap.set("green", "#68bt56");
hashmap.set("orange", "#tndu74");
hashmap.set("cyan", "#678765");
hashmap.set("maroon", "#878787");
hashmap.set("red", "#879098");
console.log("%j", hashmap);
// {"keyValues":[null,null,null,[["green","#68bt56"]],null,[["pink","#765678"],["cyan","#678765"]],null,null,null,null,[["orange","#tndu74"]],[["maroon","#878787"],["red","#879098"]],null]}
console.log(hashmap.get("green")); // '#68bt56'
console.log(hashmap.get("blue")); // undefined
console.log(hashmap.get("pink")); // '#765678'
console.log(hashmap.get("cyan")); // '#678765'

// return all the keys in the hashmap
keys(){
  let keys =[];
  for(let i=0;i<this.keyValues.length;i++){
    if(this.keyValues[i]){
      for(let j=0;j<this.keyValues[i].length;j++){
        keys.push(this.keyValues[i][j][0]);
      }
    }
  }
  return keys;
}
// return all the unique values in the hashmap
values(){
  let values =[];
  for(let i=0;i<this.keyValues.length;i++){
    if(this.keyValues[i]){
      for(let j=0;j<this.keyValues[i].length;j++){
        if(!values.includes(this.keyValues[i][j][1])){
          values.push(this.keyValues[i][j][1]);
        }
      }
    }
  }
  return values;
}

// [ 'green', 'pink', 'cyan', 'orange', 'maroon', 'red' ]
// [ '#68bt56', '#765678', '#678765', '#tndu74', '#878787' ]

BigO of hash maps

• Insertion, Deletion, Access in best and average case is O(1)
• In worst case(a hash function that maps every key to the same hash) Insertion, Deletion, Access takes O(n)

---

Graphs

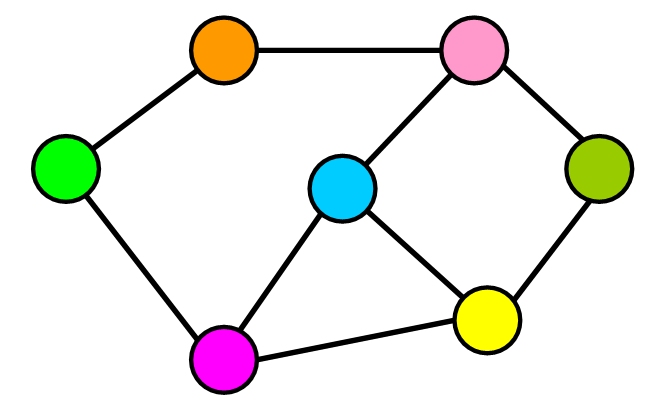
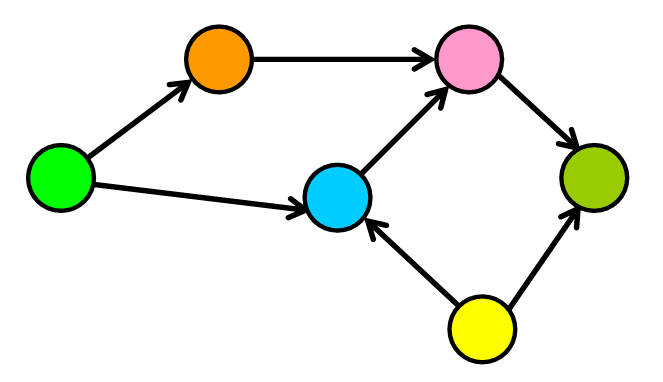
A Graph consists of a finite set of vertices(or nodes) and set of Edges which connect a pair of nodes.
They are used to represent elements that share connections

• A Tree is a special type of a graph, in which any two vertices are connected by exactly one path
• In graphs there is no root or parent node or starting point, all nodes are equal

Graphs are highly used in

• Social Networks
• Location/Mapping
• Recommendation Engines
• Internet
• Web pages linking to other pages
• Visual Hierarchy
• Routing Algorithms
• EVERYWHERE

Types of Graphs

• Undirected Graphs
  Edges do not have a specific direction.You can go from one node to another and return through that same path
  Example - Facebook friends graph
  

• Directed Graphs
  In directed graphs, edges have a direction. They go from one node to another, and there is no way to return to the initial node through that edge
  Example - Instagram followers graph
  

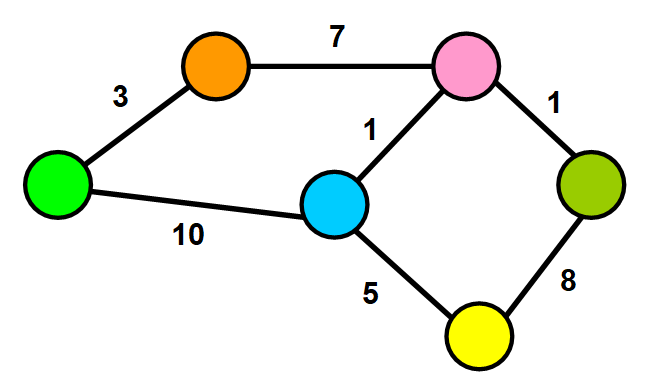
• Weighed Graphs In weighted graphs, each edge has a value associated with it called weight.
  Weights could represent distance, time, the number of connections shared between two users in a social network
  Example - Google Maps are weighted with distance
  

• Cycles in a graph
  

Store graphs

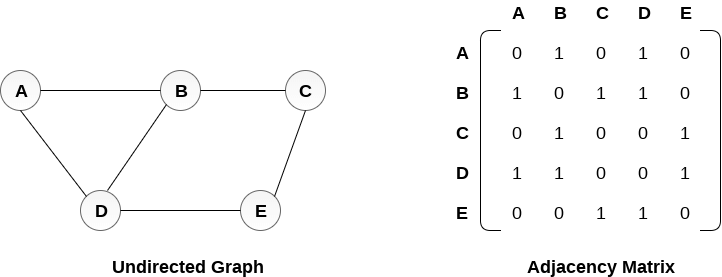
• Matrix is a 2 dimensional structure mostly implemented using nested arrays

• Adjecency Matrix - Connections can be represented by Boolean values in adjacency matrix
  

• Adjecency List - store all connections of a node n at the nth value in array
  For strings use hash tables
  

Adjecency Matrix vs Adjecency List

• Adjecency List can take up less space (in sparce graphs) while Adjecency Matrix takes more space
• In Adjecency List its faster to iterate over all edges as compared to Adjecency Matrix
  In Adjecency Matrix we store values that have 0 ie no edge, while in Adjecency List we only store edges
• Adjecency List can be slower to lookup for specific edge as compared to Adjecency Matrix
  Querying for edge is O(1) for Adjecency Matrix and O(v + e) for Adjecency List

Implementing Graph using Adjecency List

class Graph {
  constructor() {
    this.list = {};
  }
  addVertex(vertex) {
    if (!this.list[vertex]) this.list[vertex] = [];
  }
  addEdge(vertex1, vertex2) {
    if (!this.list[vertex1] || !this.list[vertex2]) return undefined;
    this.list[vertex1].push(vertex2);
    this.list[vertex2].push(vertex1);
  }
}

const graph = new Graph();
graph.addVertex("Tokyo");
graph.addVertex("Rio");
graph.addVertex("Denver");
graph.addVertex("Hongkong");
console.log(graph);
// Graph { list: { Tokyo: [], Rio: [], Denver: [], Hongkong: [] } }
graph.addEdge("Tokyo", "Rio");
graph.addEdge("Tokyo", "Denver");
graph.addEdge("Hongkong", "Denver");
graph.addEdge("Hongkong", "Rio");
console.log(graph);
// Graph { list: { Tokyo: [ 'Rio', 'Denver' ], Rio: [ 'Tokyo', 'Hongkong' ], Denver: [ 'Tokyo', 'Hongkong' ], Hongkong: [ 'Denver', 'Rio' ] } }

removeEdge(vertex1, vertex2){
  if(!this.list[vertex1] || !this.list[vertex2]) return undefined;
  this.list[vertex1] = this.list[vertex1].filter(v => v !== vertex2);
  this.list[vertex2] = this.list[vertex2].filter(v => v !== vertex1);
}
// remove the vertex and all of its connections and it from all connections
removeVertex(vertex){
  if(!this.list[vertex]) return undefined;
  for(var connection of this.list[vertex]){
    this.removeEdge(vertex, connection);
  }
  delete this.list[vertex];
}

graph.removeEdge('Tokyo', 'Denver');
console.log(graph);
// Graph { list: { Tokyo: [ 'Rio' ], Rio: [ 'Tokyo', 'Hongkong' ], Denver: [ 'Hongkong' ], Hongkong: [ 'Denver', 'Rio' ]}}
graph.removeVertex('Hongkong');
console.log(graph);
// Graph { list: { Tokyo: [ 'Rio' ], Rio: [ 'Tokyo' ], Denver: [] } }

---

Graph Traversal

Graph Traversal - Visiting every vertex in a graph atleast once

Graph Traversal is used in

• Web crawlers
• Finding closest matches/ reccomendation
• peer to peer networking
• GPS navigation
• Solving mazes, AI shortest path to win a game

Traversing a Graph

• Since graphs do not have root or parent nodes or hierarchy DFS and BFS seems confusing
• For a graph that has a node 'A' which is connected to 'B' 'E' and 'P'
• BFS means vistiting 'A' and then all its connections ie 'B' 'E' 'P' in any order, and then visiting their connections
• DFS means vistiting 'A' then visiting one of its connections 'B' and then visiting its connections 'C', before visiting 'E'

Implementing graph traversal

const graph = new Graph();
graph.addVertex("A");
graph.addVertex("B");
graph.addVertex("C");
graph.addVertex("D");
graph.addVertex("E");
graph.addVertex("F");
graph.addEdge("A", "B");
graph.addEdge("A", "C");
graph.addEdge("B", "D");
graph.addEdge("C", "E");
graph.addEdge("D", "E");
graph.addEdge("D", "F");
graph.addEdge("E", "F");
console.log(graph);
// Graph {list: {A: [ 'B', 'C' ],B: [ 'A', 'D' ],C: [ 'A', 'E' ],D: [ 'B', 'E', 'F' ],E: [ 'C', 'D', 'F' ],F: [ 'D', 'E' ]}}
/* 
                                A
                          
                        B             C
                                        
                        D ----------- E
                                        
                                F  

*/

DFS using recursion

// Wrote it myself
dfsRecursive(vertex){
  let visited = [];
  let list = this.list;
  (function traverseRecursievely(vertex){
    visited.push(vertex);
    if(!(list[vertex] && list[vertex].length)) return null;
    for(let connection of list[vertex]){
      if(!visited.includes(connection)){
        traverseRecursievely(connection)
      }
    }
  })(vertex);
  return visited;
}

// [ 'A', 'B', 'D', 'E', 'C', 'F' ]
// used closure, can be done using simple function defination too
// instead of using includes, maintain a hash

DFS Iteratievely / Using our own Stack instead of using call stack

dfsIteratievely(vertex){
  if(!vertex || !this.list[vertex]) return false;
  let result = [];
  let visited = {};
  let stack = [];
  stack.push(vertex);
  while(stack.length){
    const node = stack.pop();
    result.push(node);
    if(!visited[node]) visited[node] = true;
    for(let connection of this.list[node]){
      if(!visited[connection]) {
        visited[connection] = true;
        stack.push(connection);
      }
    }
  }
  return result;
}

// [ 'A', 'C', 'E', 'F', 'D', 'B' ]
// writing own stack instead of using call stack

BFS

bfs(vertex){
  if(!vertex || !this.list[vertex]) return false;
  let result = [];
  let visited = {};
  let queue = [];
  queue.push(vertex);
  while(queue.length){
    const node = queue.shift();
    result.push(node);
    if(!visited[node]) visited[node] = true;
    for(let connection of this.list[node]){
      if(!visited[connection]){
        visited[connection] = true;
        queue.push(connection);
      }
    }
  }
  return result;
}

// [ 'A', 'B', 'C', 'D', 'E', 'F' ]
// Using a queue instead of a stack

---

Dijkstras Algorithm (Shortest Path algorithm)

Finds the shortest path between two vertices/nodes on a graph

• Most famous and widely used algorithms around

Algorithm

Find the shortest path from A to E

1. Every time we look to visit a new node, we pick the node with the smallest know distance to visit first
2. Once we have moved to that node, we look at each of its neighbour
3. For each neighbouring node, we calculate distance by summing the total edges that led to the node we are checking from starting node
4. If the new total distance to a node is less then the previous total, we store the new shorter distace for that node

The Approch of Dijkstras Algorithm

1. Create a weighted graph and add vertices, edges and weights

   {
     "list": {
       "A": [{"vertex": "B","weight": 4},{"vertex": "C","weight": 2}],
       "B": [{"vertex": "A","weight": 4},{"vertex": "E","weight": 3}],
       "C": [{"vertex": "A","weight": 2},{"vertex": "D","weight": 2},{"vertex": "F","weight": 4}],
       "D": [{"vertex": "C","weight": 2},{"vertex": "F","weight": 1},{"vertex": "E","weight": 3}],
       "E": [{"vertex": "B","weight": 3},{"vertex": "D","weight": 3},{"vertex": "F","weight": 1}],
       "F": [{"vertex": "C","weight": 4},{"vertex": "D","weight": 1},{"vertex": "E","weight": 1}]
     }
   }

2. Create an array 'visited' which will save all visited nodes, initially empty
   visited : []

3. Create a priority queue which has all vertices and their shortest distances from 'A', distances initially '0' for 'A' and 'Infinity' for all other nodes

   [
     { vertex: "A", shortestDist: 0 },
     { vertex: "B", shortestDist: Infinity },
     { vertex: "C", shortestDist: Infinity },
     { vertex: "D", shortestDist: Infinity },
     { vertex: "E", shortestDist: Infinity },
     { vertex: "F", shortestDist: Infinity },
   ];

4. Create a hash called 'previous' which will store where did we come from to reach a node, eg - F can be reached from D, initially will be null
   { A : null, B : null, C : null, D : null, E : null, F : null }

5. Select the node with the lowest priority/shortest distances from the priority queue, ie 'A' and Look at each of its neighbours

6. First neighbour is 'B', look at the shortestDist for B which is Infinity
   now we reached B from A and the distance was 4 which is less then Infinity, so we update the priority queue as 4 is the shortest distance to get to B
   {vertex:'B', shortestDist: 4}
   since we reached B from A we update previous as
   { A : null, B : 'A', C : null, D : null, E : null, F : null }

7. Simillarly for C
   {vertex:'C', shortestDist: 2}
{ A : null, B : 'A', C : 'A', D : null, E : null, F : null }

8. Since all neighbours of A are done, and add it to visited
   visited : ['A']

9. Repeat by picking the lowest priority/shortest distance from priority queue, ie C and Look at each of its neighbours, ie D and F

   [
     { vertex: "A", shortestDist: 0 },
     { vertex: "B", shortestDist: 4 },
     { vertex: "C", shortestDist: 2 },
     { vertex: "D", shortestDist: Infinity },
     { vertex: "E", shortestDist: Infinity },
     { vertex: "F", shortestDist: Infinity },
   ];

10. After visiting D and F the state will be like

    [
      { vertex: "A", shortestDist: 0 },
      { vertex: "B", shortestDist: 4 },
      { vertex: "C", shortestDist: 2 },
      { vertex: "D", shortestDist: 4 },
      { vertex: "E", shortestDist: Infinity },
      { vertex: "F", shortestDist: 6 },
    ];

    { A : null, B : 'A', C : 'A', D : 'C', E : null, F : 'C' }
visited : ['A', 'C']

11. Repeat for all nodes that are not in visited based on shortestDist in priority queue

12. At the End the values will be

    [
      { vertex: "A", shortestDist: 0 },
      { vertex: "B", shortestDist: 4 },
      { vertex: "C", shortestDist: 2 },
      { vertex: "D", shortestDist: 4 },
      { vertex: "E", shortestDist: 6 },
      { vertex: "F", shortestDist: 5 },
    ];

    { A : null, B : 'A', C : 'A', D : 'C', E : 'F', F : 'D' }
visited : ['A', 'C', 'B', 'D']

13. So the shortest distance from A to E will be as
    { A : null, B : 'A', C : 'A', D : 'C', E : 'F', F : 'D' }
    E --> F --> D --> C --> A
    ie A -> C -> D -> F -> E distance is 6

    ---

Implementation

Implementing a weighted graph

class WeighedGraph {
  constructor() {
    this.list = {};
  }
  addVertex(vertex) {
    if (!this.list[vertex]) this.list[vertex] = [];
  }
  addEdge(vertex1, vertex2, weight) {
    if (!this.list[vertex1] || !this.list[vertex2]) return undefined;
    this.list[vertex1].push({ vertex: vertex2, weight });
    this.list[vertex2].push({ vertex: vertex1, weight });
  }
}

const graph = new WeighedGraph();
graph.addVertex("A");
graph.addVertex("B");
graph.addVertex("C");
graph.addVertex("D");
graph.addVertex("E");
graph.addVertex("F");
graph.addEdge("A", "B", 4);
graph.addEdge("A", "C", 2);
graph.addEdge("B", "E", 3);
graph.addEdge("C", "D", 2);
graph.addEdge("C", "F", 4);
graph.addEdge("D", "F", 1);
graph.addEdge("D", "E", 3);
graph.addEdge("E", "F", 1);

/* 
{
  "list": {
    "A": [{"vertex": "B","weight": 4},{"vertex": "C","weight": 2}],
    "B": [{"vertex": "A","weight": 4},{"vertex": "E","weight": 3}],
    "C": [{"vertex": "A","weight": 2},{"vertex": "D","weight": 2},{"vertex": "F","weight": 4}],
    "D": [{"vertex": "C","weight": 2},{"vertex": "F","weight": 1},{"vertex": "E","weight": 3}],
    "E": [{"vertex": "B","weight": 3},{"vertex": "D","weight": 3},{"vertex": "F","weight": 1}],
    "F": [{"vertex": "C","weight": 4},{"vertex": "D","weight": 1},{"vertex": "E","weight": 1}]
  }
}
*/

Implementing a simple priority queue

class PriorityQueue {
  constructor() {
    this.values = [];
  }
  enqueue(vertex, shortestDist) {
    this.values.push({ vertex, shortestDist });
    this.values.sort((a, b) => a.shortestDist - b.shortestDist);
  }
  dequeue() {
    return this.values.shift();
  }
}

Implementing Dijkstra

dijkstra(start, finish){
  let visited = [];
  const queue = new PriorityQueue();
  const distances = {};
  const previous = {};
  let smallest;
  let path = [];
  for(let node in this.list){
    if(node === start){
      distances[node] = 0;
      queue.enqueue(node, 0);
    }else{
      distances[node] = Infinity;
      queue.enqueue(node, Infinity);
    }
    previous[node] = null;
  }
  while(queue.values.length){
    // select the node with the shortest distances from the priority queue
    smallest = queue.dequeue().vertex;
    // if its the end node we are done
    if(smallest === finish){
      while(previous[smallest]){
        path.push(smallest);
        smallest = previous[smallest];
      }
      path.push(smallest);
      return path.reverse();
    }
    // look at each of its neighbours
    for(let connection of this.list[smallest]){
      // if not visited and if newDist is less then update everywhere
      if(!visited.includes(connection.vertex)){
        let initialDistance = distances[connection.vertex];
        let newDist = connection.weight + distances[smallest];
        if(newDist < initialDistance){
          distances[connection.vertex] = newDist;
          queue.enqueue(connection.vertex, newDist);
          previous[connection.vertex] = smallest;
        }
      }
    }
    // since all neighbours of are done, and add it to visited
    visited.push(smallest);
  }
}

console.log(graph.dijkstra('A','E')); // [ 'A', 'C', 'D', 'F', 'E' ]
console.log(graph.dijkstra('A','B')); // [ 'A', 'B' ]
console.log(graph.dijkstra('A','F')); // [ 'A', 'C', 'D', 'F' ]
console.log(graph.dijkstra('B','C')); // [ 'B', 'A', 'C' ]
console.log(graph.dijkstra('B','F')); // [ 'B', 'E', 'F' ]

---

Optimization problem

Optimization problem is the problem of finding the best solution from all feasible solutions

Optimization problem is the problem that demands Minimum results or Maximum results

There are 3 approaches to solve Optimization problems

1. Greedy Method
2. Dynamic Programming
3. Branch and Bound

---

Dynamic Programming

Method of solving a complex problem by breaking it down into a collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions

Indicators on when to use Dynamic Programming - Overlapping Subproblems and Optimal Substructure

• Most problems cant solved by dynamic programming, but for the few that can be solved it makes a very huge difference in performance

Overlapping Subproblems

A problem is said to have overlapping subproblems if it can be broken down into sub problems which are reused several times

• Eg of overlapping subproblems - Fibonacci Sequence
  
• To find fibonacci(5) we add fibonacci(4) + fibonacci(3) , We calculate fibonacci(3) twice
• Merge Sort is not an example of overlapping subproblems, We do the same process recursievely but the values are different everytime
• mergeSort([10,70,30,15]) -> mergeSort([10,70]) and mergeSort([30,15]) -> mergeSort([10]) and mergeSort([70]) and mergeSort([30]) and mergeSort([15])
• storing the solution of mergeSort([30]) or any other smaller part, will have no use

Optimal Substructure

A problem is said to have optimal substructure if an optimal solution can be constructed from optimal solutions of its sub problems

• Eg - Fibonacci Sequence
• The optimal solution for fibonacci(5) can be constructed from optimal solution for fibonacci(4) and fibonacci(3)
• Eg - Shortest Path on a graph
• For a seq A -> B -> C -> D -> E, the best way to E can be constructed from the best way to D
• Longest Simple Path is not an example of optimal substructure (simple means no repeating)
• Longest path from A to C = A -> B -> C and C to D = C -> B -> D
• A to D not equal to A -> B -> C -> B -> D, ( A to D != A to C + C to D )
• Finding cheapest flight from SanFrancisco to Alaska, looks like a optimal substructure but is not
• The cheapest flight from SanFrancisco to Alaska is as SanFrancisco -> Seatle -> Alaska
• So the cheapest flight from SanFrancisco to Seatle, should have been SanFrancisco -> Seatle but its not, its SanFrancisco -> Portland -> Seatle
• So the cheapest flight from SanFrancisco to Alaska should be SanFrancisco -> Portland -> Seatle -> Alaska, but its not the case, there are various other parameters

Solving without Dynamic Programming (Recursievely)

• Since Fibonacci Sequence has both overlapping subproblems and optimal substructure we can solve it using dynamic programming

  function fib(n) {
    if (n <= 2) return 1;
    return fib(n - 1) + fib(n - 2);
  }

• Recursive solution has a time complexity of O(2 ^ n) which is Terrible
• For calculating fib(7), fib(5) is calculated twice fib(4) 3 times and fib(3) 5 times
• Calculating fib(45) takes upto 10 sec and fib(over 100) takes way too long and call stack is exceded

Refactoring using Dynamic Programming

• Using Memoization

  Memoization - Storing the results in memo and passing it to every call

  function memoizedFib(n, memo = []) {
    console.log(memo);
    if (n <= 2) return 1;
    if (memo[n]) return memo[n];
    var result = memoizedFib(n - 1, memo) + memoizedFib(n - 2, memo);
    memo[n] = result;
    return result;
  }

• We storing the results in memo and passing it to every call

• Memo for n=10 is [ <3 empty items>, 2, 3, 5, 8, 13, 21, 34 ]

• Memoization solution has a time complexity of O(n) which is a lot better

• For calculating fib(7), everything is calculated just once
  

Tabulation - A Bottom-up Approach, Storing the result of a previous result in a table (usually an array), Usually done using iteration

• Tabulation - Storing the result of a previous result in a table (usually an array)

• Usually done using iteration

• Better Space Complexity can be achived using Tabulation

  function tabulatedFib(n) {
    if (n <= 2) return 1;
    var fibNums = [0, 1, 1];
    for (var i = 3; i <= n; i++) {
      fibNums[i] = fibNums[i - 1] + fibNums[i - 2];
    }
    return fibNums[n];
  }

• Tabulated solution has a time complexity of O(n) which is same as memoized solution

• Tabulated approch is a lot better then memoized as even the memoized would exceed call stack above fib(100000)

• Tablulated version return Infinity for fib(100000) which is math and roundoff, doesnt break though

Leetcode problems

• Climb stairs
• Target sum
• Grid traversal

---

Backtracking

• Backtracking is an algorithmic technique that considers searching in every possible combination for solving a computational problem.
• It is known for solving problems recursively one step at a time and removing those solutions that that do not satisfy the problem constraints at any point of time.
• It is a refined brute force approach that tries out all the possible solutions and chooses the best possible ones out of them.

If the current solution is not suitable, then eliminate that and backtrack (go back) and check for other solutions.

Backtracking is not for optimization problems (best path, max or min), Backtracking is when you have multiple solutions and you want all of those solutions

Backtracking uses DFS

Snippet from Binary watch leetcode problem

/* 
Since this is a backtracking problem, lets think of how backtracking works
Consider we have a starting point S, and 3 ways to go A B C, from A we can go to A1 A2 A3, and similarly from B C as well
Suppose our goal is at C2, how we would go by backtracking would be
S-A-A1, S-A-A2, S-A-A3, S-B-B1, S-B-B2, S-B-B3, S-C-C1, S-C-C2-Goal
This is exactly how DFS traversal would go
We implement DFS using stack, or recursion (call-stack)
*/

Example of Permutations Combinations

Consider we have 3 students (boy1, boy2, girl1) and 3 seats
How many ways can we arrange them in : 3 x 2 x 1 ie 3! = 6 ways
We want to print all of those arrangements
To do that lets visualize solutions as a tree

                             s

          b1                 b2                  g1
    b2         g1      b1        g1        b1         b2

    g1         b2      g1        b1        b2         b1

Each leaf to root path represnts one of the 6 solutions
Backtracking problems usually have constrains, so lets impose one here, girl should not sit in middle This condition is called as bounding function

                             s

          b1                 b2                  g1
    b2         g1      b1        g1        b1         b2

    g1                 g1                  b2         b1

After applying constrain we have 4 solutions instead of 6

Backtracking usecases

• N-Queens Problem - The N-Queens problem is a classic chessboard problem. Given an N×N chessboard, the task is to place N queens in such a way that no two queens threaten each other. In other words, no two queens should share the same row, column, or diagonal.
  For N=8, a solution involves placing 8 queens on the chessboard in such a way that no two queens attack each other.
• Sudoku is a number-placement puzzle. The objective is to fill a 9×9 grid with digits from 1 to 9 in such a way that each row, each column, and each of the nine 3×3 subgrids that compose the grid contain all of the digits from 1 to 9 without repetition.
• Permutations - The task is to generate all possible arrangements of a set of elements. In the context of permutations, the order of elements matters.
  For a set {1, 2, 3}, the permutations would be {1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 1, 2}, {3, 2, 1}.

My take:
If in a problem we need to calculate all possible permutations and combinations, it can be done using backtracking

Backtracking Pseudocode

function isValidState(state) {
  // Check if it is a valid solution
  return true;
}

function getCandidates(state) {
  // Return an array of candidates for the current state
  return [];
}

function search(state, solutions) {
  if (isValidState(state)) {
    solutions.push([...state]); // Make a copy of the state
    // return; // Uncomment this line if you want to stop after finding the first solution
  }

  for (const candidate of getCandidates(state)) {
    state.push(candidate);
    search(state, solutions);
    state.pop();
  }
}

function solve() {
  const solutions = [];
  const state = [];
  search(state, solutions);
  return solutions;
}

const result = solve();

Leetcode problems

• Word search
• Binary Watch

---

Greedy Algorithm

Greedy Method is used for solving optimization problems

A greedy algorithm is a simple, intuitive algorithm that is used in optimization problems. The algorithm makes the optimal choice at each step as it attempts to find the overall optimal way to solve the entire problem. However, in many problems, a greedy strategy does not produce an optimal solution.

In What case would greedy algorithm fail ie not produce an optimal solution?
Consider a tree

                        3
                   4        7
                 6   20   9   11

In this case greedy algorithm chooses - 3 -> 7 -> 11 = 21 instead of 3 -> 4 -> 20 = 37
as at step 1 among 4 and 7, 7 is the optimal choice and among 9 and 11, 11 is

Greedy Algorithm never reconsiders its choices

When to use greedy method ?
Problems on which greedy approach works has 2 properties

1. Should be an Optimization problem (Min or Max is demanded)
2. Greedy choice property - global optimum can be arrived by choosing local optimum
3. Optimal Substructure (Simillary to DP) -

This is a difference between dp and greedy algorithm -
DP is exhaustive and is guaranteed to find a solution,
greedy method fails in some cases and never reconsiders its choices

Greddy algorithm usecases

• Coin Change Problem - Given a set of coins with different denominations and a total amount of money, find the minimum number of coins needed to make up that amount.
  If the coins are [1, 2, 5] and the amount is 11, the answer is 3 (two 5-coins and one 1-coin).

• Huffman Coding - Huffman coding is a compression algorithm that assigns variable-length codes to input characters based on their frequencies. It ensures that more frequent characters have shorter codes.
  For a given set of characters and their frequencies, the algorithm constructs a binary tree where shorter codes represent more frequent characters.

• Scheduling - Scheduling involves arranging tasks or jobs to be executed over time, subject to certain constraints or objectives. This can include minimizing completion time, maximizing resource utilization, etc.
  In job scheduling, tasks with different processing times need to be scheduled on machines to minimize the total completion time.

My take:
Use greedy algorithm for problems of the kinds where we first fill the jar with stones, then pebbles, and then sand
Eg Maximum units on a truck, where we select max unit boxes first, then second max unit box, then third and so on
Maximum icecream bars, where we select icecreams with least cost first, then the second least cost and so on

Leetcode problems

• Maximum units on a truck
• Maximum icecream bars

---

DP vs Greedy algorithm vs Backtracking

Dynamic Programming:

• Idea: Dynamic programming is a method for solving problems by breaking them down into smaller subproblems and solving each subproblem only once, storing the solutions to subproblems to avoid redundant work.
• Approach: It involves solving subproblems and building up a solution incrementally. It uses memoization (storing intermediate results) or tabulation (building a table) to avoid recomputing the same subproblems.
• Use Cases: Dynamic programming is suitable for problems with overlapping subproblems and optimal substructure. Classic examples include the knapsack problem, longest common subsequence, and shortest path problems.

Greedy Algorithm:

• Idea: Greedy algorithms make locally optimal choices at each stage with the hope of finding a global optimum.
• Approach: At each step, it selects the best available option without considering the future consequences. It doesn't reconsider previous choices.
• Use Cases: Greedy algorithms are suitable for problems where a locally optimal choice also leads to a globally optimal solution. Examples include coin change problem, Huffman coding, and scheduling.

Backtracking:

• Idea: Backtracking is a trial-and-error-based algorithmic paradigm used to solve optimization problems. It explores all possible solutions by trying different choices and backtracks when a choice leads to an infeasible solution.
• Approach: It systematically explores the solution space by making choices, and if a choice leads to a dead-end, it backtracks and tries a different choice. It is often implemented using recursion.
• Use Cases: Backtracking is useful when there are multiple solutions to a problem, and it's necessary to find all solutions. Examples include the N-Queens problem, Sudoku, and generating all permutations.