Peekaby Name Block Solution

피카비 이름 블록 문제에 대한 풀이 입니다.

How to Run

$ pip install -r requirements.txt
$ python solution.py

위 코드를 실행하면 output.txt가 생성 됩니다.

About the Files

• input.txt: 입력 파일로서 아이들의 한글 이름에 대한 로마자 표기 정보가 담겨 있습니다.
• solution.py: 문제를 해결하기 위한 소스 코드가 담겨 있습니다.
• output.txt: 출력 파일로서 solution.py를 실행하면 생성 됩니다.

솔루션에 대한 자세한 설명

이름 블록이란?

하나의 이름 블록 세트에는 정해진 갯수의 블록이 있고, 이 블록에는 각 면에 알파벳이 쓰여져 있습니다. 부모는 이 블록들을 조합하여 아이의 영문 철자 이름을 만들 수 있습니다. 사업 개발팀에서 이러한 이름 블록을 기획 하였습니다.

블록을 디자인 하고 공장에 발주를 해야 하는데, 다음과 같은 요구 조건들이 있었습니다.

• 주문하는 블록의 종류를 최소화 하고 싶다.
• 블록 종류별로 소진 시기를 비슷하게 맞추고 싶다.
• 행사 때 사용 할 예정이고, 미리 아이의 이름을 받아서 블록을 조합하여 제공 할 수 있다.

이러한 요구 조건들을 만족 하기 위해서는 어떤 블록을 어떤 비율로 주문 해야 할까요?

이 문제를 풀기 위해서는 일단 블록으로 표현 해야 하는 이름들이 무엇인지 알아야 하고, 블록의 종류가 몇 개가 되어야 하고 각 블록에 어떤 알파벳이 들어가야 하는지, 그리고 각 블록을 어떤 비율로 발주 해야 하는지 알아야 합니다.

영문 아이 이름 데이터셋

블록으로 어떤 이름을 만들어야 하는지 알기 위해서 영문 아이 이름 데이터셋을 만들었습니다. 2021년부터 2023년까지 각 년도별로 상위 2000개의 이름들을 수집 했습니다. 그리고 중복된 이름들을 합치니 총 2078개의 이름을 수집 할 수 있었습니다. 수집한 이름을 해당 기간 출생아 수와 비교해 보니, 약 78.4%의 아이들이 수집한 이름 중에 있다고 추정 할 수 있었습니다.

영문 이름을 얻기위해서 네이버 이름 변환기를 사용했습니다. 네이버 이름 변환기는 많이 주로 많이 쓰이는 한글 로마자 표기법을 사용해서 영문 이름을 만들어 줍니다. 이를 사용해서 2078개의 이름을 영문 이름으로 변환 했습니다.

이름 블록 문제

이름 블록 문제는 다음과 같이 정의 합니다.

피카비 행사에 사용할 이름 블록에는 각 면에는 알파벳 혹은 로고가 쓰여져 있습니다. 행사 전에 미리 아이의 이름을 받아서 아이의 이름을 만들 수 있는 블록들을 조합 하여 행사때 선물로 증정 하려고 합니다. 이름 블록을 공장에 발주를 해야 하는데 피카비는 발주하는 이름 블록의 종류를 최소화 하고, 각 종류의 블록이 비슷한 속도로 소진되게 하고 싶습니다. 이를 위해서는 어떤 알파벳이 쓰여져 있는 블록들을 디자인 해야 하고, 각 블록을 어떤 비율로 발주 해야 할까요?

이 문제를 풀기 위해서는 아래 개념들을 알아야 합니다.

• constraint programming (CP): 제약 조건을 만족하는 해를 찾는 문제를 푸는 방법
• satisfiability problem (SAT): 특정 논리식을 만족하는 해를 찾는 문제
• constraint satisfaction problem: 수학적으로 특정 상태를 만족해야 하는 문제

여기서는 constraint satisfaction problem이 중요하기 때문에 이에 대하여 자세히 알아보겠습니다. 참고로 constraint satisfaction problem은 constraint programming과 satisfiability problem의 교집합이라고 보시면 됩니다.

이런 저런 복잡한 개념 말고, 모든 경우의 수를 테스트 해 보는 방법을 사용하면 되지 않을까 생각 하실 수 있습니다. 모든 알파벳을 블록에 쓸 수 있는 모든 경우의 수에 대해서 모든 이름을 표현 할 수 있는지 테스트를 해 보면 되지 않을까요? 이 방법은 쉽고 간단 하지만 (이러한 방법을 brute force 라고 합니다.) 경우의 수가 지나치게 많아서 현실적으로 불가능 합니다. 예를 들어, 8개의 블록이 있고 각 블록에 6개의 알파벳을 쓸 수 있다고 해봅시다. 알파벳이 총 26개가 있기 때문에 모든 경우의 수는 ${26 \choose 6}^8 = 7.9 \times 10^{42}$ 입니다 (하나의 알파벳이 여러 주사위에 쓰여질 수 있습니다.). 하나의 경우에 대해서 테스트 하는데 1 밀리초가 걸린다고 해도 약 $2 \times 10^{36}$ 일이 걸립니다. 즉, 다 계산하는데 몇 백 억년의 몇 백배가 넘게 걸립니다.

constraint satisfaction problem (CSP)

CSP의 예시들은 다음과 같습니다.

• 색칠하기: 지도에 있는 각 지역에 색을 칠하되 인접한 지역은 같은 색으로 칠하지 않는 문제
• 스도쿠: 9x9 크기의 격자에 1부터 9까지의 숫자를 채우되, 각 행과 각 열, 그리고 3x3 크기의 격자에 같은 숫자가 중복되지 않도록 채우는 문제
• 스케줄링: 각 작업의 시작 시간과 종료 시간이 주어졌을 때, 모든 작업이 겹치지 않도록 스케줄을 짜는 문제

위 예시들 중에는 스도쿠가 제일 이름 블록 문제와 비슷 합니다.

알고리즘에서 문제를 푸는 알고리즘을 처음부터 설계하는 것도 중요하지만, 내가 풀려는 문제와 이미 잘 알려진 문제들 중에 어떤 문제와 같은지 찾는 것도 중요 합니다.

툴: Google OR-Tools

Google OR-Tools는 Google에서 만든 최적화 문제를 푸는 라이브러리 입니다. Python, C++, Java, C# 등에서 사용할 수 있습니다. 이 라이브러리를 사용하여 이름 블록 문제를 풀어 보겠습니다.

OR-Tools는 변수들을 정의하고, 각 변수들간의 제약 사항 (constraint)를 정의 합니다. 그리고 이를 문제 해결 엔진 (solver)에 넘겨주면, 문제를 풀어 줍니다. 그래서 가장 중요한 것은 이름 블록 문제를 어떻게 문제 해결 엔진이 풀 수 있는 형태로 바꿔주는지 입니다. 즉, 문제를 OR-Tools를 통해서 정의 하는 것이 곧 이 문제를 푸는 것 입니다.

문제 정의

이름 블록 문제를 OR-Tools를 통해서 정의 해 보겠습니다. 문제를 정의하기 위해서는 문제를 풀기 위한 변수들을 정의해야 합니다. 이 문제에서는 다음과 같은 변수들이 있습니다.

• 이름-블록 매핑: 이름을 이름 블록으로 표현 할 때 각 철자를 몇 번째 블록으로 표현할지를 나타내는 변수
• 블록 디자인: 블록 타입별로 어떤 알파벳이 쓰여져 있는지를 나타내는 변수
• 블록 갯수: 블록 타입별로 몇 개의 블록이 필요한지를 나타내는 변수
• 블록 사용 여부: 블록의 갯수가 1 이상인지를 나타내는 변수 (왜 필요한지는 뒤에서 설명 합니다.)

위에 조건에 보면 한 명에 고객에게 전달하는 블록의 세트는 고정되지 않아도 됩니다. 다만, 각 블록 타입이 비슷한 속도로 소진되게 하고 싶다는 조건이 있습니다. 그래서 블록 세트가 고정 되어야 한다고 가정하고 문제를 풀도록 하겠습니다. 그러면 블록 세트에 들어가는 블록의 갯수에 비례해서 발주를 하면 됩니다.

변수는 아니지만 문제를 풀기 위해 필요한 것들도 있습니다.

• 이름 세트: n 개의 이름이 있는 이름 세트. 이 문제의 입력 값이라 생각 하면 됩니다.

좀 더 수학적으로 표현 해 보겠습니다.

이름 세트

이름 세트 $N$은 $n \times l$ 의 행렬로서 $l$은 이름 세트에 있는 이름들 중 가장 긴 이름의 길이 입니다. $N$의 각 행은 하나의 이름을 나타내며, 각 열은 이름의 각 문자를 나타냅니다. 수학적으로 표현 하면 $N$ 의 $i$ 번째 행의 $j$ 번째 열의 값이 $a$ 라는 것의 의미는 ($N_{i,j}=a$) $N$의 $i$ 번째 이름의 $j$ 번째 문자가 $a$ 번째 알파벳 이라는 라는 것 입니다. 예를 들어, $N$의 2 번째 행의 7 번째 열의 값이 3 이라는 것은 전체 이름중에 2 번째 이름의 7 번째 문자가 3 번째 알파벳인 C라는 것 입니다.

이 문제에서 저희는 기존의 총 26개의 알파벳에 와일드카드 문자를 추가 하여 총 27개의 알파벳을 사용 합니다. 와일드카드 문자는 어떤 알파벳이 와도 상관 없다는 의미 입니다. 와일드카드 위치에는 이미지가 들어갈 수도 있습니다. 와일드카드 문자는 *으로 표현 하며 Z 뒤에 옵니다.

블록 디자인

블록 디자인 $B$는 $27 \times k$ 의 행렬로서 $B$는 특정 알파벳이 특정 블록에 있는지 없는지를 나타냅니다. 각 행은 특정 알파벳을 의미 하고, 각 열은 하나의 블록을 의미 합니다. 만약 행렬의 한 칸의 값이 1이면 해당 행의 알파벳이 해당 열의 블록에 있다는 의미 입니다. 수학적으로 표현 하면 $B$ 의 $i$ 번째 행의 $j$ 번째 열의 값이 $1$ 이라는 것의 의미는 ($B_{i,j}=1$) $B$의 $i$ 번째 알파벳이 $j$ 번째 블록에 있다는 것 입니다. 예를 들어, $B$의 $3$ 번째 행의 $5$ 번째 열의 값이 1 이라는 것은 C 알파벳이 5 번째 블록에 있다는 것 입니다. 값이 0인 경우는 해당 알파벳이 해당 블록에 없다는 것을 의미 합니다.

이름-블록 매핑

이름-블록 매핑은 사실 입력에 대한 답이라고 생각 하면 됩니다. 이름-블록 매핑 $P$는 $n \times l$ 의 행렬로서 $P$의 각 행은 하나의 이름을 나타내며, 각 열은 이름의 각 문자를 나타냅니다. 수학적으로 표현 하면 $P$ 의 $i$ 번째 행의 $j$ 번째 열의 값이 $a$ 라는 것의 의미는 ($P_{i,j}=k$) $N$의 $i$ 번째 이름의 $j$ 번째 문자를 $k$ 번째 블록으로 표현 한다는 것 입니다. 예를 들어, $P$의 2 번째 행의 7 번째 열의 값이 3 이라는 것은 전체 이름중에 2 번째 이름의 7 번째 문자를 3 번째 블록으로 표현 한다는 것 입니다.

블록 갯수

블록 갯수 $C$는 $k$ 크기의 벡터 입니다. $C$의 $i$ 번째 값이 $a$ 라는 것의 의미는 ($C_{i}=a$) $i$ 번째 블록의 갯수가 $a$ 개라는 것 입니다. 예를 들어, $C$의 3 번째 값이 5 라는 것은 3 번째 블록이 5 개라는 것 입니다.

블록 사용 여부

블록 사용 여부 $U$는 $k$ 크기의 벡터 입니다. $U_{i}$는 1 또는 0이 될 수 있으며, $U$의 $i$ 번째 값이 $1$ 라는 것의 의미는 ($U_{i}=1$) $i$ 번째 블록이 사용되었다는 것 입니다. 예를 들어, $U$의 3 번째 값이 1 이면 3 번째 블록이 사용되었다는 것 입니다.

제약 조건 및 최적화 조건

이제 위 변수들이 어떤 조건을 만족 해야 하는지 정의 합니다. 이 문제에서는 다음과 같은 제약 조건이 있습니다.

제약 조건 1: 이름에 속한 특정 알파벳에 특정 블록이 매핑 된다면, 해당 블록에는 해당 알파벳이 있어야 합니다.

이는 $P$ 와 $B$의 관계를 나타내는 제약 조건 입니다. 생각 해 보면 당연한데요 위 문장을 예시로 설명하면 다음과 같습니다. 만약 $P_{1,2}=5$, 즉, 1 번째 이름에서 2 번째 글자를 표현 하기 위해서 5 번째 블록을 사용 해야 한다고 해 봅시다. 그러면 5번째 블록에는 1 번째 이름의 2 번째 글자가 있어야 합니다. 이를 수학적으로 표현 하면 다음과 같습니다.

$$ \forall i, j \in \mathbb{N}, \quad P_{i,j} = k \implies B_{N_{i,j},k}=1 $$

제약 조건 2: 어떤 블록의 갯수는 모든 이름에서 해당 블록이 사용되는 횟수보다 크거나 같아야 합니다.

이는 $P$ 와 $C$의 관계를 나타내는 제약 조건 입니다. 만약 $P_{1,1}=5$, $P_{1,2}=5$, $P_{1,3}=5$ 이라고 해봅시다. 즉, 1 번째 이름에서 5 번째 블록을 3 번 사용 해야 하는 것 입니다. 그러면 5번째 블록은 3개 이거나 이보다 많아야 합니다. 이를 수학적으로 표현 하면 다음과 같습니다.

$$ \forall i \in \mathbb{N}, \quad C_{k} \geq \sum_{j=1}^{l} [P_{i,j} = k] $$

$[P_{i,j} = k]$ 는 $P_{i,j} = k$ 가 참이면 1, 거짓이면 0을 의미 합니다. Iversion notation 이라고 합니다.

제약 조건 3: 하나의 블록은 6개의 알파벳을 가져야 합니다.

블록은 총 6면을 가지고 있기 때문에 6개의 알파벳이 있어야 합니다. 수학적으로 표현 하면 다음과 같습니다.

$$ \forall j \in \mathbb{N}, \quad \sum_{i=1}^{27} B_{i,j} = 6 $$

제약 조건 4: 블록의 사용 여부는 블록의 갯수가 1 이상이면 1, 0 이면 0 입니다.

당연한 이야기 입니다. 수학적으로 표현 하면 다음과 같습니다.

$$ \forall i \in \mathbb{N}, \quad U_{i} = 1 \iff C_{i} \geq 1 $$

최적화 조건 1: 블록의 종류를 최소화 합니다.

블록의 종류는 블록 사용 여부의 총 합과 같습니다. 즉 $U$의 총 합을 최소화 하는 것과 같습니다. 수학적으로 표현 하면 다음과 같습니다.

$$ \min \sum_{i=1}^{k} U_{i} $$

최적화 조건 2: 블록의 종류별 갯수를 비슷하게 하고 불필요한 블록을 추가하지 않습니다.

이 조건은 꼭 필요한 조건은 아닙니다. 다만, 블록별로 발주 단위가 다르면 문제가 될 수도 있기 때문에 이를 최소화 하는 것이 좋습니다.

블록의 종류를 최소화 한다는 것은 가장 많은 블록을 사용하는 블록의 갯수와 0이 아닌 가장 적은 블록을 사용하는 블록의 갯수의 차이를 최소화 한다는 것과 같습니다.

불필요한 블록을 추가하지 않는다는 것은, 블록의 종류별 갯수를 맞추기 위해서 불필요한 종류의 블록의 갯수를 늘리는 것을 방지합니다.

수학적으로 표현 하면 다음과 같습니다.

$$ I = {i \in \mathbb{N} \mid C_{i} \neq 0} $$

$$ \min (\max_{i \in I} C_{i} - \min_{i \in I} C_{i} + \sum_{i=1}^{k} C_{i}) $$

풀기

위에서 정의한 변수와 조건들을 풀어주는 솔버 (solver)를 만들어야 합니다. OR-Tools의 CP-Solver를 사용하면 됩니다. CP-Solver 가 어떻게 동작 하는지는 이 링크에 관련 내용들이 있습니다.

• CPAIOR 2020 Master Class: Constraint Programming
• Search is Dead
• A Peek Inside SAT Solvers - Jon Smock

이 자료들은 배경 지식이 없으면 이해가 잘 안됩니다. 친절하게도 Google에서 N-Queen Problem 예시를 가지고 솔버가 어떤 식으로 동작 하는지 대략 알 수 있게 설명 해 주고 있습니다.

N-Queens Problem 예시

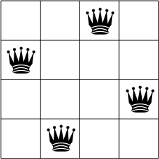
N-Queens Problem은 N x N 크기의 체스판에 N개의 퀸을 놓는 서로 공격 하지 못하게 놓는 문제 입니다.

문제를 푸는 방식은 대략 다음과 같습니다.

1. 가능한 곳에 하나 씩 퀸을 놓습니다.
2. 퀸을 놓을 때마다 퀸이 공격 할 수 있는 곳을 제약 조건으로 추가 합니다.
3. 퀸을 놓을 수 없는 곳에 퀸을 놓으면 다시 1번으로 돌아갑니다.

위에서 2번과 3번을 propagation과 backtracking 이라고 합니다.

• propagation: 솔버가 변수의 값을 정할 때 마다 다른 변수들에 대한 제약 조건을 추가 하는 것 입니다. 예를 들어서 특정 위치에 퀸을 놓으면 좌우와 대각선의 칸 들에는 다른 퀸을 놓을 수 없다는 제약 조건을 추가 합니다.
• backtracking: 솔버가 제약 조건을 추가 하다가 모순이 생기면 이전에 추가한 제약 조건을 제거 하고 다른 값을 시도 하는 것을 말합니다. 예를 들어서 퀸을 잘못 놓아서 더 이상 퀸을 놓을 수 없게 되면, 직전에 놓았던 퀸을 다시 다른 자리로 옮기는 것 입니다.

이름 블록 문제도 비슷합니다. N-Queen 문제에서 체스판 위에 퀸을 놓는 것은 블록들 중 한 면에 어떤 알파벳을 쓰는 것과 같습니다. 블록에 알파벳을 쓸 때마다 제약 조건들을 모두 만족 하는지 보고 만족하지 않으면 다시 다른 알파벳을 써 봅니다.

단계별 최적화

이 문제에는 최적화 해야 하는 것이 두 가지가 있습니다. 하나는 전체 블록의 종류를 최소화 해야 하고 다음으로는 블록 종류별 갯수를 비슷하게 만들어야 합니다. 이 두 목표를 동시에 최적화 하는 것은 어렵기 때문에 따로 최적화를 합니다. 블록의 종류가 적은것이 생산 측면에서 더 중요하기 때문에 블록의 종류부터 최적화를 합니다.

한계점

이 풀이는 이름의 확률 분포를 고려하지 않고 있습니다. 모든 이름이 같은 확률로 등장 함을 가정하고 있고, 이름 데이터 셋 내의 알파벳 분포에 대해서만 고려하고 있습니다.

참고 사항

실제 피카비 이름 블록 제품을 만들 때는 조건을 조금 변형 했었기 때문에 위 솔루션의 결과가 다를 수 있습니다. 대략적인 접근 방법은 같습니다.