Hotspot

Hotspot is a tool for identifying informative genes (and gene modules) in a single-cell dataset.

Importantly 'informative' is decided based on how well a gene's variation agrees with some cell metric - some similarity mapping between cells.

Genes which are informative are those whose expression varies in similar way among cells which are nearby in the given metric.

The choice of metric allows you to evaluate different types of gene modules:

• Spatial: For spatial single-cell datasets, you can define cell similarity by proximity in physical, 2D/3D space. When set up this way, Hotspot can be used to identify spatially-varying genes.
• Lineage: For single-cell datasets with a lineage tracing system, you can infer a cell developmental lineage and use that as the cell metric. Then Hotspot can be used to identify heritable patterns of gene expression.
• Transcriptional: The result of a dimensionality reduction procedure can be used create the similarity metric. With this configuration, Hotspot identifies gene modules with local correlation. This can be particularly useful for interpreting axes of variation in non-linear dimensionality reduction procedures where the mapping between components and genes is not straightforward to evaluate.

Examples

• Spatial Data (Mouse Cerebellum)
• Lineage Data (Mouse Embryogenesis)
• Human CD4 T cells

Other Links

• Publication
• bioRxiv Preprint
  • Associated analysis repo
• Documentation

Installation

Hotspot is installed directly from PyPI using the following command:

pip install hotspotsc

Hotspot can be imported as

import hotspot

Starting with v1.0, Hotspot uses the AnnData data object. If you'd like to use the old version of Hotspot then:

pip install hotspotsc==0.9.1

The old documentation for that version can be found here, but installation will still be pip install hotspotsc==0.9.1.

The old initialization for v0.9.1 has now moved to hotspot.Hotspot.legacy_init, see the docs for usage.

Usage

The following steps are used when analyzing data in Hotspot:

1. Create the Hotspot object
2. Compute the KNN graph
3. Find informative genes (by gene autocorrelation)
4. Evaluate pair-wise gene associations (gene local correlations)
5. Group genes into modules
6. Compute summary per-cell module scores

Here we describe each step in order:

Create the Hotspot object

To start an analysis, first create the hotspot object When creating the object, you need to specify:

• The gene counts matrix
• Which background model of gene expression to use
• The metric space to use to evaluate cell-similarity
• The per-cell scaling factor
  • By default, number of umi per cell is used

For example:

import hotspot
hs = hotspot.Hotspot(
    adata,
    layer_key="counts",
    model='danb',
    latent_obsm_key="X_pca",
    umi_counts_obs_key="total_counts"
)

In the example above:

• adata is a AnnData object of cells by genes
• layer_key is the layer of adata containing count information
• model 'danb' selects the umi-adjusted negative binomial model
• latent_obsm_key is the .obsm key of adata containing Cells x Components matrix (the PCA-reduced space)
• umi_counts_obs_key is the .obs key of adata with the UMI count for each cell

Alternative choices for 'model'

The model is used to fit per-cell expectations for each gene assuming no correlations. This is used as the null model when evaluating autocorrelation and gene-gene local correlations. The choices are:

• danb: 'Depth-adjusted negative binomial' (aka NBDisp model) from M3Drop
• bernoulli: Here only the detection probability for each gene is estimated. Logistic regression on gene bins is used to evaluate this per-gene and per-cell as a function of the cells umi_count value.
• normal: Here expression values are assumed to be normally-distributed and scaled by the values in umi_count.
• none: With this option, the values are assumed to be pre-standardized

Choosing different metrics

Above we used latent_obsm_key as the input option. This assumes that cells are in an N-dimensional space and similarity between cells is evaluated by computing euclidean distances in this space. Either the results of a dimensionality reduction or modeling procedure can be input here, or when working with spatial data, the per-cell coordinates.

Alternately, instead of latent_obsm_key, you can specify either tree or distances_obsp_key.

tree is used for a developmental lineage. In this form, tree should be an ete3.TreeNode object representing the root of a Tree with each cell as its leaves. This could be constructed programmatically (see ete3's documentation for details) or if your lineage is stored in a Newick file format, you can load it into an ete3.TreeNode object by running ete3.Tree('my_newick.txt'). Note: leaf nodes in the tree must have names that match the column labels in the counts input (e.g., cell barcodes).

distances_obsp_key is used to specify cell-cell distances directly. The value entered should be a Cells x Cells matrix in adata.obsp.

Compute the KNN graph

The K-nearest-neighbors graph is computed by running:

hs.create_knn_graph(weighted_graph=False, n_neighbors=30)

Input options:

• weighted_graph: bool, whether or not the graph has weights (scaled by cell-cell distances) or is binary
• n_neighbors: the number of neighbors per cell to use. Larger neighborhood sizes can result in more robust detection of correlations and autocorrelations at a cost of missing more fine-grained, smaller-scale patterns and increasing run-time
• neighborhood_factor: float, used when weighted_graph=True. Weights decay proportionally to exp(-distance^2/distance_N^2) where distance_N is the distance to the n_neighbors/neighborhood_factorth neighbor.

Generally, the above defaults should be fine in most cases.

Find informative genes (by gene autocorrelation)

To compute per-gene autocorrelations, run:

hs_results = hs.compute_autocorrelations()

An optional argument, jobs can be specified to invoke parallel jobs for a speedup on multi-core machines.

The output is a pandas DataFrame (and is also saved in hs.results):

Gene	C	Z	Pval	FDR
ENSG00000139644	0.069	10.527	3.21e-26	7.45e-25
ENSG00000179218	0.071	10.521	3.43e-26	7.93e-25
ENSG00000196139	0.081	10.517	3.59e-26	8.28e-25
ENSG00000119801	0.062	10.515	3.68e-26	8.48e-25
ENSG00000233355	0.058	10.503	4.15e-26	9.55e-25
...	...	...	...	...

Columns are:

• C: Scaled -1:1 autocorrelation coeficients
• Z: Z-score for autocorrelation
• Pval: P-values computed from Z-scores
• FDR: Q-values using the Benjamini-Hochberg procedure

Evaluate pair-wise gene associations (gene local correlations)

To group genes into modules, we need to first evaluate their pair-wise local correlations

Better than regular correlations, these 'local' correlations also take into accounts associations where one gene, X, is expression 'near' another gene Y in the map. This can better resolve correlations between sparsely detected genes.

hs_genes = hs_results.loc[hs_results.FDR < 0.05].index # Select genes

local_correlations = hs.compute_local_correlations(hs_genes, jobs=4) # jobs for parallelization

Here we run only on a subset of genes as evaluating all pair-wise correlations is very expensive computationally. The autocorrelation ordering gives us a natural method to select the informative genes for this purpose.

The output is a genes x genes pandas DataFrame of Z-scores for the local correlation values between genes. The output is also stored in hs.local_correlation_z.

Group genes into modules

Now that pair-wise local correlations are calculated, we can group genes into modules.

To do this, a convenience method is included create_modules which performs agglomerative clustering.

modules = hs.create_modules(
    min_gene_threshold=30, core_only=True, fdr_threshold=0.05
)

A note on the arguments - agglomerative clustering proceeds by joining together genes with the highest pair-wise Z-score with the following caveats:

• If the FDR-adjusted p-value of the correlation between two branches exceeds fdr_threshold, then the branches are not merged.
• If two branches are two be merged and they are both have at least min_gene_threshold genes, then the branches are not merged. Further genes that would join to the resulting merged module smaller average correlations between genes, i.e. the least-dense module (if core_only=False)

This method was used to preserved substructure (nested modules) while still giving the analyst some control. However, since there are a lot of ways to do hierarchical clustering, you can also manually cluster using the gene-distances in hs.local_correlation_z

The output is a pandas Series that maps gene to module number. Unassigned genes are indicated with a module number of -1. The output is also stored in hs.modules

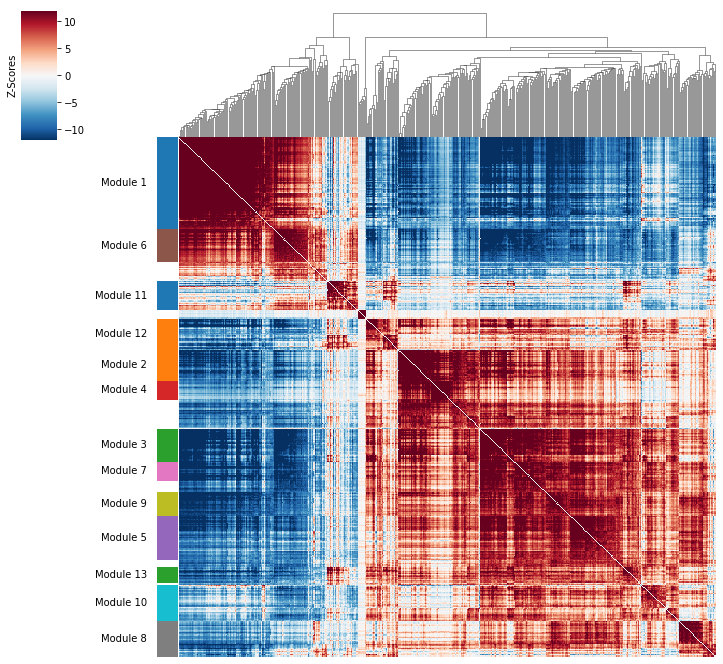
Correlation modules can be visualized by running hs.plot_local_correlations():

Compute summary per-cell module scores

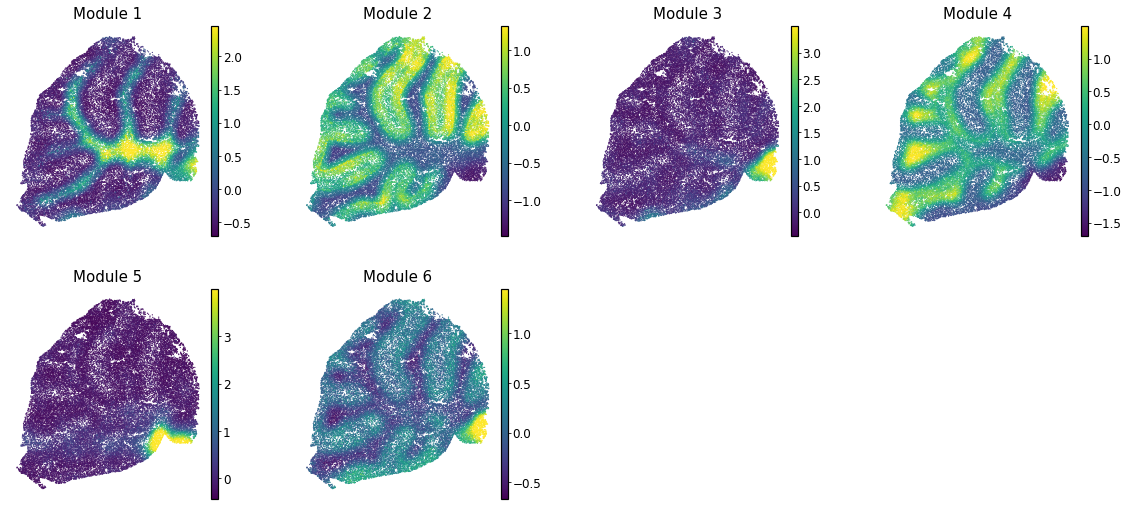
Finally, summary per-cell scores can be computed for a module. This is useful for visualizng the general pattern of expression for genes in a module.

module_scores = hs.calculate_module_scores()

The output is a pandas DataFrame (cells x modules) and is also saved in hs.module_scores

module_scores:

	1	2	3	4	5
AAACCCAAGGCCTAGA-1	0.785	-2.475	-1.407	-0.681	-1.882
AAACCCAGTCGTGCCA-1	-5.76	5.241	6.931	1.928	4.317
AAACCCATCGTGCATA-1	-2.619	3.572	0.143	1.832	1.585
AAACGAAGTAATGATG-1	-8.778	4.012	6.927	1.181	3.882
AAACGCTCATGCACTA-1	2.297	-2.517	-1.421	-1.102	-1.547
...	...	...	...	...	...

These can then be plotted onto other visual representations of the cells. For example, for spatial modules (from data in Rodriques et al, 2019) this looks like: