Compass is a toy language for compass & straightedge constructions, with easy syntax and visualization.
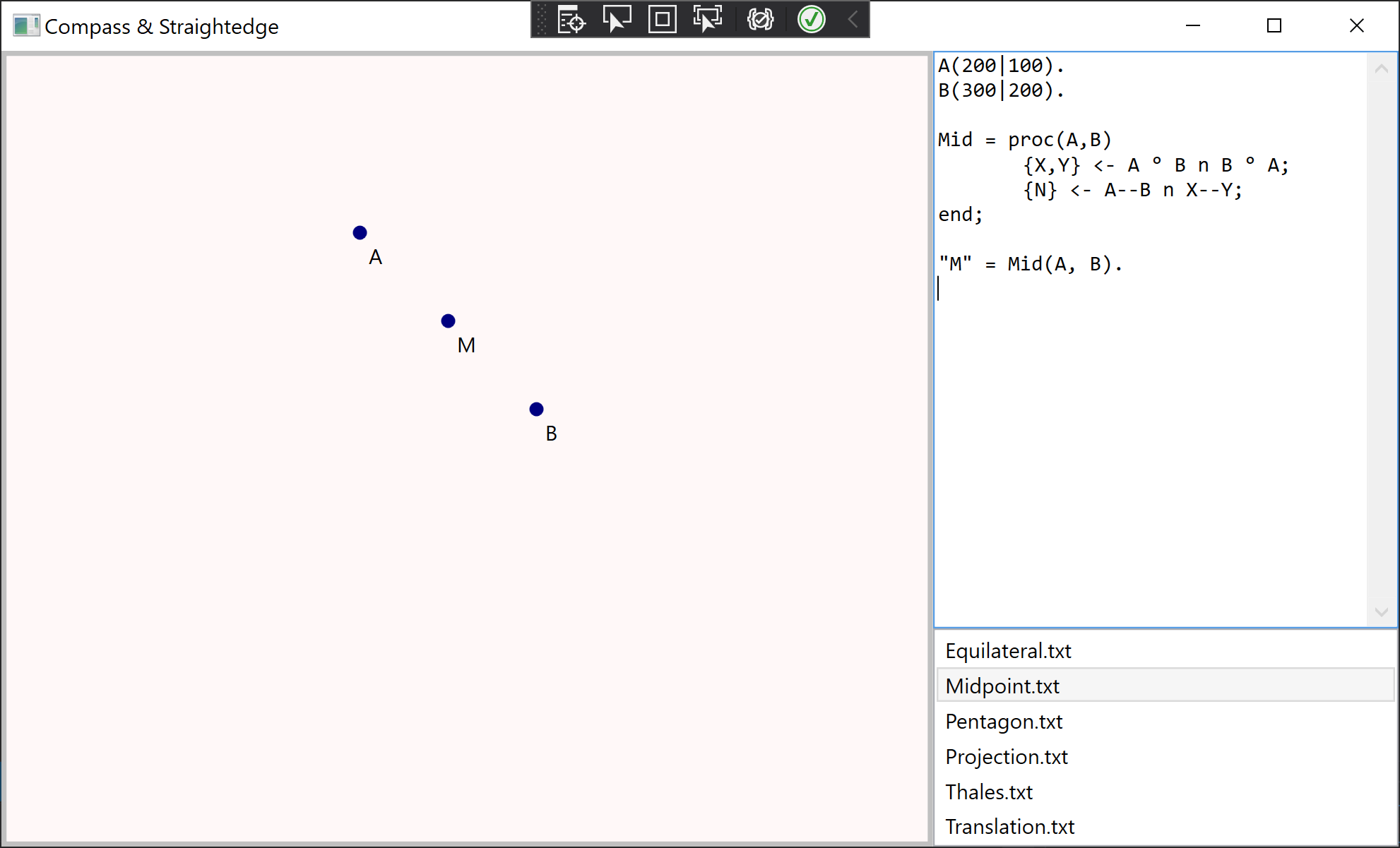
A(1|1), B(2|4). // define and name some points
C1 = A°B; // circle around A through B
C2 = B°A; // circle around B through A
{X1, X2} <- C1 n C2; // compute intersection of circles
{"M"} <- (X1-X2) n (C1-C2) // compute intersection of lines, giving the midpoint of A and BA Compass program consists of a sequence of statements, separated by commas, semicola or periods. A statement followed by ; is silenced, meaning its result will not be drawn. Otherwise, its result will be displayed.
Statements have the following forms
-
Named point definitions
A(20|50)defines a named pointed "A" and assigns it to the variable
A. A named point will, when drawn, have its name displayed alongside it. -
Assignments
X = <expr>Assigns to the variable
Xthe result of expression<expr>. Variables must begin with uppercase letters. The overall assignment evaluates to the variableX -
Pick assignments
{X1, ..., XN} = <expr>If
<expr>evaluates to a set, the pick assignment statement tries to pick N distinct elements from that set (in any order) and assigns them to variablesX1toXN. The overall assignment evaluates to the last variable assigned. One can (experimentally) pick from infinite sets such as circles and lines; the points thus obtained are random{A,B,C} <- M°P // pick three random points from a circle -
Bonus (Named assignments): If we put quotation marks around a variable in an assignment, if it is assigned a point, the point is upgraded to a named point as in
{"X"} <- Line1 n Line2This, together with Named point definitions, is the only way of creating named points.
Expressions have the following forms
Lines and segments
A-B // line segment AB
A->B // ray (half-line) from A through B
A--B // infinite line through A, B Circles
M°P // circle around M through P
M o P // alternative syntaxSet operations
A n B // intersection
A u B // union
A \ B // subtractionProcedures
// returns the midpoint between points A, B
Midpoint = proc(A,B)
{X,Y} <- (A°B) n (B°A)
{M} <- (X--Y) n (A--B)
endProcedure calls
Midpoint(A,B)
The datatypes currently supported in Compass are: Point, NamedPoint, Circle, Line, Ray, Segment, PointSet, Lambda
A list of examples is found in the Samples folder. The Compass application includes a sample browser.
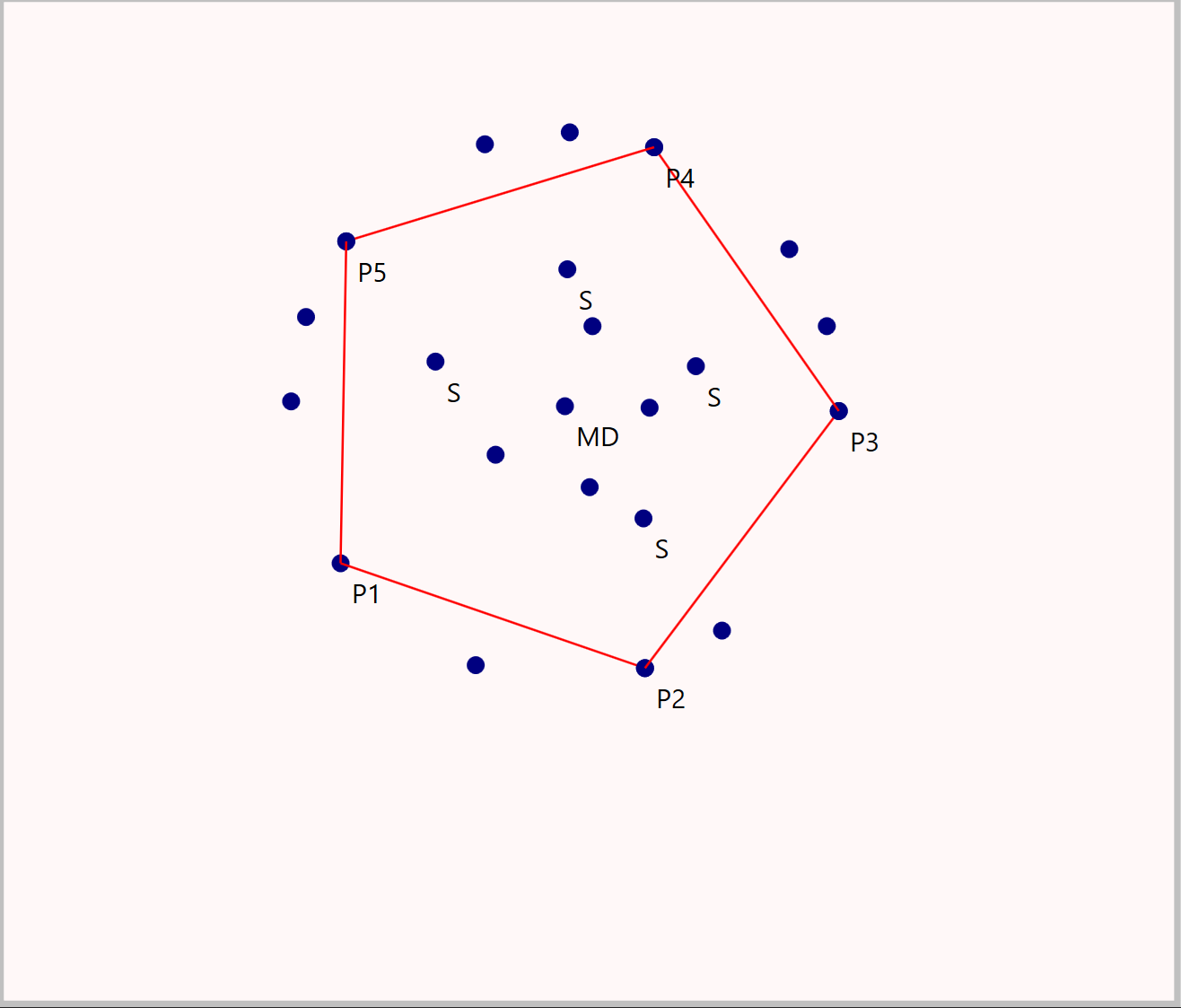
// Construction of a regular pentagon
MD(250|180), P1(150|250).
// midpoint between two points
Mid = proc(A,B)
{X,Y} <- A°B n B°A;
{R} <- (X--Y) n (A--B);
end;
// angle bisector
HalfAngle = proc(A,B,C)
{D} <- (A°B) n (A->C);
X = Mid(B,D);
A->X;
end;
// parallel line to A--B through P
Parallel = proc(P,A,B)
{X} <- P°A n A--B;
{Y} <- X°P n A--B;
{R} <- Y°X n P°A;
P--R;
end;
// make a 72° move from M-P
Penta = proc(M,P)
{Q} <- ((P--M) n M°P) \ {P}.
{X,Y} <- P°Q n Q°P;
{R} <- (X--Y) n M°P.
"S" = Mid(R,M).
{H} <- HalfAngle(S,M,P) n M--P.
{P2} <- Parallel(H,M,R) n M°P.
P-P2, P2;
end;
"P2" = Penta(MD,P1).
"P3" = Penta(MD,P2).
"P4" = Penta(MD,P3).
"P5" = Penta(MD,P4).
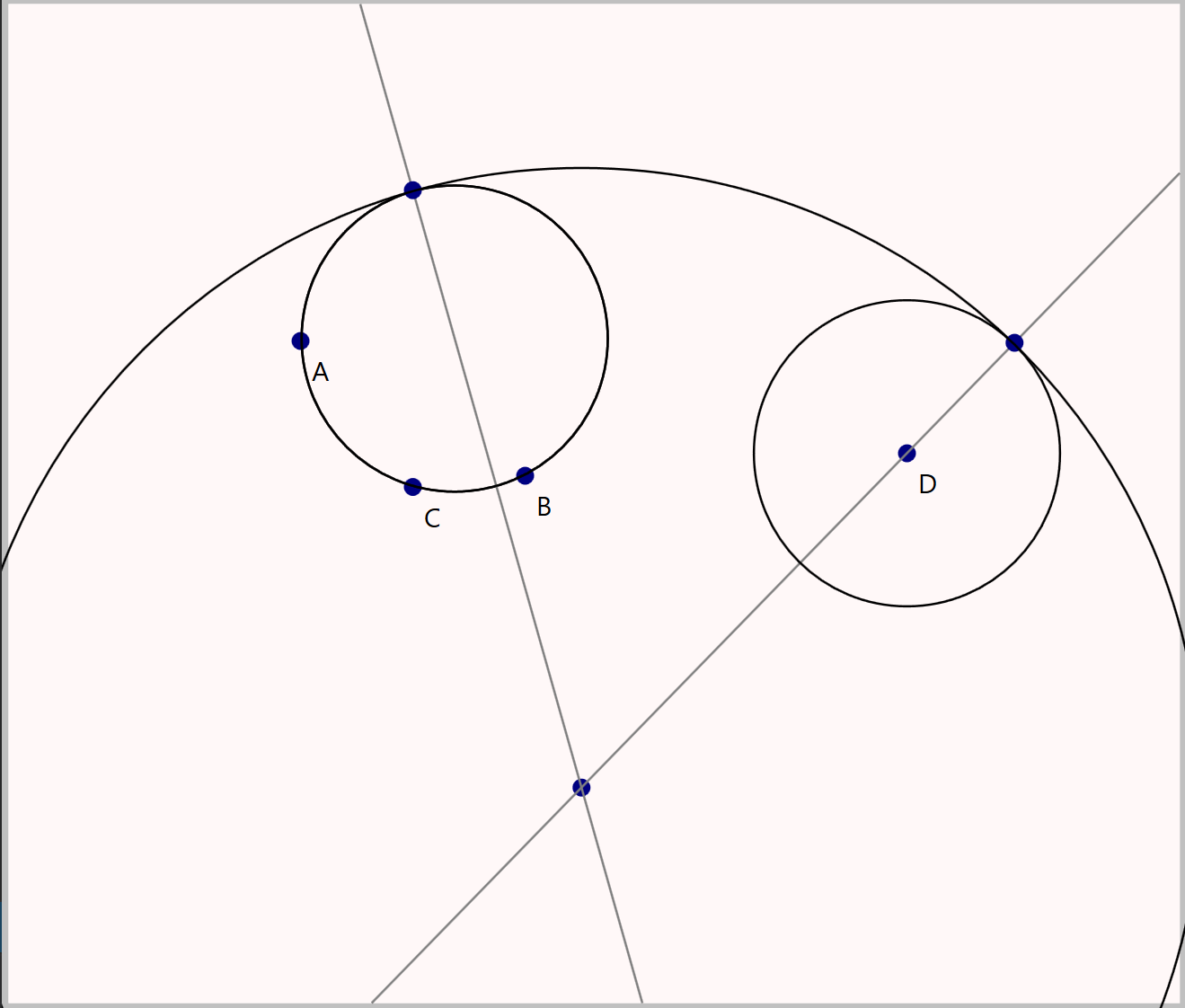
P5-P1.A(130|150), B(230|210), C(180|215), D(400|200).
Mid = proc(A,B)
{X,Y} <- A°B n B°A;
{M} <- (X--Y) n (A--B);
end;
Circle = proc(A,B,C)
{X,X'} <- A°B n B°A;
{Y,Y'} <- B°C n C°B;
{M} <- (X--X') n (Y--Y');
end;
Center = proc(C) {A,B,C} <- C; Circle(A,B,C); end;
CEQ = proc(A,B,C)
{D} <- A°B n B°A,
D--B, B°C,
{E} <- (D--B) n B°C,
D--A, D°E,
{F} <- (D--A) n D°E.
A°F;
end;
Move = proc(C,A)
M = Center(C);
{B} <- C;
CEQ(A,M,B);
end;
K = (Circle(A,B,C))°A.
Move(K,D).This is a very old hobby project. Its original goal was to test the interaction of F# with other .NET languages, parser combinators, definitional interpreters and the Visitor pattern, as well as doing some fun geometry.