Create 梳理RWKV 4，5(Eagle)，6(Finch)架构的区别以及个人理解和建议.md

BBuf · Apr 25, 2024 · b7fe0b2 · b7fe0b2
1 parent cd1786b
commit b7fe0b2
Showing 1 changed file with 309 additions and 0 deletions.
diff --git a/docs/academic/算法科普/Transformer/梳理RWKV 4，5(Eagle)，6(Finch)架构的区别以及个人理解和建议.md b/docs/academic/算法科普/Transformer/梳理RWKV 4，5(Eagle)，6(Finch)架构的区别以及个人理解和建议.md
@@ -0,0 +1,309 @@
+# 0x0. 前言
+RWKV系列模型的迭代速度比较快，主要是下面两篇paper：
+
+- RWKV: Reinventing RNNs for the Transformer Era： https://arxiv.org/abs/2305.13048 
+- Eagle and Finch: RWKV with Matrix-Valued States and Dynamic Recurrence：https://arxiv.org/abs/2404.05892
+
+之前我解析过RWKV-4的结构和代码实现（https://zhuanlan.zhihu.com/p/653327189），这里再把它和RWKV5，RWKV6放在一起进行对比解析一下。
+
+回顾一下，RWKV 4论文中对RWKV名字含义有说明：
+
+- R: Receptance vector acting as the acceptance of past information. 类似于LSTM的“门控单元”
+- W: Weight is the positional weight decay vector. A trainable model parameter. 可学习的位置权重衰减向量，什么叫“位置权重衰减”看下面的公式（14）
+- K: Key is a vector analogous to K in traditional attention. 与传统自注意力机制
+- V : Value is a vector analogous to V in traditional attention. 与传统自注意力机制相同
+
+> 如果不想看下面的细节，可以直接跳到结论那一节，我个人有一些尖锐的评价。
+## 0x1 RWKV 模型架构回顾
+RWKV模型由一系列RWKV Block模块堆叠而成，RWKV Block的结构如下图所示：
+
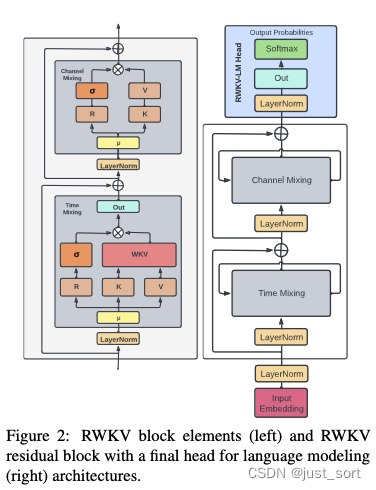+![在这里插入图片描述](https://img-blog.csdnimg.cn/fae4a854af104af4b467c4a3992161f5.png)
+
+RWKV Block又主要由Time Mixing和Channel Mixing组成。
+
+Time Mixing模块的公式定义如下：
+
+![在这里插入图片描述](https://img-blog.csdnimg.cn/366c0e9da102412482c850d641d4fb4f.png)
+
+这里的$t$表示当前时刻，$x_t$看成当前的token，而$x_{t-1}$看成前一个token，$r_t$、$k_t$、$v_t$的计算与传统Attention机制类似，通过将当前输入token与前一时刻输入token做线性插值，体现了recurrence的特性。然后$wkv_{t}$的计算则是对应注意力机制的实现，这个实现也是一个过去时刻信息与当前时刻信息的线性插值，注意到这里是指数形式并且当前token和之前的所有token都有一个指数衰减求和的关系，也正是因为这样让$wkv_{t}$拥有了线性attention的特性。
+
+然后RWKV模型里面除了使用Time Mixing建模这种Token间的关系之外，在Token内对应的隐藏层维度上RWKV也进行了建模，即通过Channel Mixing模块。
+
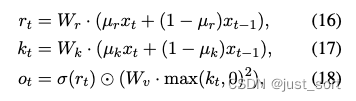+![在这里插入图片描述](https://img-blog.csdnimg.cn/f23f47399409438f957426d9e1fbad13.png)
+
+Channel Mixing的意思就是在特征维度上做融合。假设特征向量维度是d，那么每一个维度的元素都要接收其他维度的信息，来更新它自己。特征向量的每个维度就是一个“channel”（通道）。
+
+下图展示了RWKV模型整体的结构：
+
+
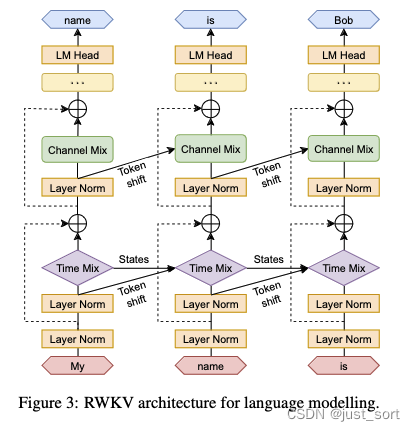+![在这里插入图片描述](https://img-blog.csdnimg.cn/66f843aca6304122acc7db378e278eed.png)
+
+这里提到的token shift就是上面对r, k, v计算的时候类似于卷积滑窗的过程。然后我们可以看到当前的token不仅仅可以通过Time Mixing的Token Shift和隐藏状态States（即$wkv_{t}$）和之前的token建立联系，也可以通过Channel Mixing的Token Shift和之前的token建立联系，类似于拥有了**全局感受野**。
+
+这里的讲解是以RWKV 4为例的，无论是RWKV的哪个版本，基本架构都是类似的，区别就在于对Time Mixing，Token shift以及Channel Mixing操作的修改。接下来的几节，就重点关注一下这个改动即可把握RWKV系列模型的进展。
+# 0x2. RWKV 4的具体实现
+主要关注Time Mixing，Channel Mixing，Token Shift的实现，代码实现见。https://github.com/BlinkDL/ChatRWKV/blob/main/RWKV_in_150_lines.py#L57-L93
+
+## 0x2.1 RWKV 4 Channel Mixing
+
+```python
+@torch.jit.script_method
+    def channel_mixing(self, x, state, i:int, time_mix_k, time_mix_r, kw, vw, rw):
+        xk = x * time_mix_k + state[5*i+0] * (1 - time_mix_k)
+        xr = x * time_mix_r + state[5*i+0] * (1 - time_mix_r)
+        state[5*i+0] = x
+        r = torch.sigmoid(rw @ xr)
+        k = torch.square(torch.relu(kw @ xk)) # square relu, primer paper
+        return r * (vw @ k)
+```
+
+参考RWKV 4 paper的Channel Mixing的公式来看：
+
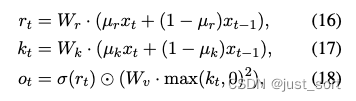+![在这里插入图片描述](https://img-blog.csdnimg.cn/f23f47399409438f957426d9e1fbad13.png)
+
+在channel_mixing函数里面，$x_t$对应当前token的词嵌入向量，$state[5*i+0]$表示前一个token的词嵌入向量。剩下的变量都是RWKV的可学习参数。然后代码里面会动态更新state，让$state[5*i+0]$总是当前token的前一个token的词嵌入。
+
+## 0x2.2 RWKV4 Time mixing函数
+
+```python
+@torch.jit.script_method
+    def time_mixing(self, x, state, i:int, time_mix_k, time_mix_v, time_mix_r, time_first, time_decay, kw, vw, rw, ow):
+        xk = x * time_mix_k + state[5*i+1] * (1 - time_mix_k) # 对应下面的公式12的后半部分
+        xv = x * time_mix_v + state[5*i+1] * (1 - time_mix_v) # 对应下面的公式13的后半部分
+        xr = x * time_mix_r + state[5*i+1] * (1 - time_mix_r) # 对应下图中的公式11的后半部分
+        state[5*i+1] = x
+        r = torch.sigmoid(rw @ xr) # 对应下面公式11的前半部分和公式15里的sigmoid
+        k = kw @ xk # 对应下面的公式12的前半部分
+        v = vw @ xv # 对应下面的公式13的前半部分
+
+        aa = state[5*i+2]
+        bb = state[5*i+3]
+        pp = state[5*i+4]
+        ww = time_first + k # 对应下面的RWKV可以写成递归形式图中的{u+k_t}
+        qq = torch.maximum(pp, ww) # 对应e^{u+k_t}的数值稳定性维护，维护最大值
+        e1 = torch.exp(pp - qq) 
+        e2 = torch.exp(ww - qq) # e1和e2分别对应分子分母的a_{t}和b_{t}的稳定性维护
+        a = e1 * aa + e2 * v
+        b = e1 * bb + e2
+        wkv = a / b # 对应wkv_t的计算
+        ww = pp + time_decay 
+        qq = torch.maximum(ww, k)
+        e1 = torch.exp(ww - qq) # 对应下面的RWKV可以写成递归形式图中的a_t计算的前半部分
+        e2 = torch.exp(k - qq) # 对应下面的RWKV可以写成递归形式图中的a_t计算的后半部分
+        state[5*i+2] = e1 * aa + e2 * v
+        state[5*i+3] = e1 * bb + e2
+        state[5*i+4] = qq
+        return ow @ (r * wkv)
+```
+
+仍然是要对照公式来看：
+
+![在这里插入图片描述](https://img-blog.csdnimg.cn/366c0e9da102412482c850d641d4fb4f.png)
+
+然后这里有一个trick，就是对$wkv_{t}$的计算可以写成RNN的递归形式：
+![在这里插入图片描述](https://img-blog.csdnimg.cn/18c378d6aa8c4e67a92b8e295ad9a90a.png)
+
+这样上面的公式就很清晰了，还需要注意的是在实现的时候由于有exp的存在，为了保证数值稳定性实现的时候减去了每个公式涉及到的e的指数部分的Max。
+
+关于RWKV 的attention部分（$wkv_{t}$）计算如果你有细节不清楚，建议观看一下这个视频：解密RWKV线性注意力的进化过程(https://www.bilibili.com/video/BV1zW4y1D7Qg/?spm_id_from=333.337.search-card.all.click&vd_source=4dffb0fbabed4311f4318e8c6d253a10) 。
+
+仔细理解上面的代码之后对照RWKV 5/6的公式理解后面的代码实现就不是很难了。
+# 0x3. RWKV Eagle (RWKV 5)的具体实现
+代码见：https://github.com/BlinkDL/ChatRWKV/blob/main/RWKV_v5_demo.py#L159-L195
+## 0x3.1 RWKV 5 Channel Mixing
+这个是RWKV 5的Channel Mixing的代码实现，可以对比一下RWKV 4的实现。
+```python
+@MyFunction
+    def channel_mixing(self, x, state, i:int, time_mix_k, time_mix_r, kw, vw, rw):
+        i0 = (2+self.head_size)*i+0
+        xk = x * time_mix_k + state[i0] * (1 - time_mix_k)
+        xr = x * time_mix_r + state[i0] * (1 - time_mix_r)
+        state[i0] = x
+        r = torch.sigmoid(rw @ xr)
+        k = torch.square(torch.relu(kw @ xk)) # square relu, primer paper
+        return r * (vw @ k)
+```
+RWKV 4的Channel Mixing的代码实现为：
+
+```python
+@torch.jit.script_method
+    def channel_mixing(self, x, state, i:int, time_mix_k, time_mix_r, kw, vw, rw):
+        xk = x * time_mix_k + state[5*i+0] * (1 - time_mix_k)
+        xr = x * time_mix_r + state[5*i+0] * (1 - time_mix_r)
+        state[5*i+0] = x
+        r = torch.sigmoid(rw @ xr)
+        k = torch.square(torch.relu(kw @ xk)) # square relu, primer paper
+        return r * (vw @ k)
+```
+这里的$i$表示的是RWKV有多少层，在RWKV4的每一层中Channel Mixing记录一个状态，而每一个Time Mixing则记录4个状态，所以一共是5个状态。而RWKV 5中每一层现在记录了`2+self.head_size`个状态，Channel Mixing记录的状态以及计算过程和RWKV 4是完全一样的。
+
+## 0x3.2 RWKV 5 Time Mixing
+
+```python
+@MyFunction
+    def time_mixing(self, x, state, i:int, time_mix_k, time_mix_v, time_mix_r, time_mix_g, time_first, time_decay, kw, vw, rw, gw, ow, ln_w, ln_b):
+        H = self.n_head
+        S = self.head_size
+
+        i1 = (2+S)*i+1
+        xk = x * time_mix_k + state[i1] * (1 - time_mix_k)
+        xv = x * time_mix_v + state[i1] * (1 - time_mix_v)
+        xr = x * time_mix_r + state[i1] * (1 - time_mix_r)
+        xg = x * time_mix_g + state[i1] * (1 - time_mix_g)
+        state[i1] = x
+
+        r = (rw @ xr).view(H, 1, S)
+        k = (kw @ xk).view(H, S, 1)
+        v = (vw @ xv).view(H, 1, S)
+        g = F.silu(gw @ xg)
+
+        s = state[(2+S)*i+2:(2+S)*(i+1), :].reshape(H, S, S)
+
+        x = torch.zeros(H, S)
+        a = k @ v
+        x = r @ (time_first * a + s)
+        s = a + time_decay * s
+
+        state[(2+S)*i+2:(2+S)*(i+1), :] = s.reshape(S, -1)
+        x = x.flatten()
+
+        x = F.group_norm(x.unsqueeze(0), num_groups=H, weight=ln_w, bias=ln_b, eps = 64e-5).squeeze(0) * g # same as gn(x/8, eps=1e-5)
+        return ow @ x
+```
+
+RWKV 5 Time Mixing的改动主要就在这个Time Mixing模块了，对应paper里面下面这一页：
+
+
+![在这里插入图片描述](https://img-blog.csdnimg.cn/direct/74d3bf50131c4e1fb1bd5622efd02e83.png)
+
+这里的最大的改进应该是现在的计算是分成了`H = self.n_head`个头，然后每个头的计算结果都被存到了state里。相比于RWKV-4，这种改进可以类比于Transformer的单头自注意力机制改到多头注意力机制。
+# 0x4. RWKV Finch (RWKV 6)的具体实现
+代码见：https://github.com/BlinkDL/ChatRWKV/blob/main/RWKV_v6_demo.py#L157-L199
+
+首先RWKV 6相比于RWKV 5在Token Shift上进行了改进，具体看下面的中间底部和右下角的图，分别是RWKV 4/5的Token Shift方式和RWKV 6的Token Shift方式。
+
+![在这里插入图片描述](https://img-blog.csdnimg.cn/direct/11bb409d719d4dfeb4b5cdac1b5f7fc5.png)
+Paper里面对RWKV 6的Token Shit也有详细描述：
+
+![在这里插入图片描述](https://img-blog.csdnimg.cn/direct/5464c9e84dee4b76ab75a6fec978b1bc.png)
+翻译一下：在Finch Token Shift中使用的$x_t$与$x_{t-1}$之间依赖数据的线性插值（ddlerp）定义如下：
+
+$lora□(x) = λ□ + tanh(x A□)B□$   ------------------------------------------ (14)
+
+$ddlerp□(a, b) = a + (b − a) ⊙ lora□(a + (b − a) ⊙ μ_x )$ -------------------------------------- (15)
+
+其中，$μ_x$ 和每个 $λ_□$ 引入了一个维度为D的可训练向量，每个 $A_□ ∈ R^{D×32}, B_□ ∈ R^{32×D}$ 引入了新的可训练权重矩阵。对于特殊情况$LoRA_ω$，我们引入了双倍大小的可训练权重矩阵 $A_ω ∈ R^{D×64}$, $B_ω ∈ R^{64×D}$。图示表示可以在上面的图1右下角找到。请注意，未来的7B及更大型的Finch模型预计将进一步增加这些权重矩阵的大小，翻倍或更多。
+
+这种新形式的Token Shift增强了数据依赖性，旨在扩展模型的能力，超出RWKV-4/Eagle风格的Token Shift，使得现在每个channel分配的新旧数据量取决于当前和之前时间步的输入。
+
+## 0x4.1 RWKV 6 Channel Mixing
+RWKV 6的Channel Mixing实现如下：
+```python
+def channel_mixing(self, x, state, i:int, time_maa_k, time_maa_r, kw, vw, rw):
+        i0 = (2+self.head_size)*i+0
+        sx = state[i0] - x
+        xk = x + sx * time_maa_k
+        xr = x + sx * time_maa_r
+        state[i0] = x
+        r = torch.sigmoid(rw @ xr)
+        k = torch.square(torch.relu(kw @ xk)) # square relu, primer paper
+        return r * (vw @ k)
+```
+相比于RWKV 5的Channel Mixing（见下面）来说，RWKV6的Channel Mixing没有变化，这里的`time_maa_k`和RWKV 5中的`time_mix_k`是相同形状的可学习参数，都是一个维度为$D$（模型的隐藏层维度）的张量。
+
+```python
+@MyFunction
+    def channel_mixing(self, x, state, i:int, time_mix_k, time_mix_r, kw, vw, rw):
+        i0 = (2+self.head_size)*i+0
+        xk = x * time_mix_k + state[i0] * (1 - time_mix_k)
+        xr = x * time_mix_r + state[i0] * (1 - time_mix_r)
+        state[i0] = x
+        r = torch.sigmoid(rw @ xr)
+        k = torch.square(torch.relu(kw @ xk)) # square relu, primer paper
+        return r * (vw @ k)
+```
+## 0x4.2 RWKV 6 Time Mixing
+RWKV 6相比于 RWKV 5主要是在在Time Mixing模块做了改进，具体见paper的下图：
+
+![在这里插入图片描述](https://img-blog.csdnimg.cn/direct/5c5813d53a7447aab0d669d288e17c9d.png)
+与Eagle中的情况不同，$w_t$在序列中不是静态的（见上面图1左侧和右上角的虚线箭头）。这是Finch中衰减核心变化的地方，因为现在$w_t$的每个channel都可以以依赖数据的方式独立随时间变化，而之前它是一个固定的学习向量。
+
+上述新的LoRA机制用于接收Eagle中看到的学习向量，并以低成本增加由传入输入确定的额外偏移。注意，LoRA过程本身使用的是Eagle风格的Token-Shifted值作为输入，不仅仅是最新的token。新的随时间变化的衰减$w_t$更进一步，之后再次应用LoRA。直观上，这是Token-Shifting的二阶变体，允许$w_t$的每个channel基于当前和先前token的混合变化，这种混合本身由两个token的各个方面决定。
+
+```python
+@MyFunction
+    def time_mixing(self, x, state, i:int, x_maa, w_maa, k_maa, v_maa, r_maa, g_maa, tm_w1, tm_w2, td_w1, td_w2, time_first, time_decay, kw, vw, rw, gw, ow, ln_w, ln_b):
+        H = self.n_head
+        S = self.head_size
+
+        i1 = (2+S)*i+1
+        sx = state[i1] - x
+        state[i1] = x
+        xxx = x + sx * x_maa
+        xxx = torch.tanh(xxx @ tm_w1).view(5, 1, -1)
+        xxx = torch.bmm(xxx, tm_w2).view(5, -1)
+        mw, mk, mv, mr, mg = xxx.unbind(dim=0)
+
+        xw = x + sx * (w_maa + mw)
+        xk = x + sx * (k_maa + mk)
+        xv = x + sx * (v_maa + mv)
+        xr = x + sx * (r_maa + mr)
+        xg = x + sx * (g_maa + mg)
+
+        w = (time_decay + (torch.tanh(xw @ td_w1) @ td_w2).float()).view(H, S, 1)
+        w = torch.exp(-torch.exp(w.float()))
+
+        r = (rw @ xr).view(H, 1, S)
+        k = (kw @ xk).view(H, S, 1)
+        v = (vw @ xv).view(H, 1, S)
+        g = F.silu(gw @ xg)
+
+        s = state[(2+S)*i+2:(2+S)*(i+1), :].reshape(H, S, S)
+
+        x = torch.zeros(H, S)
+        a = k @ v
+        x = r @ (time_first * a + s)
+        s = a + w * s
+
+        state[(2+S)*i+2:(2+S)*(i+1), :] = s.reshape(S, -1)
+        x = x.flatten()
+
+        x = F.group_norm(x.unsqueeze(0), num_groups=H, weight=ln_w, bias=ln_b, eps = 64e-5).squeeze(0) * g # same as gn(x/8, eps=1e-5)
+        return ow @ x
+```
+
+个人理解是RWKV 6在RWKV 5的基础上更激进的对Token Shift做出修改，结合了LoRA的实现方式让$w$也就是weight decay的每个channel都可以混合之前token的信息，而不是像RWKV 5那样做一个不变的整体参与计算。
+
+我只是非常粗浅的对RWKV的几个架构的实现进行了理解，总结起来就是RWKV 5和RWKV 6分别在注意力头数以及weight decay的可变性上做了改进，实现了更好的效果。
+
+# 0x5. HF源码对比
+上面的代码实际上有些抽象，HuggingFace版本的代码写得更好并且更直观一些，相关的变量命名也很规范，没有上面大量的鬼畜缩写符号。大家可以看下面RWKV 5/6链接指出的代码进行对比。
+
+RWKV 5：https://huggingface.co/RWKV/rwkv-5-world-3b/blob/main/modeling_rwkv5.py#L100-L213
+RWKV 6：https://huggingface.co/RWKV/rwkv-6-world-3b/blob/main/modeling_rwkv6.py#L179-L328
+
+# 0x6. 总结
+
+RWKV相比于LLama等开源大模型开发难度是更大的，因为它需要支持World HF Tokenizer以及各个版本独立的cuda kernel，但幸运的是在开源社区的努力下这些问题目前得到了部分解决。我个人也参与了一些开源项目，比如开发HF World Tokenizer以及HF RWKV 5/6 Model的 https://github.com/BBuf/RWKV-World-HF-Tokenizer ，然后为了将RWKV的cuda kernel更方便的应用在HF模型上面，我正在开发一个flash-rwkv库，让HF的模型可以通过一个pip安装的方式无感接入高性能的kernel，在微调和推理方面获得性能提升，也在探索kernel的优化：https://github.com/BBuf/flash-rwkv 。后续做出有用的东西再和大家分享。
+
+这篇文章主要是 从RWKV 4/5/6 的极简 Python 脚本的Channel Mixing和Time Mixing模块的代码角度对这几个架构做了探索，个人总结起来就是RWKV 5和RWKV 6分别在注意力头数以及weight decay的可变性上做了改进，实现了更好的效果。架构的改进好处是性能有大幅提升，但坏处是做工程的复杂度会剧增，例如对于推理框架来说就需要重新适配这个模型了。
+
+我也想吐槽几点，首先RWKV 5/6 Paper里面的8.3节Long Context Experiment是在4k长度下对比RWKV 4和RWKV 5/6的Loss，这个长度是不是太短了，可能说明不了什么。然后再长度外推以及更长序里的训练上没有看到实验，只看了训练更长的数据下相比于Flash Attention/Manba等架构的内存和速度优势，我觉得这个优势确实可以说出来但是是否需要先把比如128k长度这种超长文本的模型先做work。然后个人非常期待RWKV能在长文本上证明自己的价值，
+
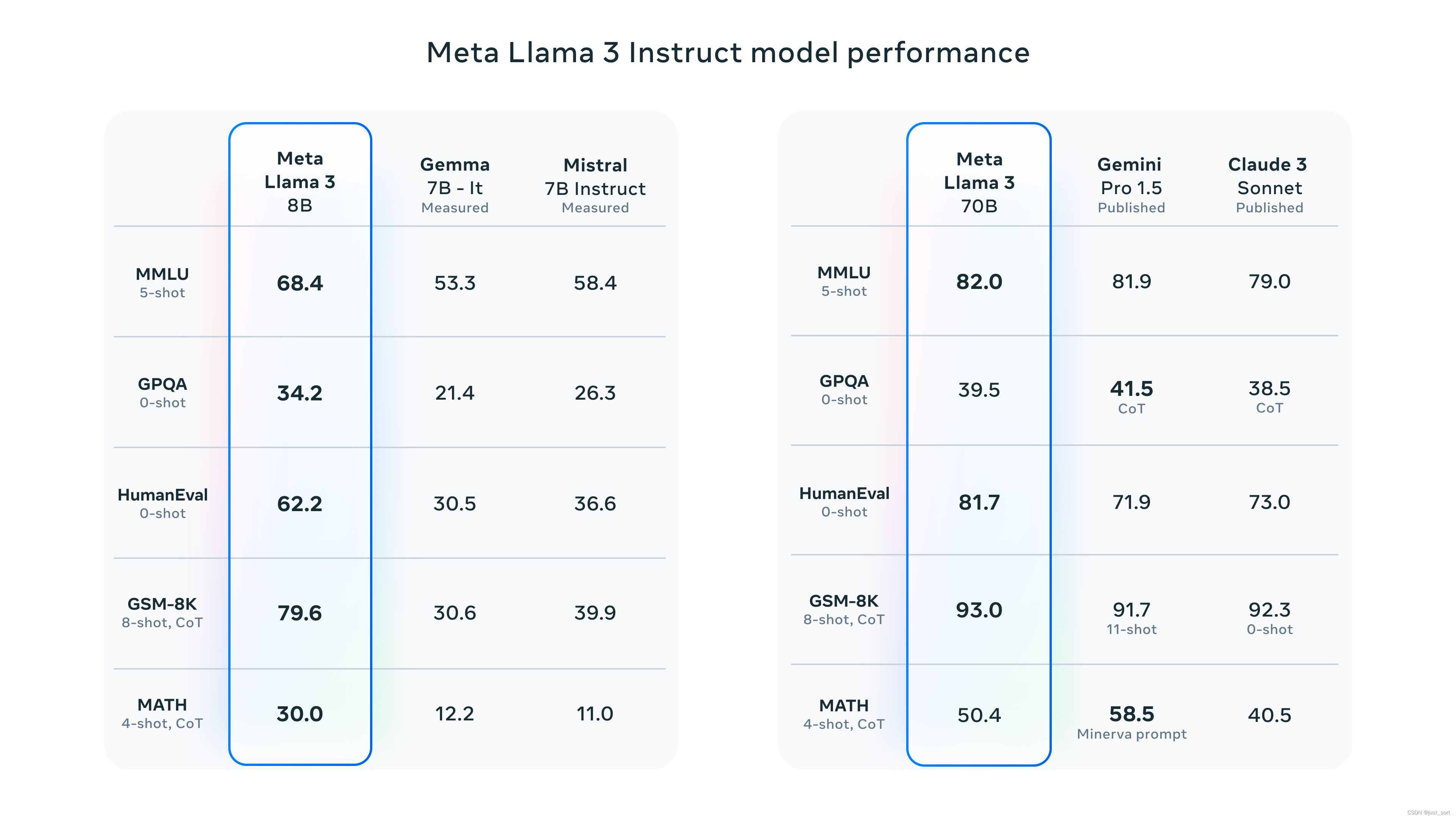
+还要吐槽一下Paper的第8节，目前大多数开源LLM的对比Benchmark应该是类似于LLama3这样，对比的是MMLU，GPQA，HumanEval，GSM-8K，MATH这些可以较为全面反应模型综合能力的Benchmark：
+
+![在这里插入图片描述](https://img-blog.csdnimg.cn/direct/f9dd083ffda747028b5cfc3640c08fcf.png)
+
+但RWKV 5/6里面对比的数据集虽然很多，但是我们读者一下无法把握它的真实水平，因为这里的类似太细了，会怀疑是不是专门跳的这些数据集做评测。
+
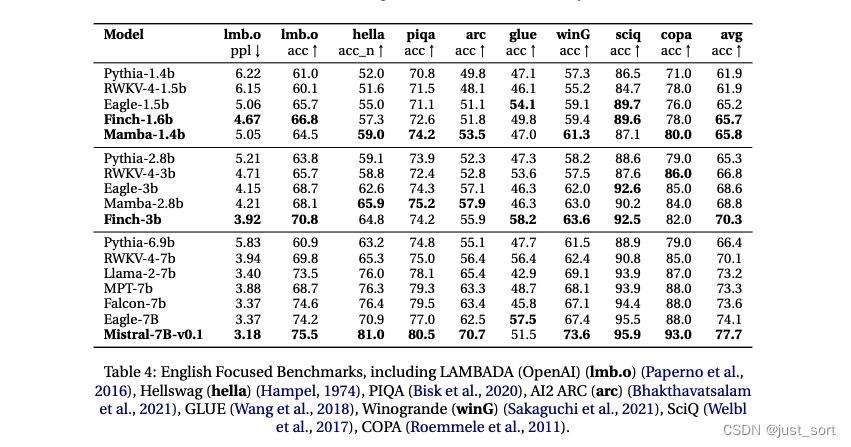+![](https://img-blog.csdnimg.cn/direct/6df857e8c11b41ba811fb4e277d0a3d8.png)
+因此，希望模型可以给出这几个指标的对比，当然在评测网站上比如OpenCompass进行公开对比也是可以的，以及大模型竞技场LMSys Arena。
+
+再吐槽一点，几乎每个做大模型的人都知道RWKV，Manba也好都是线性Attention的结构，速度快以及省显存的优势都知道，就没必要一直强调。现在关注的的是这个模型是否真的可以work，这就要求在权威Benchmark以及更长的Context Length训练上去展示这一点。
+
+
+最后，不得不承认RWKV的社区影响力已经让他成为一个成功的模型架构，但是能否走得更远则需要更多的努力，让我们拭目以待吧。
+
+
+
+