Skip to content

Latest commit

 

History

History
59 lines (53 loc) · 6.71 KB

32 Next Permutation 算法 字典序.md

File metadata and controls

59 lines (53 loc) · 6.71 KB

Implement next permutation, which rearranges numbers into the
lexicographically next greater permutation of numbers.

If such arrangement is not possible, it must rearrange it as the
lowest possible order (ie, sorted in ascending order).

The replacement must be in-place and use only constant extra memory.

Example:
1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1

题目

算法

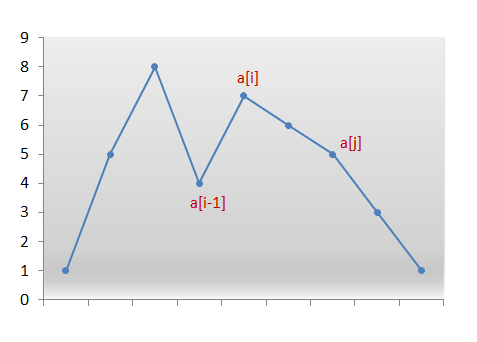
首先，我们观察到对于任何给定序列的降序，没有可能的下一个更大的排列。 我们需要从右边找到第一对两个连续的数字a[i]
和a[i−1]，它们满足 a[i]>a[i-1]。现在，没有对a[i−1]
右侧的重新排列可以创建更大的排列，因为该子数组由数字按降序组成。因此，我们需要重新排列a[i−1] 右边的数字，包括它自己。

现在，什么样子的重新排列将产生下一个更大的数字呢？我们想要创建比当前更大的排列。因此，我们需要将数字 a[i-1]
替换为位于其右侧区域的数字中比它更大的数字，例如 a[j]。

daiptionhere
我们交换数字 a[i-1] 和 a[j]。我们现在在索引 i-1 处有正确的数字。
但目前的排列仍然不是我们正在寻找的排列。我们需要通过仅使用 a[i-1]a[i−1]右边的数字来形成最小的排列。
因此，我们需要放置那些按升序排列的数字，以获得最小的排列。

但是，请记住，在从右侧扫描数字时，我们只是继续递减索引直到我们找到 a[i]和 a[i-1] 这对数。其中，a[i] >
a[i-1]。因此，a[i-1]a[i−1] 右边的所有数字都已按降序排序。此外，交换 a[i-1]和
a[j]并未改变该顺序。因此，我们只需要反转 a[i-1]之后的数字，以获得下一个最小的字典排列。

下面的动画将有助于你理解： enter image descriptionhere

class Solution:
    def nextPermutation(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        i = len(nums)-1
        #找到第一个后面比前面大的
        while i > 0 and nums[i] <= nums[i-1]:
            i-=1

    <span class="token keyword">if</span> i<span class="token punctuation">:</span><span class="token comment">#nums不是降序序列 一定存在直接后继</span>
        j <span class="token operator">=</span> i
        <span class="token comment">#找到第一个比nums[i]小的</span>
        <span class="token keyword">while</span> j <span class="token operator">&lt;</span> <span class="token builtin">len</span><span class="token punctuation">(</span>nums<span class="token punctuation">)</span><span class="token operator">-</span><span class="token number">1</span> <span class="token operator">and</span> nums<span class="token punctuation">[</span>j<span class="token operator">+</span><span class="token number">1</span><span class="token punctuation">]</span> <span class="token operator">&gt;</span> nums<span class="token punctuation">[</span>i<span class="token number">-1</span><span class="token punctuation">]</span><span class="token punctuation">:</span>
            j<span class="token operator">+=</span><span class="token number">1</span>
        <span class="token comment">#交换j和i-1</span>
        temp <span class="token operator">=</span> nums<span class="token punctuation">[</span>j<span class="token punctuation">]</span>
        nums<span class="token punctuation">[</span>j<span class="token punctuation">]</span> <span class="token operator">=</span> nums<span class="token punctuation">[</span>i<span class="token number">-1</span><span class="token punctuation">]</span>
        nums<span class="token punctuation">[</span>i<span class="token number">-1</span><span class="token punctuation">]</span> <span class="token operator">=</span> temp
        <span class="token comment">#把i后面的排序 说是排序 实际上已经是降序 只需要反转即可 时间复杂度是O(n)</span>
        nums<span class="token punctuation">[</span>i<span class="token punctuation">:</span><span class="token punctuation">]</span> <span class="token operator">=</span> <span class="token builtin">sorted</span><span class="token punctuation">(</span>nums<span class="token punctuation">[</span>i<span class="token punctuation">:</span><span class="token punctuation">]</span><span class="token punctuation">)</span>
    
    <span class="token keyword">else</span><span class="token punctuation">:</span><span class="token comment">#是降序序列 找到字典序最小的</span>
        nums <span class="token operator">=</span> nums<span class="token punctuation">.</span>sort<span class="token punctuation">(</span><span class="token punctuation">)</span>