statisticalinference_20191120_166_hwa.rmd

---
title: "15.6 Confidence intervals"
output: html_notebook
---

Confidence intervals are a very useful concept widely employed by data analysts. A version of these that are commonly seen come from the `ggplot` geometry `geom_smooth`. Here is an example using a temperature dataset available in R:
![geom_smooth](https://rafalab.github.io/dsbook/book_files/figure-html/first-confidence-intervals-example-1.png)
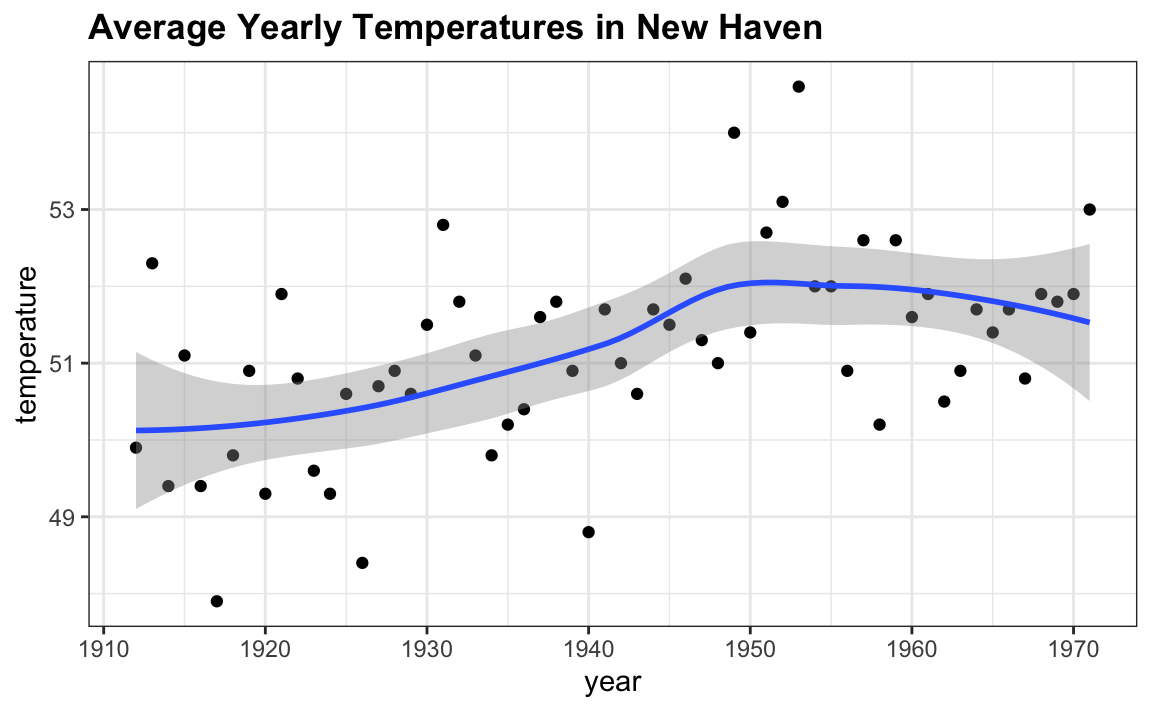
In the Machine Learning part we will learn how the curve is formed, but for now consider the shaded area around the curve. This is created using the concept of confidence intervals.

In our earlier competition, you were asked to give an interval. If the interval you submitted includes the $p$, you get half the money you spent on your "poll" back and pass to the next stage of the competition. One way to pass to the second round is to report a very large interval. For example, the interval $[0,1]$ is guaranteed to include $p$. However, with an interval this big, we have no chance of winning the competition. Similarly, if you are an election forecaster and predict the spread will be between -100% and 100%, you will be ridiculed for stating the obvious. Even a smaller interval, such as saying the spread will be between -10 and 10%, will not be considered serious. 

On the other hand, the smaller the interval we report, the smaller our chances are of winning the prize. Likewise, a bold pollster that reports very small intervals and misses the mark most of the time will not be considered a good pollster. We want to be somewhere in between.

We can use the statistical theory we have learned to compute the probability of any given interval including $p$.  If we are asked to create an interval with, say, a 95\% chance of including $p$, we can do that as well. These are called 95\% confidence intervals.

When a pollster reports an estimate and a margin of error, they are, in a way, reporting a 95\% confidence interval. Let's show how this works mathematically. 

We want to know the probability that the interval $[\bar{X} - 2\hat{\mbox{SE}}(\bar{X}), \bar{X} - 2\hat{\mbox{SE}}(\bar{X})]$ contains the true proportion $p$. First, consider that the start and end of these intervals are random variables: every time we take a sample, they change. To illustrate this, run the Monte Carlo simulation above twice. We use the same parameters as above:

```{r}
p <- 0.45
N <- 1000
```

And notice that the interval here:

```{r}
x <- sample(c(0, 1), size = N, replace = TRUE, prob = c(1-p, p))
x_hat <- mean(x)
se_hat <- sqrt(x_hat * (1 - x_hat) / N)
c(x_hat - 1.96 * se_hat, x_hat + 1.96 * se_hat)
```

is different from this one:

```{r}
x <- sample(c(0,1), size=N, replace=TRUE, prob=c(1-p, p))
x_hat <- mean(x)
se_hat <- sqrt(x_hat * (1 - x_hat) / N)
c(x_hat - 1.96 * se_hat, x_hat + 1.96 * se_hat)
```

Keep sampling and creating intervals and you will see the random variation.

To determine the probability that the interval includes $p$, we need to compute this:
$$
\mbox{Pr}\left(\bar{X} - 1.96\hat{\mbox{SE}}(\bar{X}) \leq p \leq \bar{X} + 1.96\hat{\mbox{SE}}(\bar{X})\right)
$$

By subtracting and dividing the same quantities in all parts of the equation, we
get that the above is equivalent to:
 
$$
\mbox{Pr}\left(-1.96 \leq \frac{\bar{X}- p}{\hat{\mbox{SE}}(\bar{X})} \leq  1.96\right)
$$

 
The term in the middle is an approximately normal random variable with expected value 0 and standard error 1, which we have been denoting with $Z$, so we have:

$$
\mbox{Pr}\left(-1.96 \leq Z \leq  1.96\right)
$$

which we can quickly compute using :

```{r}
pnorm(1.96) - pnorm(-1.96)
```

proving that we have a 95\% probability. 

If we want to have a larger probability, say 99\%, we need to multiply by whatever `z` satisfies the following:


$$
\mbox{Pr}\left(-z \leq Z \leq  z\right) = 0.99
$$

Using:

```{r}
z <- qnorm(0.995)
z
```

will achieve this because by definition `pnorm(qnorm(0.995))` is 0.995 and by symmetry `pnorm(1-qnorm(0.995))` is 1 - 0.995.  As a consequence, we have that:

```{r}
pnorm(z) - pnorm(-z)
```

is `0.995 - 0.005 = 0.99`. We can use this approach for any proportion $p$: we set `z = qnorm(1 - (1 - p)/2)` because $1 - (1 - p)/2 + (1 - p)/2 = p$. 

So, for example, for $p=0.95$, $1 - (1-p)/2 = 0.975$ and we get the 1.96 we have been using:

```{r}
qnorm(0.975)
```

### 15.6.1 A Monte Carlo simulation

We can run a Monte Carlo simulation to confirm that, in fact, a 95\% confidence interval includes $p$ 95\% of the time.

```{r}
N <- 1000
B <- 10000
inside <- replicate(B, {
  x <- sample(c(0,1), size = N, replace = TRUE, prob = c(1-p, p))
  x_hat <- mean(x)
  se_hat <- sqrt(x_hat * (1 - x_hat) / N)
  between(p, x_hat - 1.96 * se_hat, x_hat + 1.96 * se_hat)
})
mean(inside)
```


The following plot shows the first 100 confidence intervals. In this case, we created the simulation so the black line denotes the parameter we are trying to estimate:
![confidenceintervals](https://rafalab.github.io/dsbook/book_files/figure-html/confidence-interval-coverage-1.png)

### 15.6.2 The correct language

When using the theory we described above, it is important to remember that it is the intervals that are random, not $p$. In the plot above, we can see the random intervals moving around and $p$, represented with the vertical line, staying in the same place. The proportion of blue in the urn $p$ is not. So the 95\% relates to the probability that this random interval falls on top of $p$. Saying the $p$ has a 95\% chance of being between this and that is technically an incorrect statement because $p$ is not random. 

# 15.7 Exercises

For these exercises, we will use actual polls from the 2016 election. You can load the data from the __dslabs__ package.

```{r}
library(dslabs)
data("polls_us_election_2016")
```

Specifically, we will use all the national polls that ended within one week before the election.

```{r}
library(tidyverse)
polls <- polls_us_election_2016 %>% 
  filter(enddate >= "2016-10-31" & state == "U.S.") 
```

1\. For the first poll, you can obtain the samples size and estimated Clinton percentage with:

```{r}
N <- polls$samplesize[1]
x_hat <- polls$rawpoll_clinton[1]/100
```

Assume there are only two candidates and construct a 95% confidence interval for the election night proportion $p$. 

```{r}
se_hat <- sqrt(x_hat*(1-x_hat)/N)
ci <- c(x_hat - qnorm(0.975)*se_hat, x_hat + qnorm(0.975)*se_hat)
```

2\. Now use `dplyr` to add a confidence interval as two columns, call them `lower` and `upper`, to the object `poll`. Then use `select` to show the `pollster`, `enddate`, `x_hat`,`lower`, `upper` variables. Hint: define temporary columns `x_hat` and `se_hat`. 

```{r}
polls_p <- polls %>%
  mutate(x_hat = polls$rawpoll_clinton/100, se_hat = sqrt(x_hat*(1-x_hat)/polls$samplesize), lower = x_hat - qnorm(0.975)*se_hat, upper = x_hat + qnorm(0.975)*se_hat) %>% 
  select(pollster, enddate, x_hat, lower, upper)
```

3\. The final tally for the popular vote was Clinton 48.2%	and Trump 46.1%. Add a column, call it `hit`, to the previous table stating if the confidence interval included the true proportion $p=0.482$ or not. 
```{r}
polls_p <- polls_p %>% 
  mutate(hit = (lower<0.482 & upper>0.482))
polls_p
```

4\. For the table you just created, what proportion of confidence intervals included $p$?
```{r}
polls_p %>%
  summarize(mean(hit))
```

5\. If these confidence intervals are constructed correctly, and the theory holds up, what proportion should include $p$?

Answer : **0.95**

6\. A much smaller proportion of the polls than expected produce confidence intervals containing $p$. If you look closely at the table, you will see that most polls that fail to include $p$ are underestimating. The reason for this is undecided voters, individuals polled that do not yet know who they will vote for or do not want to say. 
Because, historically, undecideds divide evenly between the two main candidates on election day, it is more informative to estimate the spread or the difference between the proportion of two candidates $d$, which in this election was $0. 482 - 0.461 = 0.021$. 
Assume that there are only two parties and that $d = 2p - 1$, redefine `polls` as below and
re-do exercise 1, but for the difference.

```{r}
polls <- polls_us_election_2016 %>% 
  filter(enddate >= "2016-10-31" & state == "U.S.")  %>%
  mutate(d_hat = rawpoll_clinton / 100 - rawpoll_trump / 100)

N <- polls$samplesize[1]
d_hat <- polls$d_hat[1]

x_hat <- (d_hat+1)/2
se_hat <- 2*sqrt(x_hat*(1-x_hat)/N)
ci <- c(d_hat - qnorm(0.975)*se_hat, d_hat + qnorm(0.975)*se_hat)

se_hat
```

7\. Now repeat exercise 3, but for the difference.
```{r}
polls_d <- polls %>% 
  mutate(x_hat = (d_hat + 1) / 2 , se_hat = 2 * sqrt(x_hat * (1 - x_hat) / samplesize), lower = d_hat - qnorm(0.975) * se_hat, upper = d_hat + qnorm(0.975) * se_hat, hit=lower <= 0.021 & upper >= 0.021) %>%
  select(pollster, enddate, d_hat, lower, upper, hit)

polls_d
```

8\. Now repeat exercise 4, but for the difference.
```{r}
polls_d %>%
  summarize(mean(hit))
```

9\. Although the proportion of confidence intervals goes up substantially, it is still lower than 0.95. In the next chapter, we learn the reason for this. To motivate this, make a plot of the error, the difference between each poll's estimate and the actual $d=0.021$. Stratify by pollster.
```{r fig.height=9, fig.width=16}
polls %>% 
  mutate(error = d_hat - 0.021) %>% 
  ggplot(aes(pollster, error)) + 
  geom_point() +
  coord_flip()
```

10\. Redo the plot that you made for exercise 9, but only for pollsters that took five or more polls.
```{r fig.height=9, fig.width=16}
polls %>% 
  mutate(error = d_hat - 0.021) %>% 
  group_by(pollster) %>%
  filter(n() >= 5) %>%
  ggplot(aes(pollster, error)) + 
  geom_point() +
  coord_flip()
```

# 15.8 Power

Pollsters are not successful at providing correct confidence intervals, but rather at predicting who will win. When we took a 25 bead sample size, the confidence interval for the spread:

```{r}
N <- 25
x_hat <- 0.48
(2 * x_hat - 1) + c(-1.96, 1.96) * 2 * sqrt(x_hat * (1 - x_hat) / N)
```

includes 0. If this were a poll and we were forced to make a declaration, we would have to say it was a "toss-up". 

A problem with our poll results is that given the sample size and the value of $p$, we would have to sacrifice on the probability of an incorrect call to create an interval that does not include 0. 

This does not mean that the election is close. It only means that we have a small sample size. In statistical textbooks this is called lack of _power_. In the context of polls, _power_ is the probability of detecting spreads different from 0.  

By increasing our sample size, we lower our standard error and therefore have a much better chance of detecting the direction of the spread.

# 15.9 p-values

p-values are ubiquitous in the scientific literature. They are related to confidence intervals so we introduce the concept here. 

Let's consider the blue and red beads. Suppose that rather than wanting an estimate of the spread or the proportion of blue, I am interested only in the question: are there more blue beads or red beads? I want to know if the spread $2p-1 > 0$. 

Say we take a random sample of $N=100$ and we observe $52$ blue beads, which gives us $2\bar{X}-1=0.04$. This seems to be pointing to the existence of more blue than red beads since 0.04 is larger than 0. However, as data scientists we need to be skeptical. We know there is chance involved in this process and we could get a 52 even when the actual spread is 0.
We call the assumption that the spread is $2p-1=0$ a _null hypothesis_. The null hypothesis is the skeptic's hypothesis. We have observed a random variable $2*\bar{X}-1 = 0.04$ and the p-value is the answer to the question: how likely is it to see a value this large, when the null hypothesis is true? So we write:

$$
\mbox{Pr}(\mid \bar{X} - 0.5 \mid > 0.02 )
$$

assuming the $2p-1=0$ or $p=0.5$. Under the null hypothesis we know that:

$$
\sqrt{N}\frac{\bar{X} - 0.5}{\sqrt{0.5(1-0.5)}}
$$

is standard normal. We therefore can compute the probability above, which is the p-value.

$$
\mbox{Pr}\left(\sqrt{N}\frac{\mid \bar{X} - 0.5\mid}{\sqrt{0.5(1-0.5)}} > \sqrt{N} \frac{0.02}{ \sqrt{0.5(1-0.5)}}\right)
$$


```{r}
N <- 100
z <- sqrt(N)*0.02/0.5
1 - (pnorm(z) - pnorm(-z))
```

In this case, there is actually a large chance of seeing 52 or larger under the null hypothesis. 

Keep in mind that there is a close connection between p-values and confidence intervals. If a 95% confidence interval of the spread does not include 0, we know that the p-value must be smaller than 0.05. 

To learn more about p-values, you can consult any statistics textbook. However, in general, we prefer reporting confidence intervals over p-values since it gives us an idea of the size of the estimate. If we just report the p-value we provide no information about the significance of the finding in the context of the problem.

# 15.10 Association tests

The statistical tests we have studied up to now leave out a
substantial portion of data types. Specifically, we have not discussed inference for binary, categorical, and ordinal data. To give a very specific example, consider the following case study.


A 2014 PNAS paper analyzed success rates from funding agencies in the Netherlands and concluded that their:

> results reveal gender bias favoring male applicants over female applicants in the prioritization of their "quality of researcher" (but not "quality of proposal") evaluations and success rates, as well as in the language use in instructional and evaluation materials.

The main evidence for this conclusion comes down to a comparison of the percentages. Table S1 in the paper includes the information we need. Here are the three columns showing the overall outcomes:

```{r}
library(tidyverse)
library(dslabs)
data("research_funding_rates")
research_funding_rates %>% select(discipline, applications_total, success_rates_total) %>% head()
```

We have these values for each gender:
```{r}
names(research_funding_rates)
```

We can compute the totals that were successful and the totals that were not as follows:

```{r}
totals <- research_funding_rates %>% 
  select(-discipline) %>% 
  summarize_all(sum) %>%
  summarize(yes_men = awards_men, 
            no_men = applications_men - awards_men, 
            yes_women = awards_women, 
            no_women = applications_women - awards_women) 
```

So we see that a larger percent of men than women received awards:

```{r}
totals %>% summarize(percent_men = yes_men/(yes_men+no_men),
                     percent_women = yes_women/(yes_women+no_women))
```

But could this be due just to random variability? 
Here we learn how to perform inference for this type of data.

### 15.10.1 Lady Tasting Tea

R.A. Fisher was one of the first to formalize hypothesis testing. The "Lady Tasting Tea" is one of the most famous examples. 

The story is as follows: an acquaintance of Fisher's claimed that she could tell if milk was added before or after tea was poured. Fisher was skeptical. He designed an experiment to test this claim. He gave her four pairs of
cups of tea: one with milk poured first, the other after. The order
was randomized. The null hypothesis here is that she is guessing. Fisher derived the distribution for the number of correct picks on the assumption that the choices were random and independent.

As an example, suppose she picked 3 out of 4 correctly. Do we believe
she has a special ability? The basic question we ask is: if the tester is actually guessing, what
are the chances that she gets 3 or more correct? Just as we have done
before, we can compute a probability under the null hypothesis that she
is guessing 4 of each. Under this null hypothesis, we can
think of this particular example as picking 4 balls out of an urn
with 4 blue (correct answer) and 4 red (incorrect answer) balls. Remember, she knows that there are four before tea and four after.

Under the null hypothesis that she is simply guessing, each ball
has the same chance of being picked. We can then use combinations to
figure out each probability. The probability of picking 3 is
${4 \choose 3} {4 \choose 1} / {8 \choose 4} = 16/70$. The probability of
picking all 4 correct is
${4 \choose 4} {4 \choose 0}/{8 \choose 4}= 1/70$.
Thus, the chance of observing a 3 or something more extreme,
under the null hypothesis, is $\approx 0.24$. This is the p-value. The procedure that produced this p-value is called _Fisher's exact test_ and it uses the *hypergeometric distribution*. 

### 15.10.2 Two-by-two tables

The data from the experiment is usually summarized by a table like this:

```{r}
tab <- matrix(c(3,1,1,3),2,2)
rownames(tab)<-c("Poured Before","Poured After")
colnames(tab)<-c("Guessed before","Guessed after")
tab
```

These are referred to as a two-by-two table. For each of the four combinations one can get with a pair of binary variables, they show the observed counts for each occurrence.

The function `fisher.test` performs the inference calculations above:

```{r}
fisher.test(tab, alternative="greater")$p.value
```

### 15.10.3 Chi-square Test

Notice that, in a way, our funding rates example is similar to the Lady Tasting Tea. However, in the Lady Tasting Tea example, the number of blue and red beads is experimentally fixed and the number of answers given for each category is also fixed. This is because Fisher made sure there were four cups with milk poured before tea and four cups with milk poured after and the lady knew this, so the answers would also have to include four befores and four afters. If this is the case, the sum of the rows and the sum of the columns are fixed. This defines constraints on the possible ways we can fill the two
by two table and also permits us to use the hypergeometric
distribution. In general, this is not the case. Nonetheless, there is
another approach, the Chi-squared test, which is described below. 
Imagine we have `r prettyNum(totals, ,big.mark=",")` applicants, some are men and some are women and some get funded, whereas others don't. We saw that the success rates for men and woman were:

```{r}
totals %>% summarize(percent_men = yes_men/(yes_men+no_men),
                     percent_women = yes_women/(yes_women+no_women))
```

respectively. Would we see this again if we randomly assign funding at the overall rate:

```{r}
rate <- totals %>%
  summarize(percent_total = 
              (yes_men + yes_women)/
              (yes_men + no_men +yes_women + no_women)) %>%
  pull(percent_total)
rate
```

The Chi-square test answers this question. The first step is to create the two-by-two data table:

```{r}
two_by_two <- data.frame(awarded = c("no", "yes"), 
                     men = c(totals$no_men, totals$yes_men),
                     women = c(totals$no_women, totals$yes_women))
two_by_two
```

The general idea of the Chi-square test is to compare this two-by-two table to what you expect to see, which would be:

```{r}
data.frame(awarded = c("no", "yes"), 
       men = (totals$no_men + totals$yes_men) * c(1 - rate, rate),
       women = (totals$no_women + totals$yes_women) * c(1 - rate, rate))
```

We can see that more men than expected and fewer women than expected received funding. However, under the null hypothesis these observations are random variables. The Chi-square test tells us how likely it is to see
a deviation this large or larger. This test uses an asymptotic result, similar to the CLT, related to the sums of independent binary outcomes. 
The R function `chisq.test` takes a two-by-two table and returns the results from the test:

```{r}
chisq_test <- two_by_two %>% select(-awarded) %>% chisq.test()
```

We see that the p-value is 0.0509:

```{r}
chisq_test$p.value
```

### 15.10.4 The odds ratio

An informative summary statistic associated with two-by-two tables is the odds ratio. Define the two variables as $X = 1$ if you are a male and 0 otherwise, and $Y=1$ if you are funded and 0 otherwise. The odds of getting funded if you are a man is defined:

$$\mbox{Pr}(Y=1 \mid X=1) / \mbox{Pr}(Y=0 \mid X=1)$$

and can be computed like this:
```{r}
odds_men <- with(two_by_two, (men[2]/sum(men)) / (men[1]/sum(men)))
odds_men
```

And the odds of being funded if you are a woman is:


$$\mbox{Pr}(Y=1 \mid X=0) / \mbox{Pr}(Y=0 \mid X=0)$$


and can be computed like this:
```{r}
odds_women <- with(two_by_two, (women[2]/sum(women)) / (women[1]/sum(women)))
odds_women
```

The odds ratio is the ratio for these two odds: how many times larger are the odds for men than for women?

```{r}
odds_men / odds_women
```

We often see two-by-two tables written out as 

|   |Men|Women|
|---|---|-----|
|Awarded|a|b|
|Not Awarded|c|d|

In this case, the odds ratio is $\frac{a/c}{b/d}$
which is equivalent to $(ad) / (bc)$

### 15.10.5 Confidence intervals for the odds ratio

Computing confidence intervals for the odds ratio is not mathematically straightforward. Unlike other statistics, for which we can derive useful approximations of their distributions, the odds ratio is not only a
ratio, but a ratio of ratios. Therefore, there is no simple way of
using, for example, the CLT. 
  
However, statistical theory tells us that when all four entries of the two-by-two table are large enough, then the log of the odds ratio is approximately normal with standard error 

$$
\sqrt{1/a + 1/b + 1/c + 1/d} 
$$

This implies that a 95% confidence interval for the log odds ratio can be formed by:

$$
\log\left(\frac{ad}{bc}\right) \pm 1.96 \sqrt{1/a + 1/b + 1/c + 1/d} 
$$

By exponentiating these two numbers we can construct a confidence interval of the odds ratio. 

Using R we can compute this confidence interval as follows:
```{r}
log_or <- log(odds_men / odds_women)
se <- two_by_two %>% select(-awarded) %>%
  summarize(se = sqrt(sum(1/men) + sum(1/women))) %>%
  pull(se)
ci <- log_or + c(-1,1) * qnorm(0.975) * se
```

If we want to convert it back to the odds ratio scale, we can exponentiate:

```{r}
exp(ci)
```

Note that 1 is not included in the confidence interval which must mean that the p-value is smaller than 0.05. We can confirm this using:

```{r}
2*(1 - pnorm(log_or, 0, se))
```

This is a slightly different p-value than that with the Chi-square test. This is because we are using a different asymptotic approximation to the null distribution. To learn more about inference and asymptotic theory for odds ratio, consult the _Generalized Linear Models_ book by
McCullagh and Nelder.

### 15.10.6 Small count correction

Note that the log odds ratio is not defined if any of the cells of the two-by-two table is 0. This is because if $a$, $b$, $c$, or $d$ is 0, the $\log(\frac{ad}{bc})$ is either the log of 0 or has a 0 in the denominator. For this situation, it is common practice to avoid 0s by adding 0.5 to each cell. This is referred to as the _Haldane–Anscombe correction_ and has been shown, both in practice and theory, to work well.

### 15.10.7 Large samples, small p-values

As mentioned earlier, reporting only p-values is not an appropriate
way to report the results of data analysis. In scientific journals, for example, 
some studies seem to overemphasize p-values. Some of these studies have large sample sizes
and report impressively small p-values.  Yet when one looks closely at
the results, we realize odds ratios are quite modest: barely bigger
than 1. In this case the difference may not be *practically significant* or *scientifically significant*.

Note that the relationship between odds ratio and p-value is not one-to-one. It depends on the sample size. So a very small p-value does not necessarily mean a very large odds ratio.
Notice what happens to the p-value if we multiply our two-by-two table by 10, which does not change the odds ratio:

```{r}
two_by_two %>% select(-awarded) %>%
  mutate(men = men*10, women = women*10) %>%
  chisq.test() %>% .$p.value
```


# 15.11 Exercises

1\. A famous athlete has an impressive career, winning 70% of her 500 career matches. However, this athlete gets criticized because in important events, such as the Olympics, she has a losing record of 8 wins and 9 losses. Perform a Chi-square test to determine if this losing record can be simply due to chance as opposed to not performing well under pressure.

```{r}
two_by_two <- data.frame(record = c('wins', 'losses'), important_events = c(8, 9), normal_events = c(350-8, 150-9))
chisq_test <- two_by_two %>% select(-record) %>% chisq.test()
chisq_test$p.value
```

2\. Why did we use the Chi-square test instead of Fisher's exact test in the previous exercise?

a. It actually does not matter, since they give the exact same p-value.
b. Fisher's exact and the Chi-square are different names for the same test.
c. Because the sum of the rows and columns of the two-by-two table are not fixed so the hypergeometric distribution is not an appropriate assumption for the null hypothesis. For this reason, Fisher's exact test is rarely applicable with observational data.
d. Because the Chi-square test runs faster.

Answer : **C**

3\. Compute the odds ratio of "losing under pressure" along with a confidence interval.

```{r}
odds_important_events <- with(two_by_two, (important_events[1]/sum(important_events)) / (important_events[2]/sum(important_events)))
odds_normal_events <- with(two_by_two, (normal_events[1]/sum(normal_events)) / (normal_events[2]/sum(normal_events)))
log_or <- log(odds_important_events / odds_normal_events)
se <- two_by_two %>% select(-record) %>%
  summarize(se = sqrt(sum(1/important_events) + sum(1/normal_events))) %>%
  pull(se)
ci <- log_or + c(-1,1) * qnorm(0.975) * se
exp(ci)
```
  
4\. Notice that the p-value is larger than 0.05 but the 95% confidence interval does not include 1. What explains this?

a. We made a mistake in our code.
b. These are not t-tests so the connection between p-value and confidence intervals does not apply.
c. Different approximations are used for the p-value and the confidence interval calculation. If we had a larger sample size the match would be better.
d. We should use the Fisher exact test to get confidence intervals.

Answer: **C**

5\. Multiply the two-by-two table by 2 and see if the p-value and confidence retrieval are a better match.

```{r}
two_by_two %>% select(-record) %>%
  mutate(important_events = important_events*2, normal_events = normal_events*2) %>%
  chisq.test() %>% .$p.value
```