给你一个大小为 m x n 的整数矩阵 grid 。
按以下形式将矩阵的一部分定义为一个 沙漏 :
返回沙漏中元素的 最大 总和。
注意:沙漏无法旋转且必须整个包含在矩阵中。
示例 1:
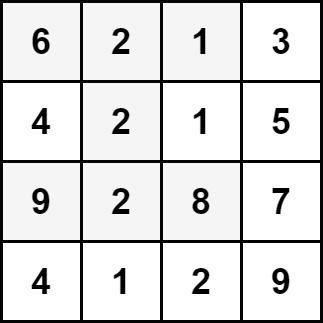
输入:grid = [[6,2,1,3],[4,2,1,5],[9,2,8,7],[4,1,2,9]] 输出:30 解释:上图中的单元格表示元素总和最大的沙漏:6 + 2 + 1 + 2 + 9 + 2 + 8 = 30 。
示例 2:
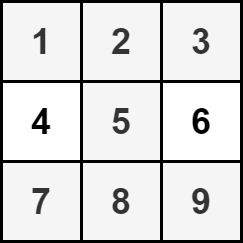
输入:grid = [[1,2,3],[4,5,6],[7,8,9]] 输出:35 解释:上图中的单元格表示元素总和最大的沙漏:1 + 2 + 3 + 5 + 7 + 8 + 9 = 35 。
提示:
m == grid.lengthn == grid[i].length3 <= m, n <= 1500 <= grid[i][j] <= 106
方法一:枚举
我们观察题目发现,每个沙漏就是一个
时间复杂度
class Solution:
def maxSum(self, grid: List[List[int]]) -> int:
m, n = len(grid), len(grid[0])
ans = 0
for i in range(1, m - 1):
for j in range(1, n - 1):
s = -grid[i][j - 1] - grid[i][j + 1]
s += sum(grid[x][y] for x in range(i - 1, i + 2)
for y in range(j - 1, j + 2))
ans = max(ans, s)
return ansclass Solution {
public int maxSum(int[][] grid) {
int m = grid.length, n = grid[0].length;
int ans = 0;
for (int i = 1; i < m - 1; ++i) {
for (int j = 1; j < n - 1; ++j) {
int s = -grid[i][j - 1] - grid[i][j + 1];
for (int x = i - 1; x <= i + 1; ++x) {
for (int y = j - 1; y <= j + 1; ++y) {
s += grid[x][y];
}
}
ans = Math.max(ans, s);
}
}
return ans;
}
}class Solution {
public:
int maxSum(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
int ans = 0;
for (int i = 1; i < m - 1; ++i) {
for (int j = 1; j < n - 1; ++j) {
int s = -grid[i][j - 1] - grid[i][j + 1];
for (int x = i - 1; x <= i + 1; ++x) {
for (int y = j - 1; y <= j + 1; ++y) {
s += grid[x][y];
}
}
ans = max(ans, s);
}
}
return ans;
}
};func maxSum(grid [][]int) (ans int) {
m, n := len(grid), len(grid[0])
for i := 1; i < m-1; i++ {
for j := 1; j < n-1; j++ {
s := -grid[i][j-1] - grid[i][j+1]
for x := i - 1; x <= i+1; x++ {
for y := j - 1; y <= j+1; y++ {
s += grid[x][y]
}
}
ans = max(ans, s)
}
}
return
}
func max(a, b int) int {
if a > b {
return a
}
return b
}function maxSum(grid: number[][]): number {
const m = grid.length;
const n = grid[0].length;
let ans = 0;
for (let i = 1; i < m - 1; ++i) {
for (let j = 1; j < n - 1; ++j) {
let s = -grid[i][j - 1] - grid[i][j + 1];
for (let x = i - 1; x <= i + 1; ++x) {
for (let y = j - 1; y <= j + 1; ++y) {
s += grid[x][y];
}
}
ans = Math.max(ans, s);
}
}
return ans;
}