README.md

2352. 相等行列对

English Version

题目描述

给你一个下标从 0 开始、大小为 n x n 的整数矩阵 grid ，返回满足 Ri 行和 Cj 列相等的行列对 (Ri, Cj) 的数目。

如果行和列以相同的顺序包含相同的元素（即相等的数组），则认为二者是相等的。

 

示例 1：

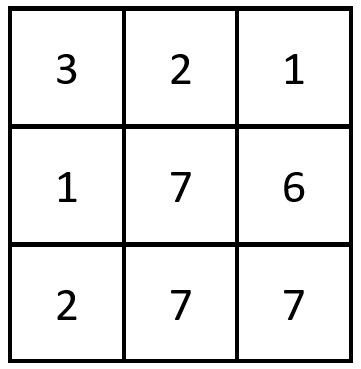
输入：grid = [[3,2,1],[1,7,6],[2,7,7]]
输出：1
解释：存在一对相等行列对：
- (第 2 行，第 1 列)：[2,7,7]

示例 2：

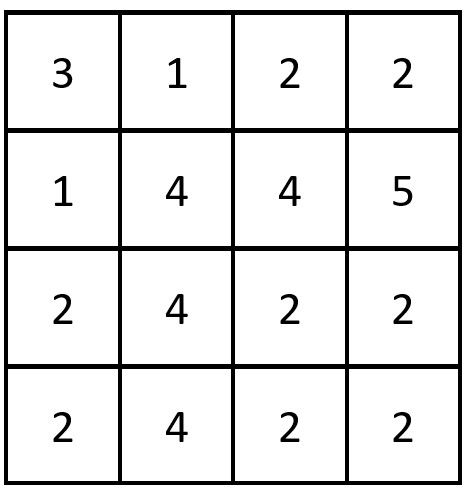
输入：grid = [[3,1,2,2],[1,4,4,5],[2,4,2,2],[2,4,2,2]]
输出：3
解释：存在三对相等行列对：
- (第 0 行，第 0 列)：[3,1,2,2]
- (第 2 行, 第 2 列)：[2,4,2,2]
- (第 3 行, 第 2 列)：[2,4,2,2]

 

提示：

• n == grid.length == grid[i].length
• 1 <= n <= 200
• 1 <= grid[i][j] <= 105

解法

方法一：模拟

将矩阵 grid 的每一行以及每一列进行比较，如果相等，那么就是一对相等行列对，答案加一。

时间复杂度 $O(n^3)$，空间复杂度 $O(1)$。其中 $n$ 为矩阵 grid 的行数或列数。

Python3

class Solution:
    def equalPairs(self, grid: List[List[int]]) -> int:
        g = [list(col) for col in zip(*grid)]
        return sum(row == col for row in grid for col in g)

class Solution:
    def equalPairs(self, grid: List[List[int]]) -> int:
        n = len(grid)
        ans = 0
        for i in range(n):
            for j in range(n):
                ans += all(grid[i][k] == grid[k][j] for k in range(n))
        return ans

Java

class Solution {
    public int equalPairs(int[][] grid) {
        int n = grid.length;
        int[][] g = new int[n][n];
        for (int j = 0; j < n; ++j) {
            for (int i = 0; i < n; ++i) {
                g[i][j] = grid[j][i];
            }
        }
        int ans = 0;
        for (var row : grid) {
            for (var col : g) {
                int ok = 1;
                for (int i = 0; i < n; ++i) {
                    if (row[i] != col[i]) {
                        ok = 0;
                        break;
                    }
                }
                ans += ok;
            }
        }
        return ans;
    }
}

class Solution {
    public int equalPairs(int[][] grid) {
        int n = grid.length;
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                int ok = 1;
                for (int k = 0; k < n; ++k) {
                    if (grid[i][k] != grid[k][j]) {
                        ok = 0;
                        break;
                    }
                }
                ans += ok;
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int equalPairs(vector<vector<int>>& grid) {
        int n = grid.size();
        vector<vector<int>> g(n, vector<int>(n));
        for (int j = 0; j < n; ++j) {
            for (int i = 0; i < n; ++i) {
                g[i][j] = grid[j][i];
            }
        }
        int ans = 0;
        for (auto& row : grid) {
            for (auto& col : g) {
                ans += row == col;
            }
        }
        return ans;
    }
};

class Solution {
public:
    int equalPairs(vector<vector<int>>& grid) {
        int n = grid.size();
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                int ok = 1;
                for (int k = 0; k < n; ++k) {
                    if (grid[i][k] != grid[k][j]) {
                        ok = 0;
                        break;
                    }
                }
                ans += ok;
            }
        }
        return ans;
    }
};

Go

func equalPairs(grid [][]int) (ans int) {
	n := len(grid)
	g := make([][]int, n)
	for i := range g {
		g[i] = make([]int, n)
		for j := 0; j < n; j++ {
			g[i][j] = grid[j][i]
		}
	}
	for _, row := range grid {
		for _, col := range g {
			ok := 1
			for i, v := range row {
				if v != col[i] {
					ok = 0
					break
				}
			}
			ans += ok
		}
	}
	return
}

func equalPairs(grid [][]int) (ans int) {
	for i := range grid {
		for j := range grid {
			ok := 1
			for k := range grid {
				if grid[i][k] != grid[k][j] {
					ok = 0
					break
				}
			}
			ans += ok
		}
	}
	return
}

TypeScript

...