README.md

2319. 判断矩阵是否是一个 X 矩阵

English Version

题目描述

如果一个正方形矩阵满足下述 全部 条件，则称之为一个 X 矩阵 ：

1. 矩阵对角线上的所有元素都 不是 0
2. 矩阵中所有其他元素都是 0

给你一个大小为 n x n 的二维整数数组 grid ，表示一个正方形矩阵。如果 grid 是一个 X 矩阵 ，返回 true ；否则，返回 false 。

 

示例 1：

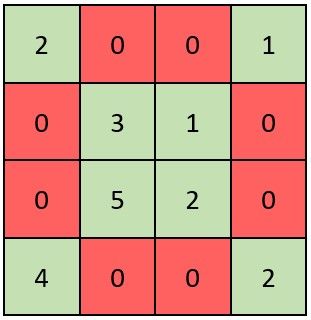
输入：grid = [[2,0,0,1],[0,3,1,0],[0,5,2,0],[4,0,0,2]]
输出：true
解释：矩阵如上图所示。
X 矩阵应该满足：绿色元素（对角线上）都不是 0 ，红色元素都是 0 。
因此，grid 是一个 X 矩阵。

示例 2：

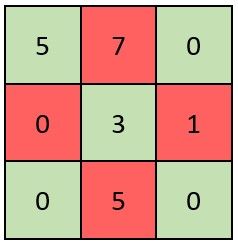
输入：grid = [[5,7,0],[0,3,1],[0,5,0]]
输出：false
解释：矩阵如上图所示。
X 矩阵应该满足：绿色元素（对角线上）都不是 0 ，红色元素都是 0 。
因此，grid 不是一个 X 矩阵。

 

提示：

• n == grid.length == grid[i].length
• 3 <= n <= 100
• 0 <= grid[i][j] <= 105

解法

方法一：模拟

遍历矩阵，对于每个元素，判断其是否满足 $X$ 矩阵的条件。若不满足，直接返回 false；若遍历完所有元素都满足，返回 true。

时间复杂度 $O(n^2)$，空间复杂度 $O(1)$。其中 $n$ 为矩阵的行数或列数。

Python3

class Solution:
    def checkXMatrix(self, grid: List[List[int]]) -> bool:
        for i, row in enumerate(grid):
            for j, v in enumerate(row):
                if i == j or i + j == len(grid) - 1:
                    if v == 0:
                        return False
                elif v:
                    return False
        return True

Java

class Solution {
    public boolean checkXMatrix(int[][] grid) {
        int n = grid.length;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == j || i + j == n - 1) {
                    if (grid[i][j] == 0) {
                        return false;
                    }
                } else if (grid[i][j] != 0) {
                    return false;
                }
            }
        }
        return true;
    }
}

C++

class Solution {
public:
    bool checkXMatrix(vector<vector<int>>& grid) {
        int n = grid.size();
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == j || i + j == n - 1) {
                    if (!grid[i][j]) {
                        return false;
                    }
                } else if (grid[i][j]) {
                    return false;
                }
            }
        }
        return true;
    }
};

Go

func checkXMatrix(grid [][]int) bool {
	for i, row := range grid {
		for j, v := range row {
			if i == j || i+j == len(row)-1 {
				if v == 0 {
					return false
				}
			} else if v != 0 {
				return false
			}
		}
	}
	return true
}

TypeScript

function checkXMatrix(grid: number[][]): boolean {
    const n = grid.length;
    for (let i = 0; i < n; ++i) {
        for (let j = 0; j < n; ++j) {
            if (i == j || i + j == n - 1) {
                if (!grid[i][j]) {
                    return false;
                }
            } else if (grid[i][j]) {
                return false;
            }
        }
    }
    return true;
}

C#

public class Solution {
    public bool CheckXMatrix(int[][] grid) {
        int n = grid.Length;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == j || i + j == n - 1) {
                    if (grid[i][j] == 0) {
                        return false;
                    }
                } else if (grid[i][j] != 0) {
                    return false;
                }
            }
        }
        return true;
    }
}

Rust

impl Solution {
    pub fn check_x_matrix(grid: Vec<Vec<i32>>) -> bool {
        let n = grid.len();
        for i in 0..n {
            for j in 0..n {
                if i == j || i + j == n - 1 {
                    if grid[i][j] == 0 {
                        return false;
                    }
                } else if grid[i][j] != 0 {
                    return false;
                }
            }
        }
        true
    }
}

C

bool checkXMatrix(int **grid, int gridSize, int *gridColSize) {
    for (int i = 0; i < gridSize; i++) {
        for (int j = 0; j < gridSize; j++) {
            if (i == j || i + j == gridSize - 1) {
                if (grid[i][j] == 0) {
                    return false;
                }
            } else if (grid[i][j] != 0) {
                return false;
            }
        }
    }
    return true;
}

...