README_EN.md

2093. Minimum Cost to Reach City With Discounts

中文文档

Description

A series of highways connect n cities numbered from 0 to n - 1. You are given a 2D integer array highways where highways[i] = [city1i, city2i, tolli] indicates that there is a highway that connects city1i and city2i, allowing a car to go from city1i to city2i and vice versa for a cost of tolli.

You are also given an integer discounts which represents the number of discounts you have. You can use a discount to travel across the ith highway for a cost of tolli / 2 (integer division). Each discount may only be used once, and you can only use at most one discount per highway.

Return the minimum total cost to go from city 0 to city n - 1, or -1 if it is not possible to go from city 0 to city n - 1.

 

Example 1:

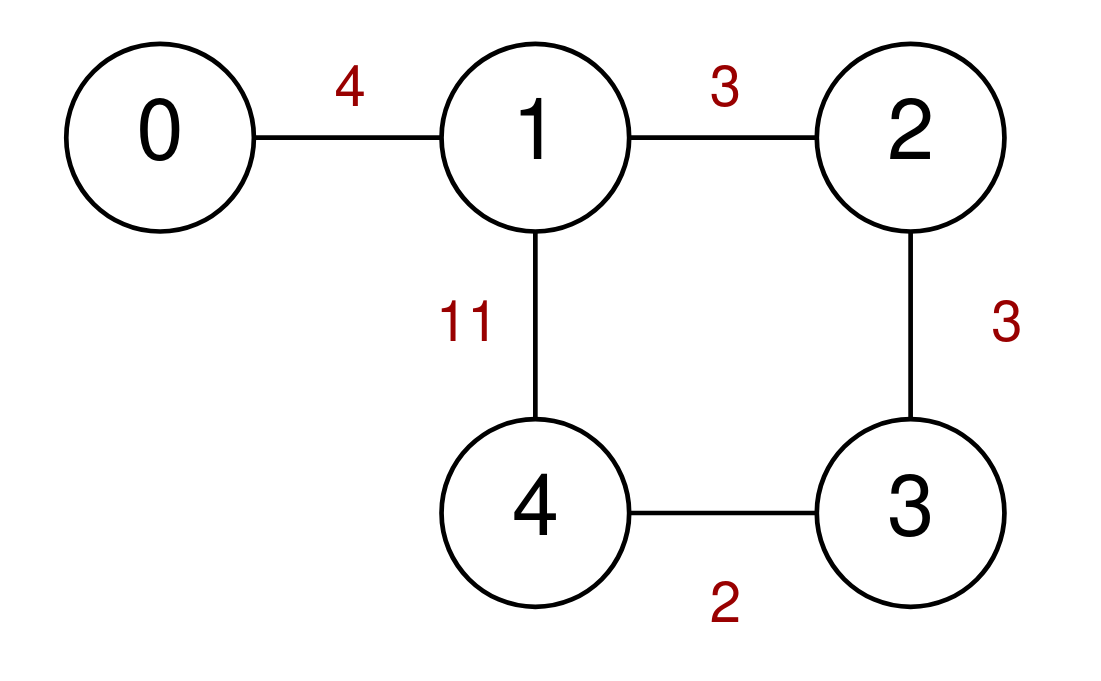
Input: n = 5, highways = [[0,1,4],[2,1,3],[1,4,11],[3,2,3],[3,4,2]], discounts = 1
Output: 9
Explanation:
Go from 0 to 1 for a cost of 4.
Go from 1 to 4 and use a discount for a cost of 11 / 2 = 5.
The minimum cost to go from 0 to 4 is 4 + 5 = 9.

Example 2:

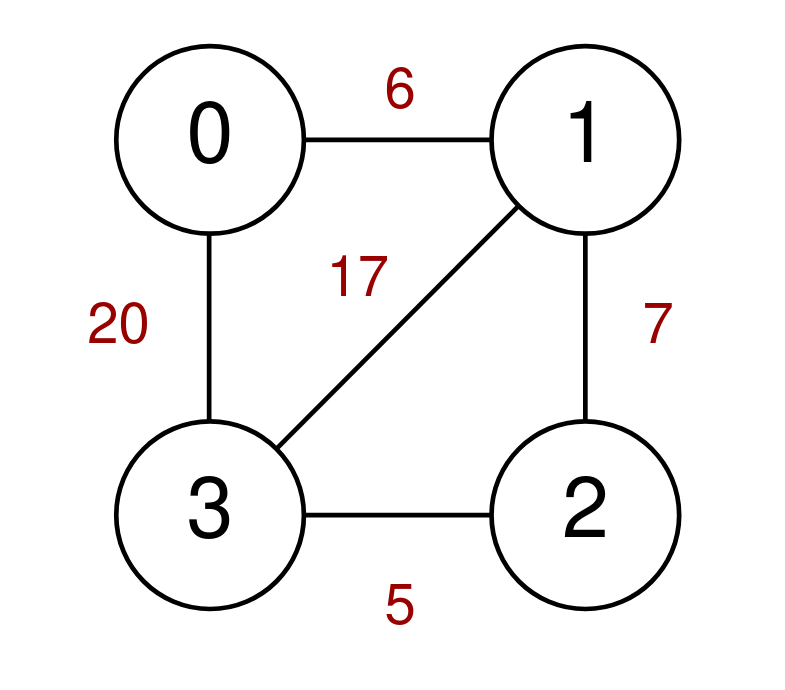
Input: n = 4, highways = [[1,3,17],[1,2,7],[3,2,5],[0,1,6],[3,0,20]], discounts = 20
Output: 8
Explanation:
Go from 0 to 1 and use a discount for a cost of 6 / 2 = 3.
Go from 1 to 2 and use a discount for a cost of 7 / 2 = 3.
Go from 2 to 3 and use a discount for a cost of 5 / 2 = 2.
The minimum cost to go from 0 to 3 is 3 + 3 + 2 = 8.

Example 3:

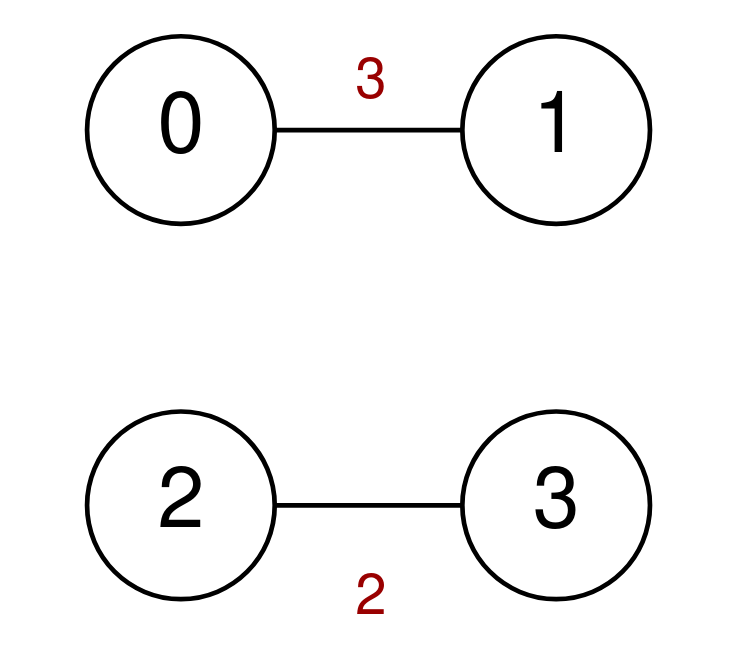
Input: n = 4, highways = [[0,1,3],[2,3,2]], discounts = 0
Output: -1
Explanation:
It is impossible to go from 0 to 3 so return -1.

 

Constraints:

• 2 <= n <= 1000
• 1 <= highways.length <= 1000
• highways[i].length == 3
• 0 <= city1i, city2i <= n - 1
• city1i != city2i
• 0 <= tolli <= 105
• 0 <= discounts <= 500
• There are no duplicate highways.

Solutions

Python3

class Solution:
    def minimumCost(self, n: int, highways: List[List[int]], discounts: int) -> int:
        g = defaultdict(list)
        for a, b, c in highways:
            g[a].append((b, c))
            g[b].append((a, c))
        q = [(0, 0, 0)]
        dist = [[inf] * (discounts + 1) for _ in range(n)]
        while q:
            cost, i, k = heappop(q)
            if k > discounts:
                continue
            if i == n - 1:
                return cost
            if dist[i][k] > cost:
                dist[i][k] = cost
                for j, v in g[i]:
                    heappush(q, (cost + v, j, k))
                    heappush(q, (cost + v // 2, j, k + 1))
        return -1

Java

class Solution {
    public int minimumCost(int n, int[][] highways, int discounts) {
        List<int[]>[] g = new List[n];
        for (int i = 0; i < n; ++i) {
            g[i] = new ArrayList<>();
        }
        for (var e : highways) {
            int a = e[0], b = e[1], c = e[2];
            g[a].add(new int[] {b, c});
            g[b].add(new int[] {a, c});
        }
        PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> a[0] - b[0]);
        q.offer(new int[] {0, 0, 0});
        int[][] dist = new int[n][discounts + 1];
        for (var e : dist) {
            Arrays.fill(e, Integer.MAX_VALUE);
        }
        while (!q.isEmpty()) {
            var p = q.poll();
            int cost = p[0], i = p[1], k = p[2];
            if (k > discounts || dist[i][k] <= cost) {
                continue;
            }
            if (i == n - 1) {
                return cost;
            }
            dist[i][k] = cost;
            for (int[] nxt : g[i]) {
                int j = nxt[0], v = nxt[1];
                q.offer(new int[] {cost + v, j, k});
                q.offer(new int[] {cost + v / 2, j, k + 1});
            }
        }
        return -1;
    }
}

C++

class Solution {
public:
    int minimumCost(int n, vector<vector<int>>& highways, int discounts) {
        vector<vector<pair<int, int>>> g(n);
        for (auto& e : highways) {
            int a = e[0], b = e[1], c = e[2];
            g[a].push_back({b, c});
            g[b].push_back({a, c});
        }
        priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, greater<tuple<int, int, int>>> q;
        q.push({0, 0, 0});
        vector<vector<int>> dist(n, vector<int>(discounts + 1, INT_MAX));
        while (!q.empty()) {
            auto [cost, i, k] = q.top();
            q.pop();
            if (k > discounts || dist[i][k] <= cost) continue;
            if (i == n - 1) return cost;
            dist[i][k] = cost;
            for (auto [j, v] : g[i]) {
                q.push({cost + v, j, k});
                q.push({cost + v / 2, j, k + 1});
            }
        }
        return -1;
    }
};

TypeScript

...