README.md

2033. 获取单值网格的最小操作数

English Version

题目描述

给你一个大小为 m x n 的二维整数网格 grid 和一个整数 x 。每一次操作，你可以对 grid 中的任一元素 加 x 或 减 x 。

单值网格 是全部元素都相等的网格。

返回使网格化为单值网格所需的 最小 操作数。如果不能，返回 -1 。

 

示例 1：

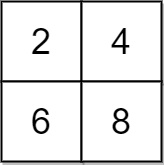
输入：grid = [[2,4],[6,8]], x = 2
输出：4
解释：可以执行下述操作使所有元素都等于 4 ： 
- 2 加 x 一次。
- 6 减 x 一次。
- 8 减 x 两次。
共计 4 次操作。

示例 2：

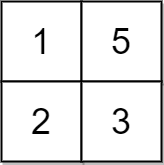
输入：grid = [[1,5],[2,3]], x = 1
输出：5
解释：可以使所有元素都等于 3 。

示例 3：

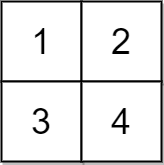
输入：grid = [[1,2],[3,4]], x = 2
输出：-1
解释：无法使所有元素相等。

 

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• 1 <= x, grid[i][j] <= 104

解法

方法一：贪心

首先，要使得网格化为单值网格，那么网格的所有元素与 $x$ 的余数必须相同。

因此，我们可以先遍历网格，判断所有元素与 $x$ 的余数是否相同，若不同则返回 $-1$。否则，我们将所有元素放入数组中，对数组进行排序，取中位数，然后遍历数组，计算每个元素与中位数的差值，再除以 $x$，将所有的差值相加，即为答案。

时间复杂度 $O((m \times n) \times \log (m \times n))$，空间复杂度 $O(m \times n)$。其中 $m$ 和 $n$ 分别为网格的行数和列数。

Python3

class Solution:
    def minOperations(self, grid: List[List[int]], x: int) -> int:
        nums = []
        mod = grid[0][0] % x
        for row in grid:
            for v in row:
                if v % x != mod:
                    return -1
                nums.append(v)
        nums.sort()
        mid = nums[len(nums) >> 1]
        return sum(abs(v - mid) // x for v in nums)

Java

class Solution {
    public int minOperations(int[][] grid, int x) {
        int m = grid.length, n = grid[0].length;
        int[] nums = new int[m * n];
        int mod = grid[0][0] % x;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] % x != mod) {
                    return -1;
                }
                nums[i * n + j] = grid[i][j];
            }
        }
        Arrays.sort(nums);
        int mid = nums[nums.length >> 1];
        int ans = 0;
        for (int v : nums) {
            ans += Math.abs(v - mid) / x;
        }
        return ans;
    }
}

C++

class Solution {
public:
    int minOperations(vector<vector<int>>& grid, int x) {
        int m = grid.size(), n = grid[0].size();
        int mod = grid[0][0] % x;
        int nums[m * n];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] % x != mod) {
                    return -1;
                }
                nums[i * n + j] = grid[i][j];
            }
        }
        sort(nums, nums + m * n);
        int mid = nums[(m * n) >> 1];
        int ans = 0;
        for (int v : nums) {
            ans += abs(v - mid) / x;
        }
        return ans;
    }
};

Go

func minOperations(grid [][]int, x int) int {
	mod := grid[0][0] % x
	nums := []int{}
	for _, row := range grid {
		for _, v := range row {
			if v%x != mod {
				return -1
			}
			nums = append(nums, v)
		}
	}
	sort.Ints(nums)
	mid := nums[len(nums)>>1]
	ans := 0
	for _, v := range nums {
		ans += abs(v-mid) / x
	}
	return ans
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}

...