有一个立方体房间,其长度、宽度和高度都等于 n 个单位。请你在房间里放置 n 个盒子,每个盒子都是一个单位边长的立方体。放置规则如下:
- 你可以把盒子放在地板上的任何地方。
- 如果盒子
x需要放置在盒子y的顶部,那么盒子y竖直的四个侧面都 必须 与另一个盒子或墙相邻。
给你一个整数 n ,返回接触地面的盒子的 最少 可能数量。
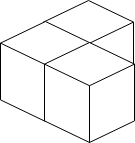
示例 1:
输入:n = 3 输出:3 解释:上图是 3 个盒子的摆放位置。 这些盒子放在房间的一角,对应左侧位置。
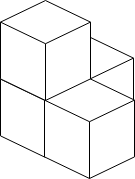
示例 2:
输入:n = 4 输出:3 解释:上图是 3 个盒子的摆放位置。 这些盒子放在房间的一角,对应左侧位置。
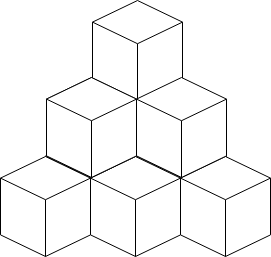
示例 3:
输入:n = 10 输出:6 解释:上图是 10 个盒子的摆放位置。 这些盒子放在房间的一角,对应后方位置。
提示:
1 <= n <= 109
方法一:数学规律
根据题目描述,层数最高的盒子需要放在墙角,并且盒子的摆放呈阶梯状,这样可以使得接触地面的盒子数量最少。
假设盒子摆放
如果此时盒子还有剩余,那么可以从最低一层继续摆放,假设摆放
时间复杂度
class Solution:
def minimumBoxes(self, n: int) -> int:
s, k = 0, 1
while s + k * (k + 1) // 2 <= n:
s += k * (k + 1) // 2
k += 1
k -= 1
ans = k * (k + 1) // 2
k = 1
while s < n:
ans += 1
s += k
k += 1
return ansclass Solution {
public int minimumBoxes(int n) {
int s = 0, k = 1;
while (s + k * (k + 1) / 2 <= n) {
s += k * (k + 1) / 2;
++k;
}
--k;
int ans = k * (k + 1) / 2;
k = 1;
while (s < n) {
++ans;
s += k;
++k;
}
return ans;
}
}class Solution {
public:
int minimumBoxes(int n) {
int s = 0, k = 1;
while (s + k * (k + 1) / 2 <= n) {
s += k * (k + 1) / 2;
++k;
}
--k;
int ans = k * (k + 1) / 2;
k = 1;
while (s < n) {
++ans;
s += k;
++k;
}
return ans;
}
};func minimumBoxes(n int) int {
s, k := 0, 1
for s+k*(k+1)/2 <= n {
s += k * (k + 1) / 2
k++
}
k--
ans := k * (k + 1) / 2
k = 1
for s < n {
ans++
s += k
k++
}
return ans
}