你有一棵二叉树,这棵二叉树有个小问题,其中有且只有一个无效节点,它的右子节点错误地指向了与其在同一层且在其右侧的一个其他节点。
给定一棵这样的问题二叉树的根节点 root ,将该无效节点及其所有子节点移除(除被错误指向的节点外),然后返回新二叉树的根结点。
自定义测试用例:
测试用例的输入由三行组成:
TreeNode rootint fromNode(在correctBinaryTree中不可见)int toNode(在correctBinaryTree中不可见)
当以 root 为根的二叉树被解析后,值为 fromNode 的节点 TreeNode 将其右子节点指向值为 toNode 的节点 TreeNode 。然后, root 传入 correctBinaryTree 的参数中。
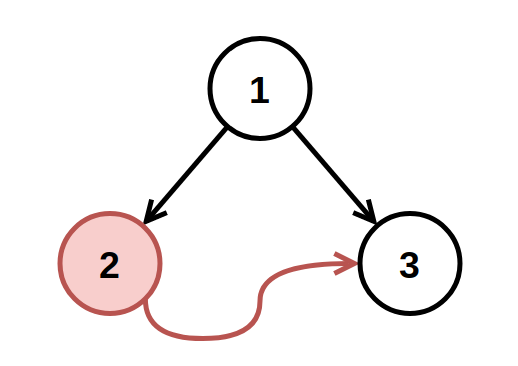
示例 1:
输入: root = [1,2,3], fromNode = 2, toNode = 3 输出: [1,null,3] 解释: 值为 2 的节点是无效的,所以移除之。
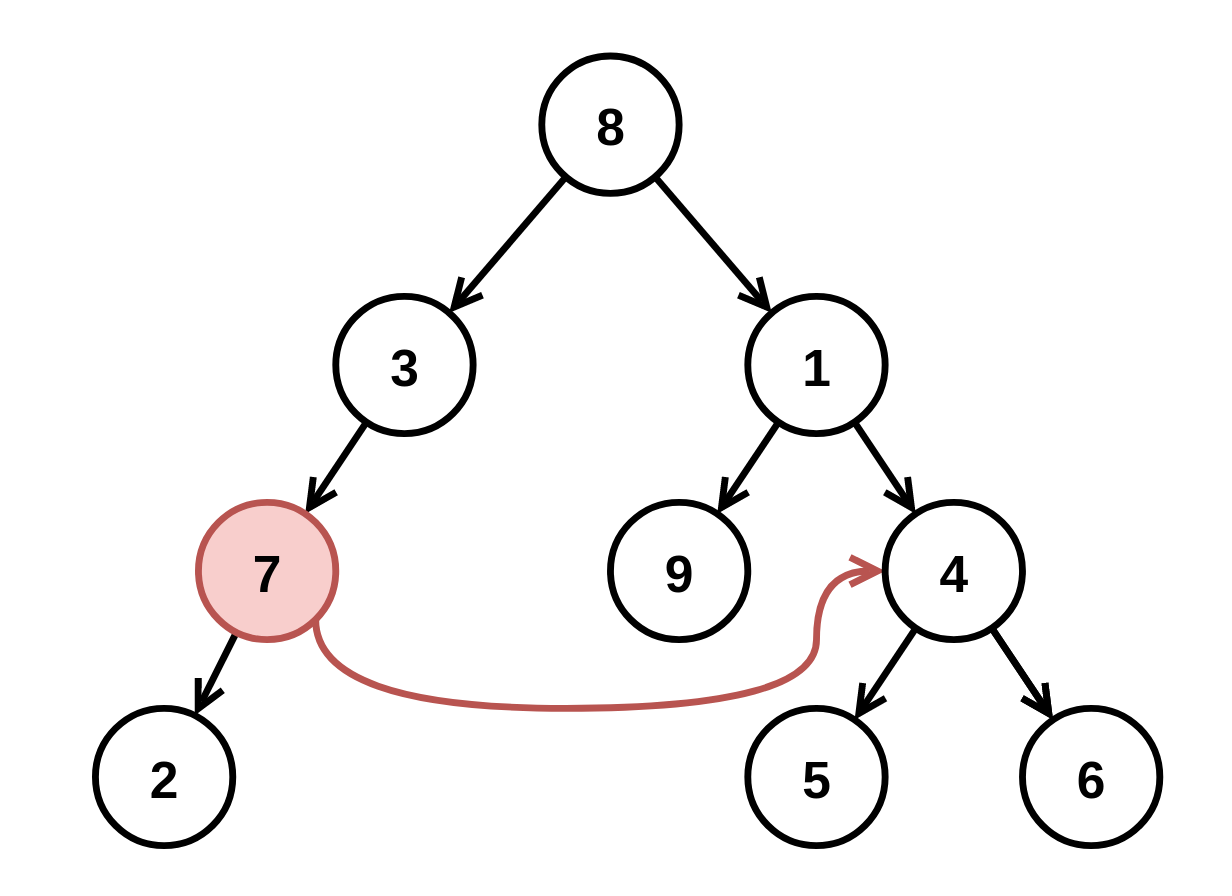
示例 2:
输入: root = [8,3,1,7,null,9,4,2,null,null,null,5,6], fromNode = 7, toNode = 4 输出: [8,3,1,null,null,9,4,null,null,5,6] 解释: 值为 7 的节点是无效的,所以移除这个节点及其子节点 2。
提示:
- 树中节点个数的范围是
[3, 104]。 -109 <= Node.val <= 109- 所有的
Node.val都是互不相同的。 fromNode != toNodefromNode和toNode将出现在树中的同一层。toNode在fromNode的右侧。fromNode.right在测试用例的树中建立后为null。
方法一:DFS
我们设计一个函数
最后,返回
时间复杂度
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def correctBinaryTree(self, root: TreeNode) -> TreeNode:
def dfs(root):
if root is None or root.right in vis:
return None
vis.add(root)
root.right = dfs(root.right)
root.left = dfs(root.left)
return root
vis = set()
return dfs(root)/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private Set<TreeNode> vis = new HashSet<>();
public TreeNode correctBinaryTree(TreeNode root) {
return dfs(root);
}
private TreeNode dfs(TreeNode root) {
if (root == null || vis.contains(root.right)) {
return null;
}
vis.add(root);
root.right = dfs(root.right);
root.left = dfs(root.left);
return root;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* correctBinaryTree(TreeNode* root) {
unordered_set<TreeNode*> vis;
function<TreeNode*(TreeNode*)> dfs = [&](TreeNode* root) -> TreeNode* {
if (!root || vis.count(root->right)) {
return nullptr;
}
vis.insert(root);
root->right = dfs(root->right);
root->left = dfs(root->left);
return root;
};
return dfs(root);
}
};/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} from
* @param {number} to
* @return {TreeNode}
*/
var correctBinaryTree = function (root) {
const dfs = root => {
if (!root || vis.has(root.right)) {
return null;
}
vis.add(root);
root.right = dfs(root.right);
root.left = dfs(root.left);
return root;
};
const vis = new Set();
return dfs(root);
};