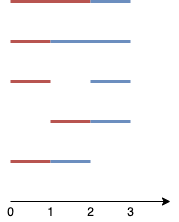Skip to content

Latest commit

 

History

History
234 lines (185 loc) · 6.61 KB

README.md

File metadata and controls

234 lines (185 loc) · 6.61 KB
Raw

1621. 大小为 K 的不重叠线段的数目

English Version

题目描述

给你一维空间的 n 个点，其中第 i 个点（编号从 0 到 n-1）位于 x = i 处，请你找到 恰好 k 个不重叠 线段且每个线段至少覆盖两个点的方案数。线段的两个端点必须都是 整数坐标 。这 k 个线段不需要全部覆盖全部 n 个点，且它们的端点 可以 重合。

请你返回 k 个不重叠线段的方案数。由于答案可能很大，请将结果对 109 + 7 取余 后返回。

 

示例 1：

输入：n = 4, k = 2
输出：5
解释：
如图所示，两个线段分别用红色和蓝色标出。
上图展示了 5 种不同的方案 {(0,2),(2,3)}，{(0,1),(1,3)}，{(0,1),(2,3)}，{(1,2),(2,3)}，{(0,1),(1,2)} 。

示例 2：

输入：n = 3, k = 1
输出：3
解释：总共有 3 种不同的方案 {(0,1)}, {(0,2)}, {(1,2)} 。

示例 3：

输入：n = 30, k = 7
输出：796297179
解释：画 7 条线段的总方案数为 3796297200 种。将这个数对 109 + 7 取余得到 796297179 。

示例 4：

输入：n = 5, k = 3
输出：7

示例 5：

输入：n = 3, k = 2
输出：1

 

提示：

  • 2 <= n <= 1000
  • 1 <= k <= n-1

解法

方法一：动态规划

记 $f[i][j]$ 表示使用前 $i$ 个点构造了 $j$ 条线段，且最后一条线段的右端点不为 $i$ 的方案数；记 $g[i][j]$ 表示使用了前 $i$ 个点构造了 $j$ 条线段，且最后一条线段的右端点为 $i$ 的方案数。初始时 $f[1][0]=1$。

考虑 $f[i][j]$，由于第 $j$ 条线段的右端点不为 $i$，因此前 $i-1$ 个点构造了 $j$ 条线段，因此有：

$$ f[i][j] = f[i-1][j] + g[i - 1][j] $$

考虑 $g[i][j]$，第 $j$ 条线段的右端点为 $i$，如果第 $j$ 条线段的长度超过 $1$，则前 $i-1$ 个点构造了 $j$ 条线段，且第 $j$ 条线段的右端点一定覆盖了 $i-1$，因此有：

$$ g[i][j] = g[i - 1][j] $$

如果第 $j$ 条线段的长度为 $1$，则前 $i-1$ 个点构造了 $j-1$ 条线段，有：

$$ g[i][j] = f[i - 1][j - 1] + g[i - 1][j - 1] $$

答案为 $f[n][k]+g[n][k]$。

时间复杂度 $O(n\times k)$，空间复杂度 $O(n\times k)$。

Python3

class Solution:
    def numberOfSets(self, n: int, k: int) -> int:
        mod = 10**9 + 7
        f = [[0] * (k + 1) for _ in range(n + 1)]
        g = [[0] * (k + 1) for _ in range(n + 1)]
        f[1][0] = 1
        for i in range(2, n + 1):
            for j in range(k + 1):
                f[i][j] = (f[i - 1][j] + g[i - 1][j]) % mod
                g[i][j] = g[i - 1][j]
                if j:
                    g[i][j] += f[i - 1][j - 1]
                    g[i][j] %= mod
                    g[i][j] += g[i - 1][j - 1]
                    g[i][j] %= mod
        return (f[-1][-1] + g[-1][-1]) % mod

Java

class Solution {
    private static final int MOD = (int) 1e9 + 7;

    public int numberOfSets(int n, int k) {
        int[][] f = new int[n + 1][k + 1];
        int[][] g = new int[n + 1][k + 1];
        f[1][0] = 1;
        for (int i = 2; i <= n; ++i) {
            for (int j = 0; j <= k; ++j) {
                f[i][j] = (f[i - 1][j] + g[i - 1][j]) % MOD;
                g[i][j] = g[i - 1][j];
                if (j > 0) {
                    g[i][j] += f[i - 1][j - 1];
                    g[i][j] %= MOD;
                    g[i][j] += g[i - 1][j - 1];
                    g[i][j] %= MOD;
                }
            }
        }
        return (f[n][k] + g[n][k]) % MOD;
    }
}

C++

class Solution {
public:
    int f[1010][1010];
    int g[1010][1010];
    const int mod = 1e9 + 7;

    int numberOfSets(int n, int k) {
        memset(f, 0, sizeof(f));
        memset(g, 0, sizeof(g));
        f[1][0] = 1;
        for (int i = 2; i <= n; ++i) {
            for (int j = 0; j <= k; ++j) {
                f[i][j] = (f[i - 1][j] + g[i - 1][j]) % mod;
                g[i][j] = g[i - 1][j];
                if (j > 0) {
                    g[i][j] += f[i - 1][j - 1];
                    g[i][j] %= mod;
                    g[i][j] += g[i - 1][j - 1];
                    g[i][j] %= mod;
                }
            }
        }
        return (f[n][k] + g[n][k]) % mod;
    }
};

Go

func numberOfSets(n int, k int) int {
	f := make([][]int, n+1)
	g := make([][]int, n+1)
	for i := range f {
		f[i] = make([]int, k+1)
		g[i] = make([]int, k+1)
	}
	f[1][0] = 1
	var mod int = 1e9 + 7
	for i := 2; i <= n; i++ {
		for j := 0; j <= k; j++ {
			f[i][j] = (f[i-1][j] + g[i-1][j]) % mod
			g[i][j] = g[i-1][j]
			if j > 0 {
				g[i][j] += f[i-1][j-1]
				g[i][j] %= mod
				g[i][j] += g[i-1][j-1]
				g[i][j] %= mod
			}
		}
	}
	return (f[n][k] + g[n][k]) % mod
}

TypeScript

function numberOfSets(n: number, k: number): number {
    const f = Array.from({ length: n + 1 }, _ => new Array(k + 1).fill(0));
    const g = Array.from({ length: n + 1 }, _ => new Array(k + 1).fill(0));
    f[1][0] = 1;
    const mod = 10 ** 9 + 7;
    for (let i = 2; i <= n; ++i) {
        for (let j = 0; j <= k; ++j) {
            f[i][j] = (f[i - 1][j] + g[i - 1][j]) % mod;
            g[i][j] = g[i - 1][j];
            if (j) {
                g[i][j] += f[i - 1][j - 1];
                g[i][j] %= mod;
                g[i][j] += g[i - 1][j - 1];
                g[i][j] %= mod;
            }
        }
    }
    return (f[n][k] + g[n][k]) % mod;
}

...