Skip to content

Latest commit

 

History

History
261 lines (199 loc) · 7.05 KB

README.md

File metadata and controls

261 lines (199 loc) · 7.05 KB

1506. 找到 N 叉树的根节点

English Version

题目描述

给定一棵 N 叉树 的所有节点在一个数组  Node[] tree 中，树中每个节点都有 唯一的值 。

找到并返回 N 叉树的 根节点 。

 

自定义测试：

N 叉树的输入序列为其层序遍历序列，每组子节点用 null 分隔（见示例）。

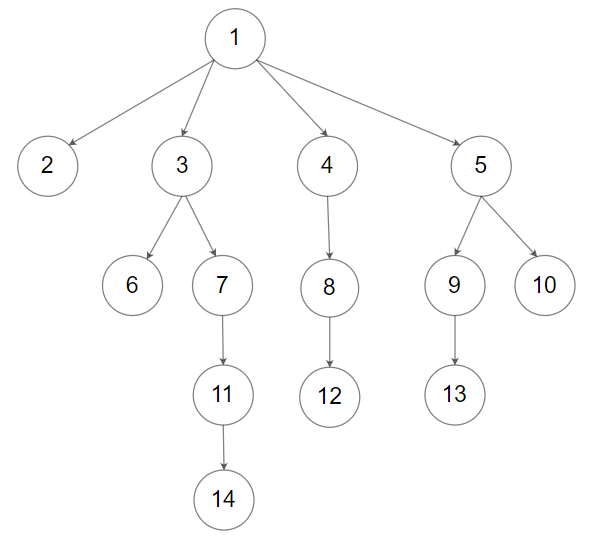
上图中的 N 叉树的序列化描述为 [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] 。

测试将以下列方式进行：

  • 输入数据的形式为树的序列化描述。
  • 驱动程序代码将根据序列化的输入数据构造树，并以任意顺序将每个 Node 对象放入一个数组中。
  • 驱动程序代码将把数组传递给 findRoot ，你所编写的函数应该在数组中查找并返回根 Node 对象。
  • 驱动程序代码将接受返回的 Node 对象并对其进行序列化。如果序列化的结果和输入数据 相同 ，则测试 通过 。

 

示例 1：

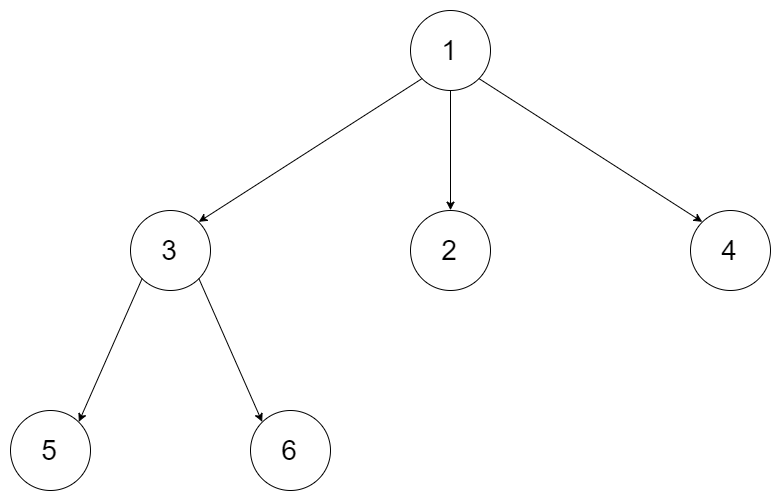
输入：tree = [1,null,3,2,4,null,5,6]
输出：[1,null,3,2,4,null,5,6]
解释：来自输入数据的树如上所示。
驱动程序代码创建树，并以任意顺序向 findRoot 提供 Node 对象。
例如，传递的数组可以是 [Node(5),Node(4),Node(3),Node(6),Node(2),Node(1)] 或 [Node(2),Node(6),Node(1),Node(3),Node(5),Node(4)] 。
findRoot 函数应该返回根 Node(1) ，驱动程序代码将序列化它并与输入数据进行比较。
输入数据和序列化的 Node(1) 相同，因此测试通过。

示例 2：

输入：tree = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]

 

提示：

  • 节点的总个数在 [1, 5*10^4] 之间。
  • 每个节点都有唯一的值。

 

进阶：

  • 你可以使用 O(1) 额外内存空间且 O(n) 时间复杂度的算法来找到该树的根节点吗？

解法

方法一：位运算

对于一棵 N 叉树的节点，如果该节点是根节点，那么该节点只会出现一次在数组 tree 中；而如果该节点不是根节点，那么该节点会出现两次，一次在数组 tree 中，一次在该节点的父节点的 children 数组中。

因此，我们可以遍历数组 tree，计算每个节点的值以及其所有子节点的值的异或和，记录在变量 $x$ 中。遍历结束后，我们得到的 $x$ 就是根节点的值。

接下来，我们再遍历数组 tree，找到值为 $x$ 的节点，即为根节点，返回即可。

时间复杂度 $O(n)$，空间复杂度 $O(1)$。其中 $n$ 为数组 tree 的长度。

Python3

"""
# Definition for a Node.
class Node:
    def __init__(self, val=None, children=None):
        self.val = val
        self.children = children if children is not None else []
"""


class Solution:
    def findRoot(self, tree: List['Node']) -> 'Node':
        x = 0
        for node in tree:
            x ^= node.val
            for child in node.children:
                x ^= child.val
        return next(node for node in tree if node.val == x)

Java

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;


    public Node() {
        children = new ArrayList<Node>();
    }

    public Node(int _val) {
        val = _val;
        children = new ArrayList<Node>();
    }

    public Node(int _val,ArrayList<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
    public Node findRoot(List<Node> tree) {
        int x = 0;
        for (Node node : tree) {
            x ^= node.val;
            for (Node child : node.children) {
                x ^= child.val;
            }
        }
        for (int i = 0;; ++i) {
            if (tree.get(i).val == x) {
                return tree.get(i);
            }
        }
    }
}

C++

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    Node* findRoot(vector<Node*> tree) {
        int x = 0;
        for (Node* node : tree) {
            x ^= node->val;
            for (Node* child : node->children) {
                x ^= child->val;
            }
        }
        for (int i = 0;; ++i) {
            if (tree[i]->val == x) {
                return tree[i];
            }
        }
    }
};

Go

/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Children []*Node
 * }
 */

func findRoot(tree []*Node) *Node {
	x := 0
	for _, node := range tree {
		x ^= node.Val
		for _, child := range node.Children {
			x ^= child.Val
		}
	}
	for i := 0; ; i++ {
		if tree[i].Val == x {
			return tree[i]
		}
	}
}

TypeScript

/**
 * Definition for Node.
 * class Node {
 *     val: number
 *     children: Node[]
 *     constructor(val?: number, children?: Node[]) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.children = (children===undefined ? [] : children)
 *     }
 * }
 */

function findRoot(tree: Node[]): Node | null {
    let x = 0;
    for (const node of tree) {
        x ^= node.val;
        for (const child of node.children) {
            x ^= child.val;
        }
    }
    return tree.find(node => node.val === x) || null;
}

...