Skip to content

Latest commit

 

History

History
427 lines (365 loc) · 12.2 KB

README.md

File metadata and controls

427 lines (365 loc) · 12.2 KB
Raw

998. 最大二叉树 II

English Version

题目描述

最大树 定义：一棵树，并满足：其中每个节点的值都大于其子树中的任何其他值。

给你最大树的根节点 root 和一个整数 val 。

就像 之前的问题 那样，给定的树是利用 Construct(a) 例程从列表 a（root = Construct(a)）递归地构建的：

  • 如果 a 为空，返回 null 。
  • 否则，令 a[i] 作为 a 的最大元素。创建一个值为 a[i] 的根节点 root 。
  • root 的左子树将被构建为 Construct([a[0], a[1], ..., a[i - 1]]) 。
  • root 的右子树将被构建为 Construct([a[i + 1], a[i + 2], ..., a[a.length - 1]]) 。
  • 返回 root 。

请注意，题目没有直接给出 a ，只是给出一个根节点 root = Construct(a) 。

假设 b 是 a 的副本，并在末尾附加值 val。题目数据保证 b 中的值互不相同。

返回 Construct(b) 。

 

示例 1：

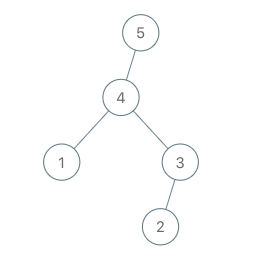
输入：root = [4,1,3,null,null,2], val = 5
输出：[5,4,null,1,3,null,null,2]
解释：a = [1,4,2,3], b = [1,4,2,3,5]

示例 2：

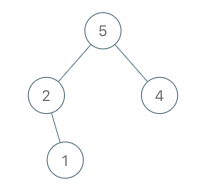
输入：root = [5,2,4,null,1], val = 3
输出：[5,2,4,null,1,null,3]
解释：a = [2,1,5,4], b = [2,1,5,4,3]

示例 3：

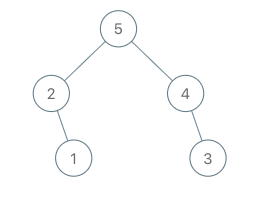
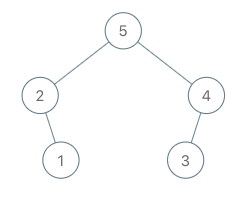
输入：root = [5,2,3,null,1], val = 4
输出：[5,2,4,null,1,3]
解释：a = [2,1,5,3], b = [2,1,5,3,4]

 

提示：

  • 树中节点数目在范围 [1, 100] 内
  • 1 <= Node.val <= 100
  • 树中的所有值 互不相同
  • 1 <= val <= 100

 

解法

方法一：递归

如果 $val$ 是最大数，那么将 $val$ 作为新的根节点，$root$ 作为新的根节点的左子树。

如果 $val$ 不是最大数，由于 $val$ 是在最后追加的数，那么一定是在 $root$ 的右边，所以将 $val$ 作为新节点插入 $root$ 的右子树即可。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。

方法二：迭代

搜索右子树，找到 $curr.val &gt; val &gt; curr.right.val$ 的节点，然后创建新的节点 $node$，把 $node.left$ 指向 $curr.right$，然后 $curr.right$ 指向 $node$。

最后返回 $root$。

时间复杂度 $O(n)$，空间复杂度 $O(1)$。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def insertIntoMaxTree(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
        if root is None or root.val < val:
            return TreeNode(val, root)
        root.right = self.insertIntoMaxTree(root.right, val)
        return root
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def insertIntoMaxTree(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
        if root.val < val:
            return TreeNode(val, root)
        curr = root
        node = TreeNode(val)
        while curr.right and curr.right.val > val:
            curr = curr.right
        node.left = curr.right
        curr.right = node
        return root

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode insertIntoMaxTree(TreeNode root, int val) {
        if (root == null || root.val < val) {
            return new TreeNode(val, root, null);
        }
        root.right = insertIntoMaxTree(root.right, val);
        return root;
    }
}
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode insertIntoMaxTree(TreeNode root, int val) {
        if (root.val < val) {
            return new TreeNode(val, root, null);
        }
        TreeNode curr = root;
        TreeNode node = new TreeNode(val);
        while (curr.right != null && curr.right.val > val) {
            curr = curr.right;
        }
        node.left = curr.right;
        curr.right = node;
        return root;
    }
}

TypeScript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function insertIntoMaxTree(
    root: TreeNode | null,
    val: number,
): TreeNode | null {
    if (!root || root.val < val) {
        return new TreeNode(val, root);
    }
    root.right = insertIntoMaxTree(root.right, val);
    return root;
}
/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function insertIntoMaxTree(
    root: TreeNode | null,
    val: number,
): TreeNode | null {
    if (root.val < val) {
        return new TreeNode(val, root);
    }
    const node = new TreeNode(val);
    let curr = root;
    while (curr.right && curr.right.val > val) {
        curr = curr.right;
    }
    node.left = curr.right;
    curr.right = node;
    return root;
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* insertIntoMaxTree(TreeNode* root, int val) {
        if (!root || root->val < val) return new TreeNode(val, root, nullptr);
        root->right = insertIntoMaxTree(root->right, val);
        return root;
    }
};
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* insertIntoMaxTree(TreeNode* root, int val) {
        if (root->val < val) return new TreeNode(val, root, nullptr);
        TreeNode* curr = root;
        TreeNode* node = new TreeNode(val);
        while (curr->right && curr->right->val > val) curr = curr->right;
        node->left = curr->right;
        curr->right = node;
        return root;
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func insertIntoMaxTree(root *TreeNode, val int) *TreeNode {
	if root == nil || root.Val < val {
		return &TreeNode{val, root, nil}
	}
	root.Right = insertIntoMaxTree(root.Right, val)
	return root
}
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func insertIntoMaxTree(root *TreeNode, val int) *TreeNode {
	if root.Val < val {
		return &TreeNode{val, root, nil}
	}
	node := &TreeNode{Val: val}
	curr := root
	for curr.Right != nil && curr.Right.Val > val {
		curr = curr.Right
	}
	node.Left = curr.Right
	curr.Right = node
	return root
}

C

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


struct TreeNode *insertIntoMaxTree(struct TreeNode *root, int val) {
    if (!root || root->val < val) {
        struct TreeNode *res = (struct TreeNode *) malloc(sizeof(struct TreeNode));
        res->val = val;
        res->left = root;
        res->right = NULL;
        return res;
    }
    root->right = insertIntoMaxTree(root->right, val);
    return root;
}

Rust

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    pub fn insert_into_max_tree(
        mut root: Option<Rc<RefCell<TreeNode>>>,
        val: i32,
    ) -> Option<Rc<RefCell<TreeNode>>> {
        if root.is_none() || root.as_ref().unwrap().as_ref().borrow().val < val {
            return Some(Rc::new(RefCell::new(TreeNode {
                val,
                left: root.take(),
                right: None,
            })));
        }
        {
            let mut root = root.as_ref().unwrap().as_ref().borrow_mut();
            root.right = Self::insert_into_max_tree(root.right.take(), val);
        }
        root
    }
}

...