README_EN.md

668. Kth Smallest Number in Multiplication Table

中文文档

Description

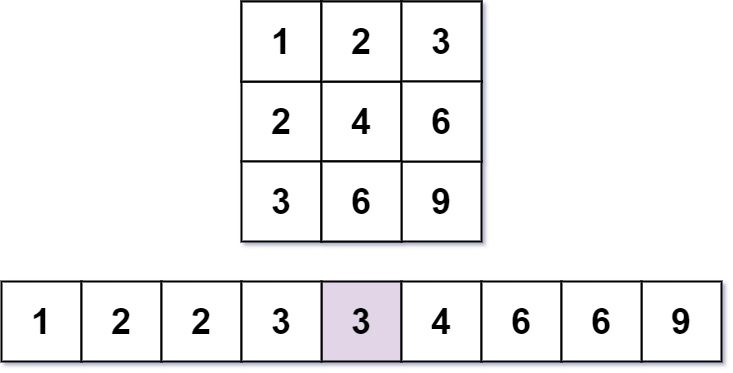
Nearly everyone has used the Multiplication Table. The multiplication table of size m x n is an integer matrix mat where mat[i][j] == i * j (1-indexed).

Given three integers m, n, and k, return the kth smallest element in the m x n multiplication table.

 

Example 1:

Input: m = 3, n = 3, k = 5
Output: 3
Explanation: The 5th smallest number is 3.

Example 2:

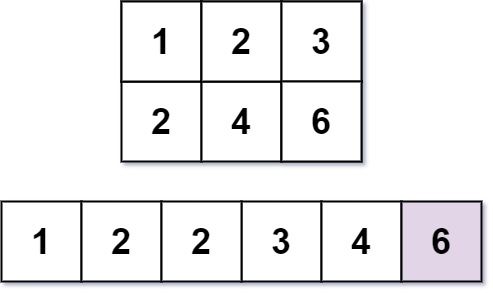
Input: m = 2, n = 3, k = 6
Output: 6
Explanation: The 6th smallest number is 6.

 

Constraints:

• 1 <= m, n <= 3 * 104
• 1 <= k <= m * n

Solutions

Binary search.

Python3

class Solution:
    def findKthNumber(self, m: int, n: int, k: int) -> int:
        left, right = 1, m * n
        while left < right:
            mid = (left + right) >> 1
            cnt = 0
            for i in range(1, m + 1):
                cnt += min(mid // i, n)
            if cnt >= k:
                right = mid
            else:
                left = mid + 1
        return left

Java

class Solution {
    public int findKthNumber(int m, int n, int k) {
        int left = 1, right = m * n;
        while (left < right) {
            int mid = (left + right) >>> 1;
            int cnt = 0;
            for (int i = 1; i <= m; ++i) {
                cnt += Math.min(mid / i, n);
            }
            if (cnt >= k) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }
}

C++

class Solution {
public:
    int findKthNumber(int m, int n, int k) {
        int left = 1, right = m * n;
        while (left < right) {
            int mid = (left + right) >> 1;
            int cnt = 0;
            for (int i = 1; i <= m; ++i) cnt += min(mid / i, n);
            if (cnt >= k)
                right = mid;
            else
                left = mid + 1;
        }
        return left;
    }
};

Go

func findKthNumber(m int, n int, k int) int {
	left, right := 1, m*n
	for left < right {
		mid := (left + right) >> 1
		cnt := 0
		for i := 1; i <= m; i++ {
			cnt += min(mid/i, n)
		}
		if cnt >= k {
			right = mid
		} else {
			left = mid + 1
		}
	}
	return left
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

...