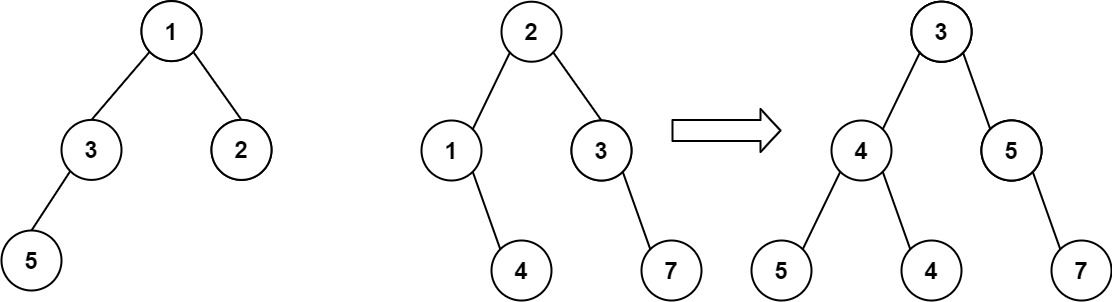
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1:
输入:root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7] 输出:[3,4,5,5,4,null,7]
示例 2:
输入:root1 = [1], root2 = [1,2] 输出:[2,2]
提示:
- 两棵树中的节点数目在范围
[0, 2000]内 -104 <= Node.val <= 104
方法一:递归
递归合并两棵树的节点。
- 如果其中一棵树的当前节点为空,则返回另一棵树的当前节点作为合并后节点。
- 如果两棵树的当前节点都不为空,则将它们的值相加作为合并后节点的新值,然后递归合并它们的左右子节点。
时间复杂度
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
if root1 is None:
return root2
if root2 is None:
return root1
node = TreeNode(root1.val + root2.val)
node.left = self.mergeTrees(root1.left, root2.left)
node.right = self.mergeTrees(root1.right, root2.right)
return node/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
if (root1 == null) {
return root2;
}
if (root2 == null) {
return root1;
}
TreeNode node = new TreeNode(root1.val + root2.val);
node.left = mergeTrees(root1.left, root2.left);
node.right = mergeTrees(root1.right, root2.right);
return node;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if (!root1) return root2;
if (!root2) return root1;
TreeNode* node = new TreeNode(root1->val + root2->val);
node->left = mergeTrees(root1->left, root2->left);
node->right = mergeTrees(root1->right, root2->right);
return node;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func mergeTrees(root1 *TreeNode, root2 *TreeNode) *TreeNode {
if root1 == nil {
return root2
}
if root2 == nil {
return root1
}
node := &TreeNode{Val: root1.Val + root2.Val}
node.Left = mergeTrees(root1.Left, root2.Left)
node.Right = mergeTrees(root1.Right, root2.Right)
return node
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function mergeTrees(
root1: TreeNode | null,
root2: TreeNode | null,
): TreeNode | null {
if (root1 == null && root2 == null) return null;
if (root1 == null) return root2;
if (root2 == null) return root1;
let left = mergeTrees(root1.left, root2.left);
let right = mergeTrees(root1.right, root2.right);
return new TreeNode(root1.val + root2.val, left, right);
}// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
// #[inline]
// pub fn new(val: i32) -> Self {
// TreeNode {
// val,
// left: None,
// right: None
// }
// }
// }
use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
pub fn merge_trees(
root1: Option<Rc<RefCell<TreeNode>>>,
root2: Option<Rc<RefCell<TreeNode>>>,
) -> Option<Rc<RefCell<TreeNode>>> {
match (root1.is_some(), root2.is_some()) {
(false, false) => None,
(true, false) => root1,
(false, true) => root2,
(true, true) => {
{
let mut r1 = root1.as_ref().unwrap().borrow_mut();
let mut r2 = root2.as_ref().unwrap().borrow_mut();
r1.val += r2.val;
r1.left = Self::merge_trees(r1.left.take(), r2.left.take());
r1.right = Self::merge_trees(r1.right.take(), r2.right.take());
}
root1
}
}
}
}/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root1
* @param {TreeNode} root2
* @return {TreeNode}
*/
var mergeTrees = function (root1, root2) {
if (!root1) {
return root2;
}
if (!root2) {
return root1;
}
const node = new TreeNode(root1.val + root2.val);
node.left = mergeTrees(root1.left, root2.left);
node.right = mergeTrees(root1.right, root2.right);
return node;
};