README.md

498. 对角线遍历

English Version

题目描述

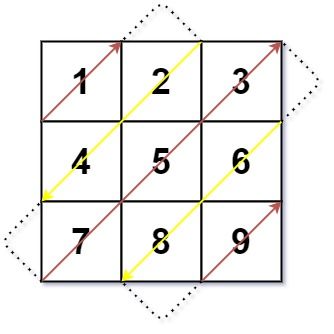
给你一个大小为 m x n 的矩阵 mat ，请以对角线遍历的顺序，用一个数组返回这个矩阵中的所有元素。

 

示例 1：

输入：mat = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,4,7,5,3,6,8,9]

示例 2：

输入：mat = [[1,2],[3,4]]
输出：[1,2,3,4]

 

提示：

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 104
• 1 <= m * n <= 104
• -105 <= mat[i][j] <= 105

解法

方法一：定点遍历

对于每一轮 $k$，我们固定从右上方开始往左下方遍历，得到 $t$。如果 $k$ 为偶数，再将 $t$ 逆序。然后将 $t$ 添加到结果数组 ans 中。

问题的关键在于确定轮数以及每一轮的起始坐标点 $(i,j)$。

时间复杂度 $O(m\times n)$。其中 $m$ 和 $n$ 分别为矩阵的行数和列数。

Python3

class Solution:
    def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:
        m, n = len(mat), len(mat[0])
        ans = []
        for k in range(m + n - 1):
            t = []
            i = 0 if k < n else k - n + 1
            j = k if k < n else n - 1
            while i < m and j >= 0:
                t.append(mat[i][j])
                i += 1
                j -= 1
            if k % 2 == 0:
                t = t[::-1]
            ans.extend(t)
        return ans

Java

class Solution {
    public int[] findDiagonalOrder(int[][] mat) {
        int m = mat.length, n = mat[0].length;
        int[] ans = new int[m * n];
        int idx = 0;
        List<Integer> t = new ArrayList<>();
        for (int k = 0; k < m + n - 1; ++k) {
            int i = k < n ? 0 : k - n + 1;
            int j = k < n ? k : n - 1;
            while (i < m && j >= 0) {
                t.add(mat[i][j]);
                ++i;
                --j;
            }
            if (k % 2 == 0) {
                Collections.reverse(t);
            }
            for (int v : t) {
                ans[idx++] = v;
            }
            t.clear();
        }
        return ans;
    }
}

C++

class Solution {
public:
    vector<int> findDiagonalOrder(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();
        vector<int> ans;
        vector<int> t;
        for (int k = 0; k < m + n - 1; ++k) {
            int i = k < n ? 0 : k - n + 1;
            int j = k < n ? k : n - 1;
            while (i < m && j >= 0) t.push_back(mat[i++][j--]);
            if (k % 2 == 0) reverse(t.begin(), t.end());
            for (int& v : t) ans.push_back(v);
            t.clear();
        }
        return ans;
    }
};

Go

func findDiagonalOrder(mat [][]int) []int {
	m, n := len(mat), len(mat[0])
	var ans []int
	for k := 0; k < m+n-1; k++ {
		var t []int
		i, j := k-n+1, n-1
		if k < n {
			i, j = 0, k
		}
		for i < m && j >= 0 {
			t = append(t, mat[i][j])
			i++
			j--
		}
		if k%2 == 0 {
			p, q := 0, len(t)-1
			for p < q {
				t[p], t[q] = t[q], t[p]
				p++
				q--
			}
		}
		for _, v := range t {
			ans = append(ans, v)
		}
	}
	return ans
}

TypeScript

function findDiagonalOrder(mat: number[][]): number[] {
    const res = [];
    const m = mat.length;
    const n = mat[0].length;
    let i = 0;
    let j = 0;
    let mark = true;
    while (res.length !== n * m) {
        if (mark) {
            while (i >= 0 && j < n) {
                res.push(mat[i][j]);
                i--;
                j++;
            }
            if (j === n) {
                j--;
                i++;
            }
            i++;
        } else {
            while (i < m && j >= 0) {
                res.push(mat[i][j]);
                i++;
                j--;
            }
            if (i === m) {
                i--;
                j++;
            }
            j++;
        }
        mark = !mark;
    }
    return res;
}

Rust

impl Solution {
    pub fn find_diagonal_order(mat: Vec<Vec<i32>>) -> Vec<i32> {
        let (m, n) = (mat.len(), mat[0].len());
        let (mut i, mut j) = (0, 0);
        (0..m * n)
            .map(|_| {
                let res = mat[i][j];
                if (i + j) % 2 == 0 {
                    if j == n - 1 {
                        i += 1;
                    } else if i == 0 {
                        j += 1;
                    } else {
                        i -= 1;
                        j += 1;
                    }
                } else {
                    if i == m - 1 {
                        j += 1;
                    } else if j == 0 {
                        i += 1;
                    } else {
                        i += 1;
                        j -= 1;
                    }
                }
                res
            })
            .collect()
    }
}

...