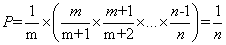给你一个可能含有 重复元素 的整数数组 nums ,请你随机输出给定的目标数字 target 的索引。你可以假设给定的数字一定存在于数组中。
实现 Solution 类:
Solution(int[] nums)用数组nums初始化对象。int pick(int target)从nums中选出一个满足nums[i] == target的随机索引i。如果存在多个有效的索引,则每个索引的返回概率应当相等。
示例:
输入 ["Solution", "pick", "pick", "pick"] [[[1, 2, 3, 3, 3]], [3], [1], [3]] 输出 [null, 4, 0, 2] 解释 Solution solution = new Solution([1, 2, 3, 3, 3]); solution.pick(3); // 随机返回索引 2, 3 或者 4 之一。每个索引的返回概率应该相等。 solution.pick(1); // 返回 0 。因为只有 nums[0] 等于 1 。 solution.pick(3); // 随机返回索引 2, 3 或者 4 之一。每个索引的返回概率应该相等。
提示:
1 <= nums.length <= 2 * 104-231 <= nums[i] <= 231 - 1target是nums中的一个整数- 最多调用
pick函数104次
蓄水池抽样问题。即从一个包含 n 个对象的列表 S 中随机选取 k 个对象,n 为一个非常大或者不知道的值。通常情况下,n 是一个非常大的值,大到无法一次性把所有列表 S 中的对象都放到内存中。我们这个问题是蓄水池抽样问题的一个特例,即 k=1。
解法:我们总是选择第一个对象,以 1/2 的概率选择第二个,以 1/3 的概率选择第三个,以此类推,以 1/m 的概率选择第 m 个对象。当该过程结束时,每一个对象具有相同的选中概率,即 1/n。
证明:第 m 个对象最终被选中的概率 P = 选择 m 的概率 × 其后面所有对象不被选择的概率,即:
思路同:382. 链表随机节点
class Solution:
def __init__(self, nums: List[int]):
self.nums = nums
def pick(self, target: int) -> int:
n = ans = 0
for i, v in enumerate(self.nums):
if v == target:
n += 1
x = random.randint(1, n)
if x == n:
ans = i
return ans
# Your Solution object will be instantiated and called as such:
# obj = Solution(nums)
# param_1 = obj.pick(target)class Solution {
private int[] nums;
private Random random = new Random();
public Solution(int[] nums) {
this.nums = nums;
}
public int pick(int target) {
int n = 0, ans = 0;
for (int i = 0; i < nums.length; ++i) {
if (nums[i] == target) {
++n;
int x = 1 + random.nextInt(n);
if (x == n) {
ans = i;
}
}
}
return ans;
}
}
/**
* Your Solution object will be instantiated and called as such:
* Solution obj = new Solution(nums);
* int param_1 = obj.pick(target);
*/class Solution {
public:
vector<int> nums;
Solution(vector<int>& nums) {
this->nums = nums;
}
int pick(int target) {
int n = 0, ans = 0;
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] == target) {
++n;
int x = 1 + rand() % n;
if (n == x) ans = i;
}
}
return ans;
}
};
/**
* Your Solution object will be instantiated and called as such:
* Solution* obj = new Solution(nums);
* int param_1 = obj->pick(target);
*/type Solution struct {
nums []int
}
func Constructor(nums []int) Solution {
return Solution{nums}
}
func (this *Solution) Pick(target int) int {
n, ans := 0, 0
for i, v := range this.nums {
if v == target {
n++
x := 1 + rand.Intn(n)
if n == x {
ans = i
}
}
}
return ans
}
/**
* Your Solution object will be instantiated and called as such:
* obj := Constructor(nums);
* param_1 := obj.Pick(target);
*/