README.md

113. 路径总和 II

English Version

题目描述

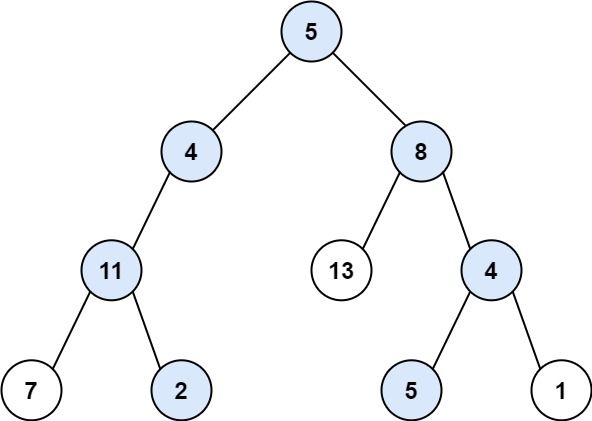
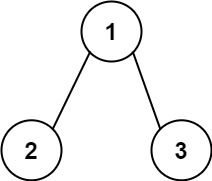
给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

 

示例 1：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：

输入：root = [1,2], targetSum = 0
输出：[]

 

提示：

• 树中节点总数在范围 [0, 5000] 内
• -1000 <= Node.val <= 1000
• -1000 <= targetSum <= 1000

解法

方法一：DFS

我们从根节点开始，递归遍历所有从根节点到叶子节点的路径，并记录路径和。当遍历到叶子节点时，如果此时路径和等于 targetSum，则将此路径加入答案。

时间复杂度 $O(n^2)$，其中 $n$ 是二叉树的节点数。空间复杂度 $O(n)$。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
        def dfs(root, s):
            if root is None:
                return
            s += root.val
            t.append(root.val)
            if root.left is None and root.right is None and s == targetSum:
                ans.append(t[:])
            dfs(root.left, s)
            dfs(root.right, s)
            t.pop()

        ans = []
        t = []
        dfs(root, 0)
        return ans

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private List<List<Integer>> ans = new ArrayList<>();
    private List<Integer> t = new ArrayList<>();

    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        dfs(root, targetSum);
        return ans;
    }

    private void dfs(TreeNode root, int s) {
        if (root == null) {
            return;
        }
        s -= root.val;
        t.add(root.val);
        if (root.left == null && root.right == null && s == 0) {
            ans.add(new ArrayList<>(t));
        }
        dfs(root.left, s);
        dfs(root.right, s);
        t.remove(t.size() - 1);
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        vector<vector<int>> ans;
        vector<int> t;
        function<void(TreeNode*, int)> dfs = [&](TreeNode* root, int s) {
            if (!root) return;
            s -= root->val;
            t.emplace_back(root->val);
            if (!root->left && !root->right && s == 0) ans.emplace_back(t);
            dfs(root->left, s);
            dfs(root->right, s);
            t.pop_back();
        };
        dfs(root, targetSum);
        return ans;
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func pathSum(root *TreeNode, targetSum int) (ans [][]int) {
	t := []int{}
	var dfs func(*TreeNode, int)
	dfs = func(root *TreeNode, s int) {
		if root == nil {
			return
		}
		s -= root.Val
		t = append(t, root.Val)
		if root.Left == nil && root.Right == nil && s == 0 {
			cp := make([]int, len(t))
			copy(cp, t)
			ans = append(ans, cp)
		}
		dfs(root.Left, s)
		dfs(root.Right, s)
		t = t[:len(t)-1]
	}
	dfs(root, targetSum)
	return
}

Rust

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    fn dfs(
        root: Option<Rc<RefCell<TreeNode>>>,
        paths: &mut  Vec<i32>,
        mut target_sum: i32,
        res: &mut Vec<Vec<i32>>,
    ) {
        if let Some(node) = root {
            let mut node = node.borrow_mut();
            target_sum -= node.val;
            paths.push(node.val);
            if node.left.is_none() && node.right.is_none() {
                if target_sum == 0 {
                    res.push(paths.clone());
                }
            } else {
                if node.left.is_some() {
                    Self::dfs(node.left.take(), paths, target_sum, res);
                }
                if node.right.is_some() {
                    Self::dfs(node.right.take(), paths, target_sum, res);
                }
            }
            paths.pop();
        }
    }

    pub fn path_sum(root: Option<Rc<RefCell<TreeNode>>>, target_sum: i32) -> Vec<Vec<i32>> {
        let mut res = vec![];
        let mut paths = vec![];
        Self::dfs(root, &mut paths,  target_sum, &mut res);
        res
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {number[][]}
 */
var pathSum = function (root, targetSum) {
    const ans = [];
    const t = [];
    function dfs(root, s) {
        if (!root) return;
        s -= root.val;
        t.push(root.val);
        if (!root.left && !root.right && s == 0) ans.push([...t]);
        dfs(root.left, s);
        dfs(root.right, s);
        t.pop();
    }
    dfs(root, targetSum);
    return ans;
};

...