Skip to content

Latest commit

 

History

History
309 lines (251 loc) · 7.91 KB

README.md

File metadata and controls

309 lines (251 loc) · 7.91 KB
Raw

97. 交错字符串

English Version

题目描述

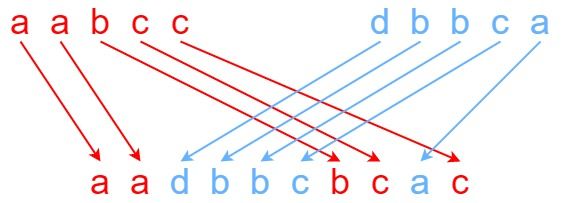
给定三个字符串 s1、s2、s3，请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。

两个字符串 s 和 t 交错 的定义与过程如下，其中每个字符串都会被分割成若干 非空 子字符串：

  • s = s1 + s2 + ... + sn
  • t = t1 + t2 + ... + tm
  • |n - m| <= 1
  • 交错 是 s1 + t1 + s2 + t2 + s3 + t3 + ... 或者 t1 + s1 + t2 + s2 + t3 + s3 + ...

注意：a + b 意味着字符串 a 和 b 连接。

 

示例 1：

输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
输出：true

示例 2：

输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
输出：false

示例 3：

输入：s1 = "", s2 = "", s3 = ""
输出：true

 

提示：

  • 0 <= s1.length, s2.length <= 100
  • 0 <= s3.length <= 200
  • s1、s2、和 s3 都由小写英文字母组成

 

进阶：您能否仅使用 O(s2.length) 额外的内存空间来解决它?

解法

题目描述带有一定迷惑性，“交错”的过程其实就类似归并排序的 merge 过程，每次从 s1 或 s2 的首部取一个字符，最终组成 s3，用记忆化搜索或者动态规划都可以解决。

Python3

class Solution:
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        m, n = len(s1), len(s2)
        if m + n != len(s3):
            return False

        @cache
        def dfs(i, j):
            if i == m and j == n:
                return True

            return (
                i < m
                and s1[i] == s3[i + j]
                and dfs(i + 1, j)
                or j < n
                and s2[j] == s3[i + j]
                and dfs(i, j + 1)
            )

        return dfs(0, 0)
class Solution:
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        m, n = len(s1), len(s2)
        if m + n != len(s3):
            return False
        dp = [[False] * (n + 1) for _ in range(m + 1)]
        dp[0][0] = True
        for i in range(m + 1):
            for j in range(n + 1):
                k = i + j - 1
                if i:
                    dp[i][j] = s1[i - 1] == s3[k] and dp[i - 1][j]
                if j:
                    dp[i][j] |= (s2[j - 1] == s3[k] and dp[i][j - 1])
        return dp[-1][-1]
class Solution:
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        m, n = len(s1), len(s2)
        if m + n != len(s3):
            return False
        dp = [False] * (n + 1)
        dp[0] = True
        for i in range(m + 1):
            for j in range(n + 1):
                k = i + j - 1
                if i:
                    dp[j] &= (s1[i - 1] == s3[k])
                if j:
                    dp[j] |= (s2[j - 1] == s3[k] and dp[j - 1])
        return dp[-1]

Java

class Solution {
    private int m;
    private int n;
    private String s1;
    private String s2;
    private String s3;
    private Map<Integer, Boolean> memo = new HashMap<>();

    public boolean isInterleave(String s1, String s2, String s3) {
        m = s1.length();
        n = s2.length();
        this.s1 = s1;
        this.s2 = s2;
        this.s3 = s3;
        if (m + n != s3.length()) {
            return false;
        }
        return dfs(0, 0);
    }

    private boolean dfs(int i, int j) {
        System.out.println(i + ", " + j);
        if (i == m && j == n) {
            return true;
        }
        if (memo.containsKey(i * 100 + j)) {
            return memo.get(i * 100 + j);
        }

        boolean ret = (i < m && s1.charAt(i) == s3.charAt(i + j) && dfs(i + 1, j)) ||
                (j < n && s2.charAt(j) == s3.charAt(i + j) && dfs(i, j + 1));

        memo.put(i * 100 + j, ret);
        return ret;
    }
}
class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        int m = s1.length(), n = s2.length();
        if (m + n != s3.length()) {
            return false;
        }
        boolean[] dp = new boolean[n + 1];
        dp[0] = true;
        for (int i = 0; i <= m; ++i) {
            for (int j = 0; j <= n; ++j) {
                int k = i + j - 1;
                if (i > 0) {
                    dp[j] &= (s1.charAt(i - 1) == s3.charAt(k));
                }
                if (j > 0) {
                    dp[j] |= (s2.charAt(j - 1) == s3.charAt(k) && dp[j - 1]);
                }
            }
        }
        return dp[n];
    }
}

C++

class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        int m = s1.size(), n = s2.size();
        if (m + n != s3.size()) return false;

        unordered_map<int, bool> memo;

        function<bool(int, int)> dfs;
        dfs = [&](int i, int j) {
            if (i == m && j == n) return true;
            auto it = memo.find(i * 100 + j);
            if (it != memo.end()) return it->second;

            bool ret = (i < m && s1[i] == s3[i + j] && dfs(i + 1, j)) || (j < n && s2[j] == s3[i + j] && dfs(i, j + 1));

            memo[i * 100 + j] = ret;
            return ret;
        };

        return dfs(0, 0);
    }
};
class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        int m = s1.size(), n = s2.size();
        if (m + n != s3.size()) return false;
        vector<int> dp(n + 1);
        dp[0] = 1;
        for (int i = 0; i <= m; ++i)
        {
            for (int j = 0; j <= n; ++j)
            {
                int k = i + j - 1;
                if (i) dp[j] &= (s1[i - 1] == s3[k]);
                if (j) dp[j] |= (s2[j - 1] == s3[k] && dp[j - 1]);
            }
        }
        return dp[n];
    }
};

Go

func isInterleave(s1 string, s2 string, s3 string) bool {
	m, n := len(s1), len(s2)
	if m+n != len(s3) {
		return false
	}

	memo := make(map[int]bool)

	var dfs func(int, int) bool
	dfs = func(i, j int) bool {
		if i == m && j == n {
			return true
		}
		if v, ok := memo[i*100+j]; ok {
			return v
		}

		ret := (i < m && s1[i] == s3[i+j] && dfs(i+1, j)) ||
			(j < n && s2[j] == s3[i+j] && dfs(i, j+1))

		memo[i*100+j] = ret
		return ret
	}

	return dfs(0, 0)
}
func isInterleave(s1 string, s2 string, s3 string) bool {
	m, n := len(s1), len(s2)
	if m+n != len(s3) {
		return false
	}
	dp := make([]bool, n+1)
	dp[0] = true
	for i := 0; i <= m; i++ {
		for j := 0; j <= n; j++ {
			k := i + j - 1
			if i > 0 {
				dp[j] = dp[j] && (s1[i-1] == s3[k])
			}
			if j > 0 {
				dp[j] = dp[j] || (s2[j-1] == s3[k] && dp[j-1])
			}
		}
	}
	return dp[n]
}

...