作者: 负雪明烛 id: fuxuemingzhu 个人博客: http://fuxuemingzhu.cn/
@TOC
题目地址:https://leetcode.com/problems/regions-cut-by-slashes/description/
In a N x N grid composed of 1 x 1 squares, each 1 x 1 square consists of a /, \, or blank space. These characters divide the square into contiguous regions.
(Note that backslash characters are escaped, so a \ is represented as "\\".)
Return the number of regions.
Example 1:
Input:
[
" /",
"/ "
]
Output: 2
Explanation: The 2x2 grid is as follows:
Example 2:
Input:
[
" /",
" "
]
Output: 1
Explanation: The 2x2 grid is as follows:
Example 3:
Input:
[
"\\/",
"/\\"
]
Output: 4
Explanation: (Recall that because \ characters are escaped, "\\/" refers to \/, and "/\\" refers to /\.)
The 2x2 grid is as follows:
Example 4:
Input:
[
"/\\",
"\\/"
]
Output: 5
Explanation: (Recall that because \ characters are escaped, "/\\" refers to /\, and "\\/" refers to \/.)
The 2x2 grid is as follows:
Example 5:
Input:
[
"//",
"/ "
]
Output: 3
Explanation: The 2x2 grid is as follows:
Note:
1 <= grid.length == grid[0].length <= 30grid[i][j]is either'/','\', or' '.
有个N*N的格子,每个格子有三种状态,左划线,右划线,没有线。给出了每个格子的状态之后,求最后这些线能把格子分割成多少个不同的区域。
下面举例说明题目的意思。
假如输入是 :
[
"/\\",
"\\/"
]
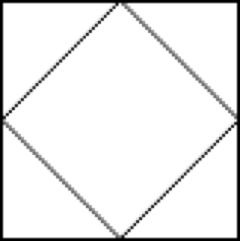
则其对应的形状是:
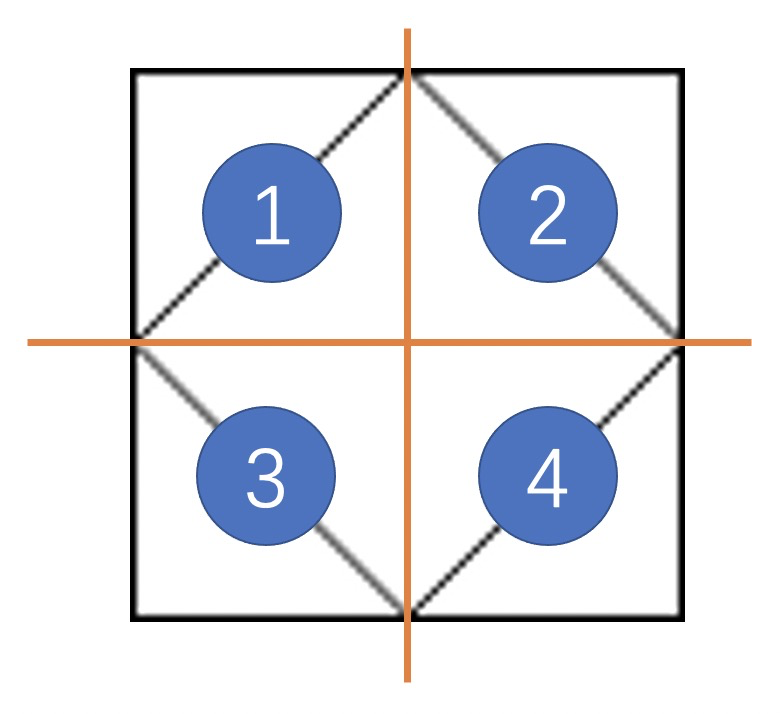
理解方式:首先根据输入我们知道这个格子是 2 * 2 的,对应了下图的 4 个格子。第一行第一个字符是 "/",它对应了下图中 ①,其含义是格子内有个左划线。第一行第二个字符是 "\",它是转义之后的 "",即在程序中它其实只是一个 "",只不过打印出来会成为 "\",它对应了下图中 ②,其含义是格子内有个右划线。第二行的两个字符对应了下图的③④。
我们得到了上图之后,题目要求的是上图中有多少个区域,答案是 5。即有中间 1 个正方形,正方形周围有 4 个三角形。
本题的题目意思相对较难理解,务必理解题目之后再继续阅读。
连通区域的问题,一般都可以使用 并查集 解决。并查集分为 “并” 与 “查” 两部分。“并” 的部分,表示让两个区域连通;“查” 的部分,表示检查两个区域是否连通。本文由于篇幅受限,不详细展开。
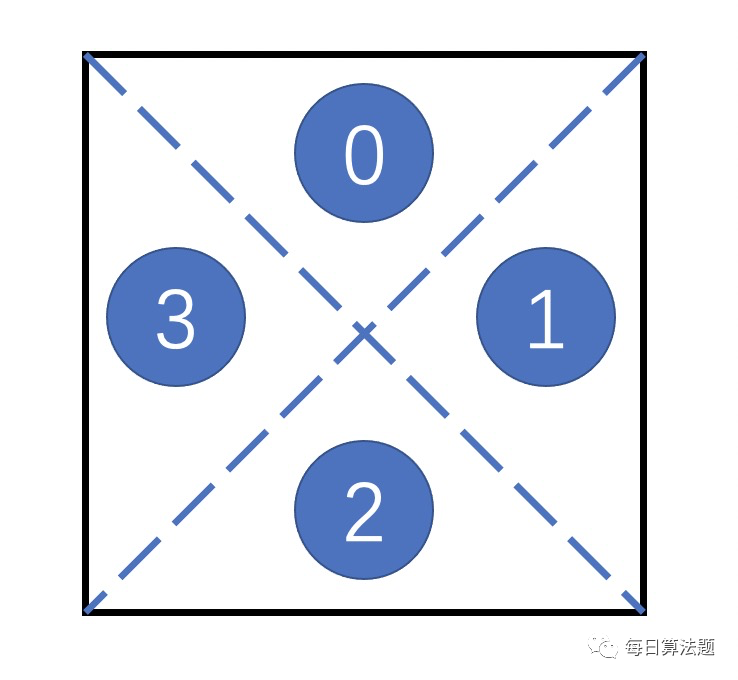
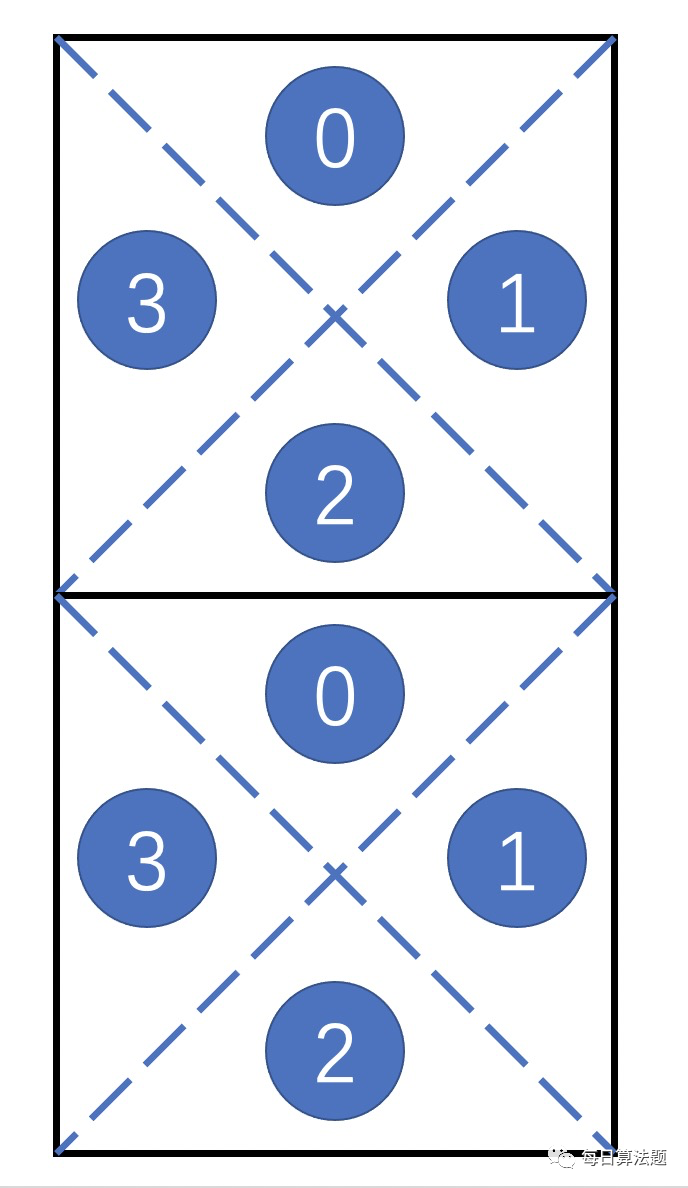
为了解决本题,我们把 一个格子 划分成 4 个区域。如果是 左划线 "/",即对应了下图的 0️⃣ 和 ③ 连通、① 和 ② 连通;如果是 右划线 "\",即对应了下图的 0️⃣ 和 ① 连通、③ 和 ② 连通;如果格子内没有线 " ",则 4 个区域都连通。
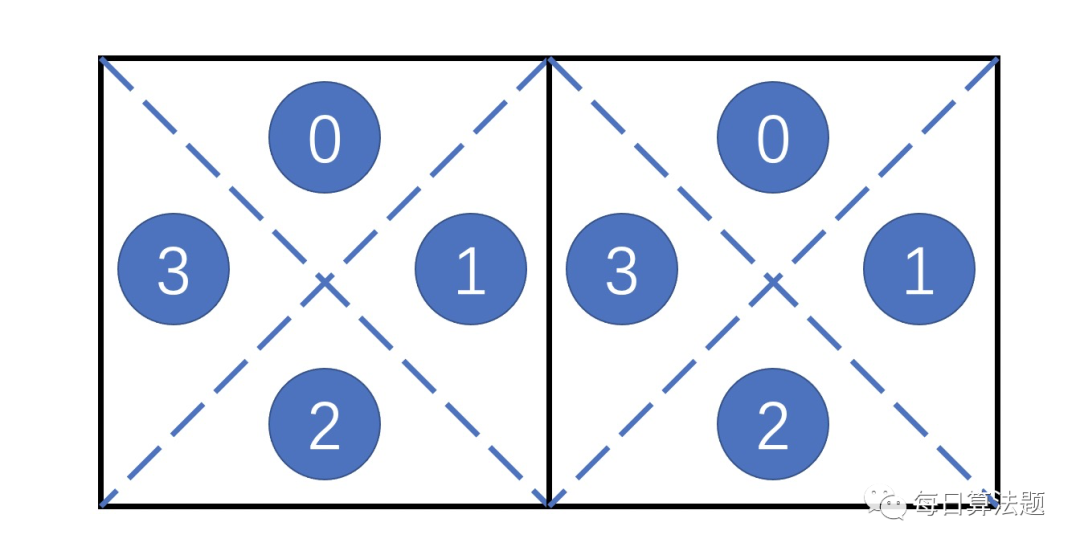
对于相邻的格子,有两种情况,一种是左右相邻,一种是上下相邻。
- 左右相邻的两个格子,是左边格子的 ① 和右边格子的 ③ 连通。
- 上下相邻的两个格子,是上边格子的 ② 和下边格子的 0️⃣ 相邻。
经过上面的这么多分析,我们终于有了解题思路:遍历每个格子,判断这个格子内的连通方式,并且判断这个格子和其上边、左边格子的连通方式。
我们使用了并查集的模板,包括 “并” 的函数 union(), “查” 的函数 find()。这两个函数是和题目无关的模板,可以在各个题目中直接使用。
又定义了一个函数 position(self, r, c, i),该函数的含义是获取第 r 行、第 c 列的格子的第 i 个位置的编号。r 和 c 是我们遍历题目中各个格子时的位置,而 i 则是我们上图给每个格子划分出的 4 个区域的编号。
题目给出的几个例子都是 2 * 2 的,但是实际上可以是 N * N 的,N 为数组的长度、宽度。m_ 表示并查集的大小,对应了所有格子的所有区域,即 N * N * 4。count 表示题目给的图有多少连通区域,初始时假设每个区域都不连通,在并查集的 union() 过程中,每次合并都会减少一个不连通区域,因此最终的 count 值就是本题要求的连通区域的结果。
下面的代码是 Python 实现的,两重 for 循环对每个格子进行遍历,w 变量是每个格子的字符,取值可能为 "/","\"," " 三种状态。
- 如果当前的行 row > 0,这个格子的 0️⃣ 需要跟它上面格子的 ② 连通;
- 如果当前的列 col > 0,这个格子的 ③ 需要跟它左边格子的 ① 连通。
- 如果当前格子的状态是 "/",则当前格子的 0️⃣ 和 ③ 连通、① 和 ② 连通;
- 如果当前格子的状态是 "\",即对应了下图的 0️⃣ 和 ① 连通、③ 和 ② 连通;
- 如果格子内没有线,则 4 个区域都连通。
下面的代码判断格子的内容时,使用了 "!=",其主要目的是为了节省当格子内没有线的时候代码,留给读者自行分析。
class Solution(object):
def regionsBySlashes(self, grid):
"""
:type grid: List[str]
:rtype: int
"""
self.N = len(grid)
m_ = range(self.N * self.N * 4)
self.count = self.N * self.N * 4
for row in range(self.N):
line = grid[row]
for col in range(self.N):
w = line[col]
if row > 0:
self.union(m_, self.position(row - 1, col, 2), self.position(row, col, 0))
if col > 0:
self.union(m_, self.position(row, col - 1, 1), self.position(row, col, 3))
if w != '/':
self.union(m_, self.position(row, col, 0), self.position(row, col, 1))
self.union(m_, self.position(row, col, 3), self.position(row, col, 2))
if w != '\\':
self.union(m_, self.position(row, col, 0), self.position(row, col, 3))
self.union(m_, self.position(row, col, 1), self.position(row, col, 2))
return self.count
def find(self, m_, a):
if m_[a] == a:
return a
return self.find(m_, m_[a])
def union(self, m_, a, b):
pa = self.find(m_, a)
pb = self.find(m_, b)
if (pa == pb):
return
m_[pa] = pb
self.count -= 1
def position(self, r, c, i):
return (r * self.N + c) * 4 + i算法每日一题是个互相帮助、互相监督的力扣打卡网站,其地址是 https://www.ojeveryday.com/
想加入千人刷题群的朋友,可以复制上面的链接到浏览器,然后在左侧点击“加入组织”,提交力扣个人主页,即可进入刷题群。期待你早日加入。
参考资料:https://www.youtube.com/watch?v=Mia50ouW1T4
2018 年 12 月 16 日 —— 周赛好难 2021 年 1 月 25 日 —— 重写刷了这个题,并推送了微信公众号