作者: 负雪明烛 id: fuxuemingzhu 个人博客: http://fuxuemingzhu.cn/
@TOC
题目地址:https://leetcode.com/problems/projection-area-of-3d-shapes/description/
On a N * N grid, we place some 1 * 1 * 1 cubes that are axis-aligned with the x, y, and z axes.
Each value v = grid[i][j] represents a tower of v cubes placed on top of grid cell (i, j).
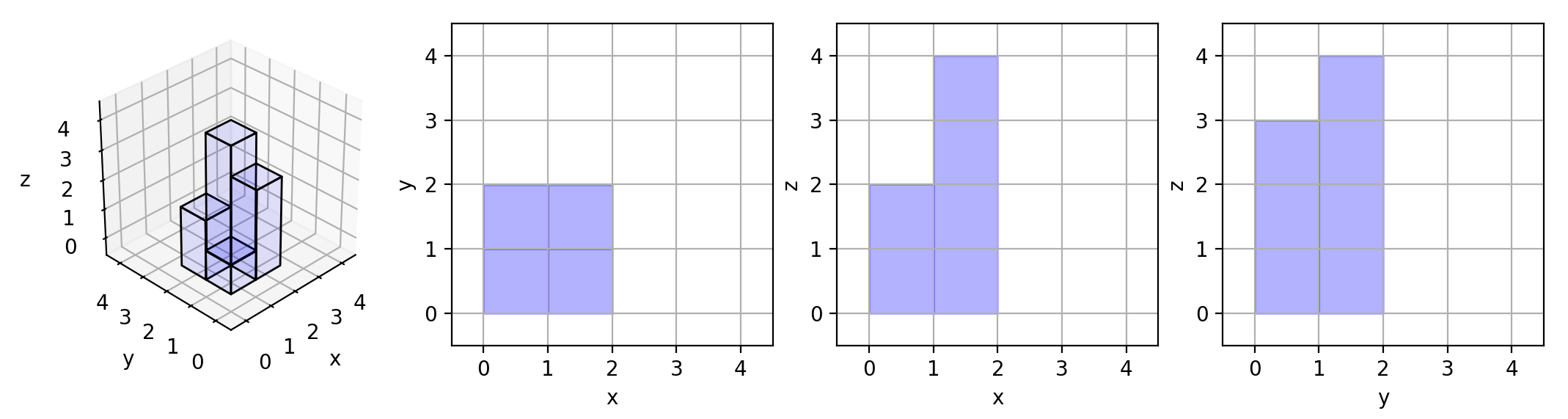
Now we view the projection of these cubes onto the xy, yz, and zx planes.
A projection is like a shadow, that maps our 3 dimensional figure to a 2 dimensional plane.
Here, we are viewing the "shadow" when looking at the cubes from the top, the front, and the side.
Return the total area of all three projections.
Example 1:
Input: [[2]]
Output: 5
Example 2:
Input: [[1,2],[3,4]]
Output: 17
Explanation:
Here are the three projections ("shadows") of the shape made with each axis-aligned plane.
Example 3:
Input: [[1,0],[0,2]]
Output: 8
Example 4:
Input: [[1,1,1],[1,0,1],[1,1,1]]
Output: 14
Example 5:
Input: [[2,2,2],[2,1,2],[2,2,2]]
Output: 21
Note:
- 1 <= grid.length = grid[0].length <= 50
- 0 <= grid[i][j] <= 50
给出了一个方阵,方阵里面的数值是柱子的高度,求三视图所有的阴影部分的面积。
稍微缕一下就能明白,俯视图投影就是不为0的柱子的个数,主视图、侧视图是当前视图柱子的最高值求和。
代码如下:
class Solution(object):
def projectionArea(self, grid):
"""
:type grid: List[List[int]]
:rtype: int
"""
top, front, side = 0, 0, 0
n = len(grid)
for i in range(n):
x, y = 0, 0
for j in range(n):
if grid[i][j] != 0:
top += 1
x = max(x, grid[i][j])
y = max(y, grid[j][i])
front += x
side += y
return top + front + side也可以三视图分别进行计算,似乎更清晰明了。
class Solution:
def projectionArea(self, grid):
"""
:type grid: List[List[int]]
:rtype: int
"""
M, N = len(grid), len(grid[0])
rowMax, colMax = [0] * M, [0] * N
xy = sum(0 if grid[i][j] == 0 else 1 for i in range(M) for j in range(N))
xz = sum(list(map(max, grid)))
yz = sum(list(map(max, [[grid[i][j] for i in range(M)] for j in range(N)])))
return xy + xz + yz2018 年 8 月 16 日 —— 一个月不写题,竟然啥都不会了。。加油! 2018 年 11 月 5 日 —— 打了羽毛球,有点累