- 作者: 负雪明烛
- id: fuxuemingzhu
- 公众号:负雪明烛
- 本文关键词:LeetCode,力扣,算法,算法题,滑动窗口,递归,前缀和,preSum,刷题群
@TOC
题目地址:https://leetcode-cn.com/problems/maximum-points-you-can-obtain-from-cards/
几张卡牌 排成一行,每张卡牌都有一个对应的点数。点数由整数数组 cardPoints 给出。
每次行动,你可以从行的开头或者末尾拿一张卡牌,最终你必须正好拿 k 张卡牌。
你的点数就是你拿到手中的所有卡牌的点数之和。
给你一个整数数组 cardPoints 和整数 k,请你返回可以获得的最大点数。
示例 1:
输入:cardPoints = [1,2,3,4,5,6,1], k = 3
输出:12
解释:第一次行动,不管拿哪张牌,你的点数总是 1 。但是,先拿最右边的卡牌将会最大化你的可获得点数。最优策略是拿右边的三张牌,最终点数为 1 + 6 + 5 = 12 。
示例 2:
输入:cardPoints = [2,2,2], k = 2
输出:4
解释:无论你拿起哪两张卡牌,可获得的点数总是 4 。
示例 3:
输入:cardPoints = [9,7,7,9,7,7,9], k = 7
输出:55
解释:你必须拿起所有卡牌,可以获得的点数为所有卡牌的点数之和。
示例 4:
输入:cardPoints = [1,1000,1], k = 1
输出:1
解释:你无法拿到中间那张卡牌,所以可以获得的最大点数为 1 。
示例 5:
输入:cardPoints = [1,79,80,1,1,1,200,1], k = 3
输出:202
提示:
1 <= cardPoints.length <= 10^51 <= cardPoints[i] <= 10^41 <= k <= cardPoints.length
你是不是跟我一样,拿到今天题目的第一想法是模拟题目取卡牌的过程呢?模拟的方法可以用递归。但是递归的过程是把所有的可能组合方式都求了一遍,时间复杂度会达到 O(N*k) ,在题目所给出的 10 ^ 5 的数据规模下,会超时。
下面的代码是我用的递归+记忆化的方式写的,虽然有记忆化,但是因为没有降低时间复杂度,所以仍然超时。提供在这里仅供大家参考。欢迎大家提供能 AC 的递归方法。
我定义的递归函数 dfs(cardPoints, i, j, k) ,表示在 cardPoints 的第 i ~ j 的位置中(包含i,j),从两端抽取 k 个卡牌能够获得的最大点数。那么当 k == 0 的时候,说明不抽牌,结果是 0。当 k != 0 的时候,抽取 k 个卡牌能拿到的点数等于 max(抽取最左边卡牌的点数 + 剩余卡牌继续抽获得的最大点数, 抽取最右边卡牌的点数 + 剩余卡牌继续抽获得最大点数)。
时间复杂度是 O(N ^ 2) 。
class Solution(object):
def maxScore(self, cardPoints, k):
"""
:type cardPoints: List[int]
:type k: int
:rtype: int
"""
N = len(cardPoints)
self.memo = {}
return self.dfs(cardPoints, 0, N - 1, k)
def dfs(self, cardPoints, i, j, k):
if k == 0:
return 0
if (i, j) in self.memo:
return self.memo[(i, j)]
removeLeft = cardPoints[i] + self.dfs(cardPoints, i + 1, j, k - 1)
removeRight = cardPoints[j] + self.dfs(cardPoints, i, j - 1, k - 1)
res = max(removeLeft, removeRight)
self.memo[(i, j)] = res
return res当数据规模到达了 10 ^ 5 ,已经在提醒我们这个题应该使用 O(N) 的解法。
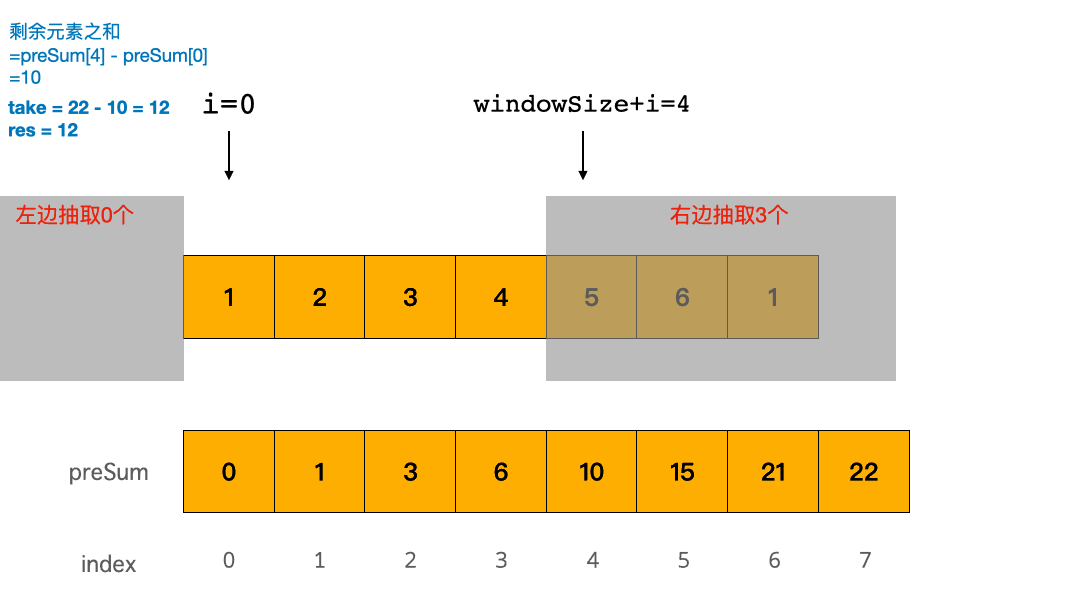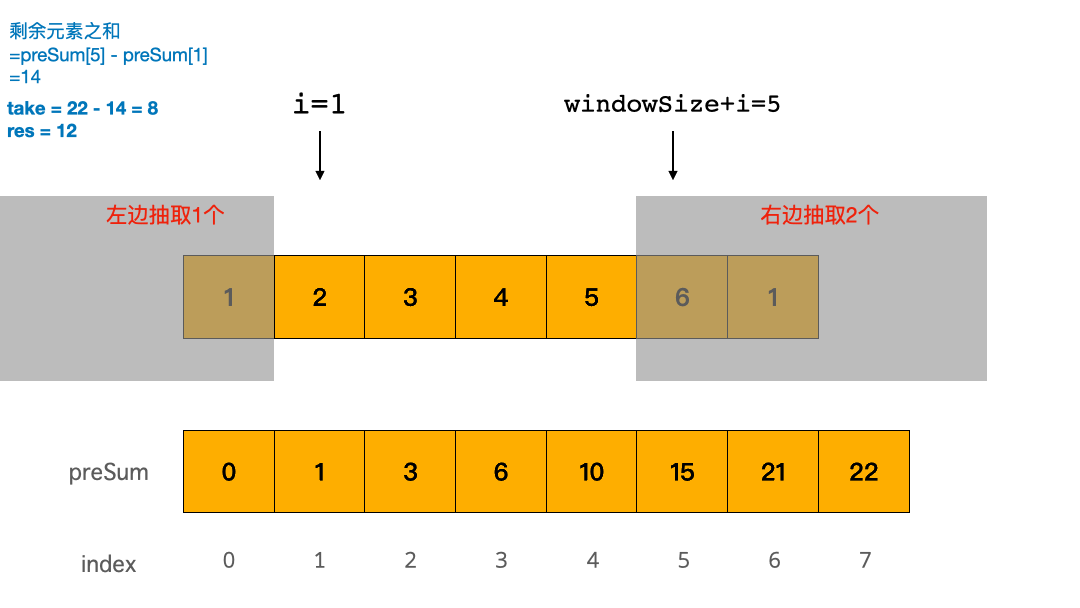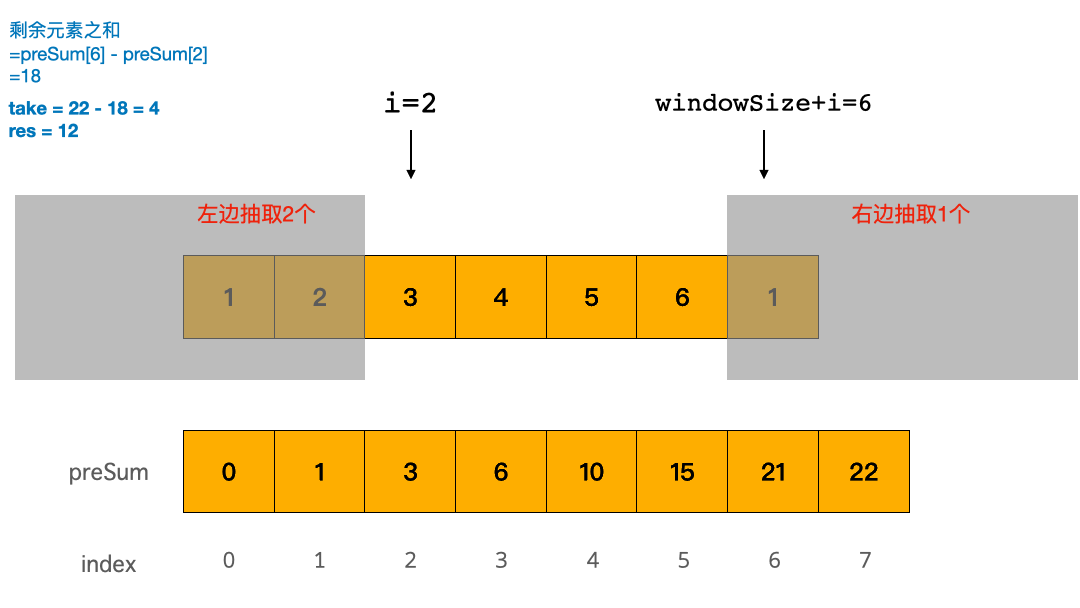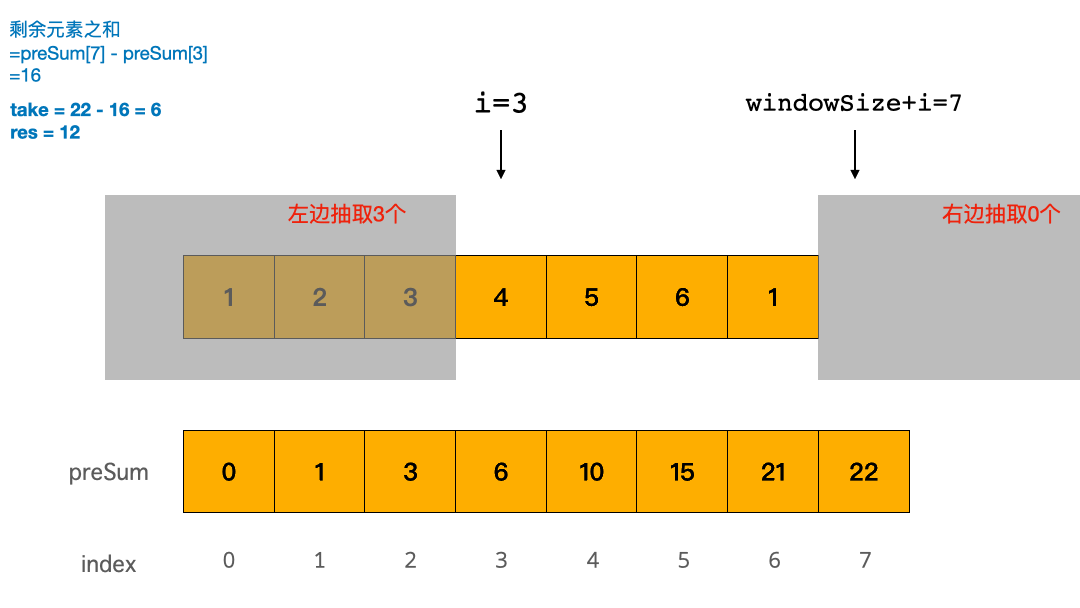
把今天的这个问题思路整理一下,题目等价于:求从 cardPoints 最左边抽 i 个数字,从 cardPoints 最右边抽取 k - i 个数字,能抽取获得的最大点数是多少。
一旦这么想,立马柳暗花明:抽走的卡牌点数之和 = cardPoints 所有元素之和 - 剩余的中间部分元素之和。
我们同样使用模拟法,但是比递归方法高妙的地方在,我们一次性从左边抽走 i 个数字: i 从 0 到 k 的遍历,表示从左边抽取了的元素数,那么从右边抽取的元素数是 k - i 个。现在问题是怎么快速求 剩余的中间部分元素之和?
没错,preSum!我的题解中已经多次分享过 preSum 的思想,下面是 preSum 的介绍,已经看过我前几天题解的朋友可以直接跳过。
求区间的和可以用 preSum 。 preSum 方法还能快速计算指定区间段 i ~ j 的元素之和。它的计算方法是从左向右遍历数组,当遍历到数组的 i 位置时, preSum 表示 i 位置左边的元素之和。
假设数组长度为 N ,我们定义一个长度为 N+1 的 preSum 数组, preSum[i] 表示该元素左边所有元素之和(不包含当前元素)。然后遍历一次数组,累加区间 [0, i) 范围内的元素,可以得到 preSum 数组。代码如下:
N = len(nums)
preSum = range(N + 1)
for i in range(N):
preSum[i + 1] = preSum[i] + nums[i]
print(preSum)利用 preSum 数组,可以在 O(1) 的时间内快速求出 nums 任意区间 [i, j] (两端都包含) 的各元素之和。
sum(i, j) = preSum[i + 1] - preSum[j]
综合以上的思路,我们的想法可以先求 preSum ,然后使用一个 0 ~ k 的遍历表示从左边拿走的元素数,然后根据窗口大小 windowSize = N - k ,利用 preSum 快速求窗口内元素之和。
对应的 Python 代码如下。
class Solution(object):
def maxScore(self, cardPoints, k):
"""
:type cardPoints: List[int]
:type k: int
:rtype: int
"""
N = len(cardPoints)
preSum = [0] * (N + 1)
for i in range(N):
preSum[i + 1] = preSum[i] + cardPoints[i]
res = float("inf")
windowSize = N - k
for i in range(k + 1):
res = min(res, preSum[windowSize + i] - preSum[i])
return preSum[N] - res在上面的 preSum 中,我们已经想到了,抽走的卡牌点数之和 = cardPoints 所有元素之和 - 剩余的中间部分元素之和。在 preSum 的代码里,我们是模拟了从左边拿走 i 个卡牌的过程。事实上,我们也可以直接求剩余的中间部分元素之和的最小值。只要剩余的卡牌点数之和最小,那么抽走的卡牌点数之和就最大!
求一个固定大小的窗口中所有元素之和的最小值——这是一个滑动窗口问题!与这个问题非常类似的就是前几天的每日一题 643. 子数组最大平均数 I。巧了,当时我的题解也是 preSum 和 滑动窗口 两种做法!
把剩余的中间部分元素抽象成长度固定为 windowSize = N - k 的滑动窗口。当每次窗口右移的时候,需要把右边的新位置 加到 窗口中的 和 中,把左边被移除的位置从窗口的 和 中 减掉。这样窗口里面所有元素的 和 是准确的,我们求出最大的和,最终除以 k 得到最大平均数。
这个方法只用遍历一次数组。
需要注意的是,需要根据 i 的位置,计算滑动窗口是否开始、是否要移除最左边元素:
- 当
i >= windowSize时,为了固定窗口的元素是k个,每次移动时需要将i - windowSize位置的元素移除。 - 当
i >= windowSize - 1时,滑动窗口内的元素刚好是k个,开始计算滑动窗口的最小和。
最后,用 cardPoints 的所有元素之和,减去滑动窗口内的最小元素和,就是拿走的卡牌的最大点数。
使用 Python2 写的代码如下。
class Solution(object):
def maxScore(self, cardPoints, k):
"""
:type cardPoints: List[int]
:type k: int
:rtype: int
"""
N = len(cardPoints)
windowSize = N - k # 窗口的大小
sums = 0
res = float("inf") # 正无穷大
for i in range(N):
sums += cardPoints[i]
if i >= windowSize:
sums -= cardPoints[i - windowSize]
if i >= windowSize - 1:
res = min(res, sums)
return sum(cardPoints) - res- 今天这个题目,难点还是需要把抽取卡牌的问题转变为一个滑动窗口的问题。
- 问题抽象之后,preSum 和 滑动窗口 两种解法就已经呼之欲出了。
- 每日一题的作用再次凸显,同一类题目都是换汤不换药,学会思路和套路之后,就很快秒杀!
算法每日一题是个互相帮助、互相监督的力扣打卡网站,其地址是 https://www.ojeveryday.com/
想加入千人刷题群的朋友,可以复制上面的链接到浏览器,然后在左侧点击“加入组织”,提交力扣个人主页,即可进入刷题群。期待你早日加入。
欢迎关注我的公众号:每日算法题
2021 年 2 月 6 日 —— 今天是年前的最后一个假期,没剪上头发