作者: 负雪明烛 id: fuxuemingzhu 个人博客: http://fuxuemingzhu.cn/
@TOC
题目地址:https://leetcode-cn.com/problems/car-pooling/
假设你是一位顺风车司机,车上最初有 capacity 个空座位可以用来载客。由于道路的限制,车 只能 向一个方向行驶(也就是说,不允许掉头或改变方向,你可以将其想象为一个向量)。
这儿有一份乘客行程计划表 trips[][],其中 trips[i] = [num_passengers, start_location, end_location] 包含了第 i 组乘客的行程信息:
- 必须接送的乘客数量;
- 乘客的上车地点;
- 以及乘客的下车地点。
这些给出的地点位置是从你的 初始 出发位置向前行驶到这些地点所需的距离(它们一定在你的行驶方向上)。
请你根据给出的行程计划表和车子的座位数,来判断你的车是否可以顺利完成接送所有乘客的任务(当且仅当你可以在所有给定的行程中接送所有乘客时,返回 true,否则请返回 false)。
示例 1:
输入:trips = [[2,1,5],[3,3,7]], capacity = 4
输出:false
示例 2:
输入:trips = [[2,1,5],[3,3,7]], capacity = 5
输出:true
示例 3:
输入:trips = [[2,1,5],[3,5,7]], capacity = 3
输出:true
示例 4:
输入:trips = [[3,2,7],[3,7,9],[8,3,9]], capacity = 11
输出:true
提示:
- 你可以假设乘客会自觉遵守 “先下后上” 的良好素质
trips.length <= 1000trips[i].length == 31 <= trips[i][0] <= 1000 <= trips[i][1] < trips[i][2] <= 10001 <= capacity <= 100000
有一辆车,在一个单向的路上行驶。给定了很多区间,每个区间都表示了这段区间上来的人数、上来的地点、下车的地点。已知车的容积,判断能否在路径中能装下所有的人。
本身这个题让我们判断路径中的最大人数是否超过车的装载能力。那么直觉的思路是:把每个区间的人数变化,求解到坐标系每个点上,最后求所有点中最大的人数。
但是这样的话,时间复杂度是 区间个数*区间大小。 当区间个数比较多、区间比较大的时候,会超时。
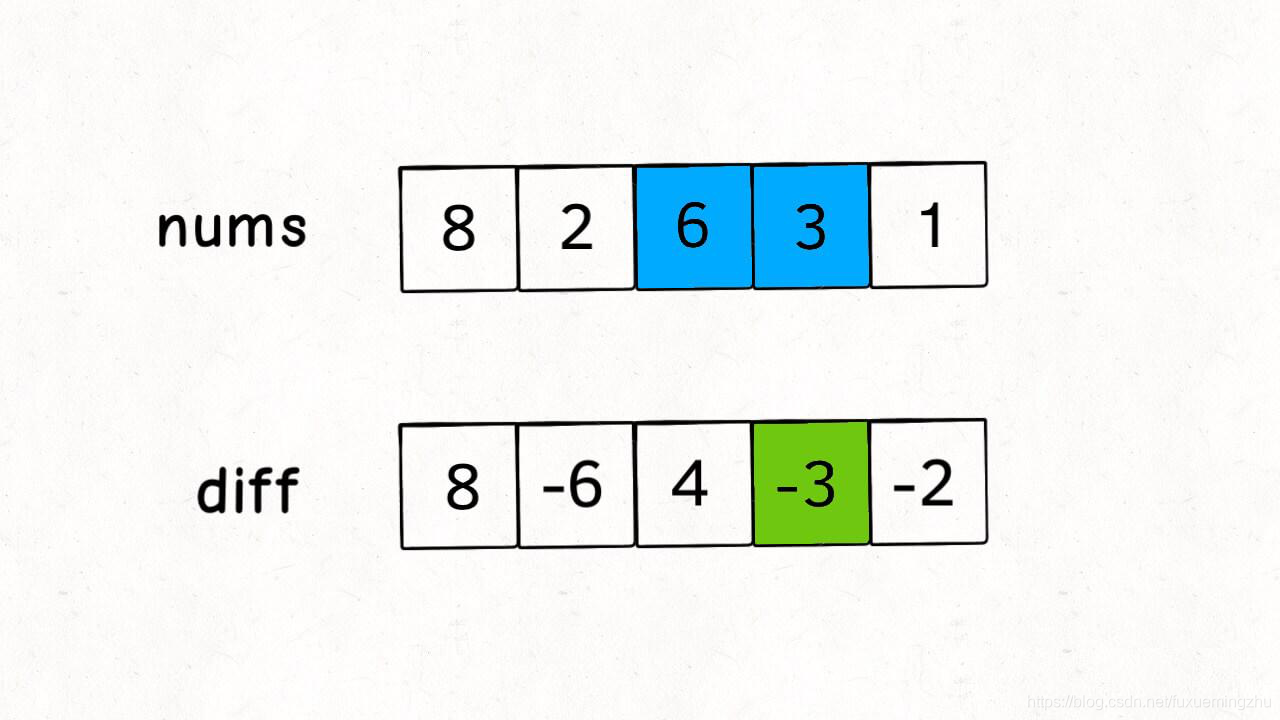
本题利用了一个很巧妙的方法:差分数组。
何为差分数组?不要被这个名字给吓到了,其实道理很简单。知道前缀和么?前缀和
这有啥用呢?当我们知道了数组的起始值,然后知道了每个位置和前面位置的差,那么通过累加差分数组,就可以恢复出原始的数组值。
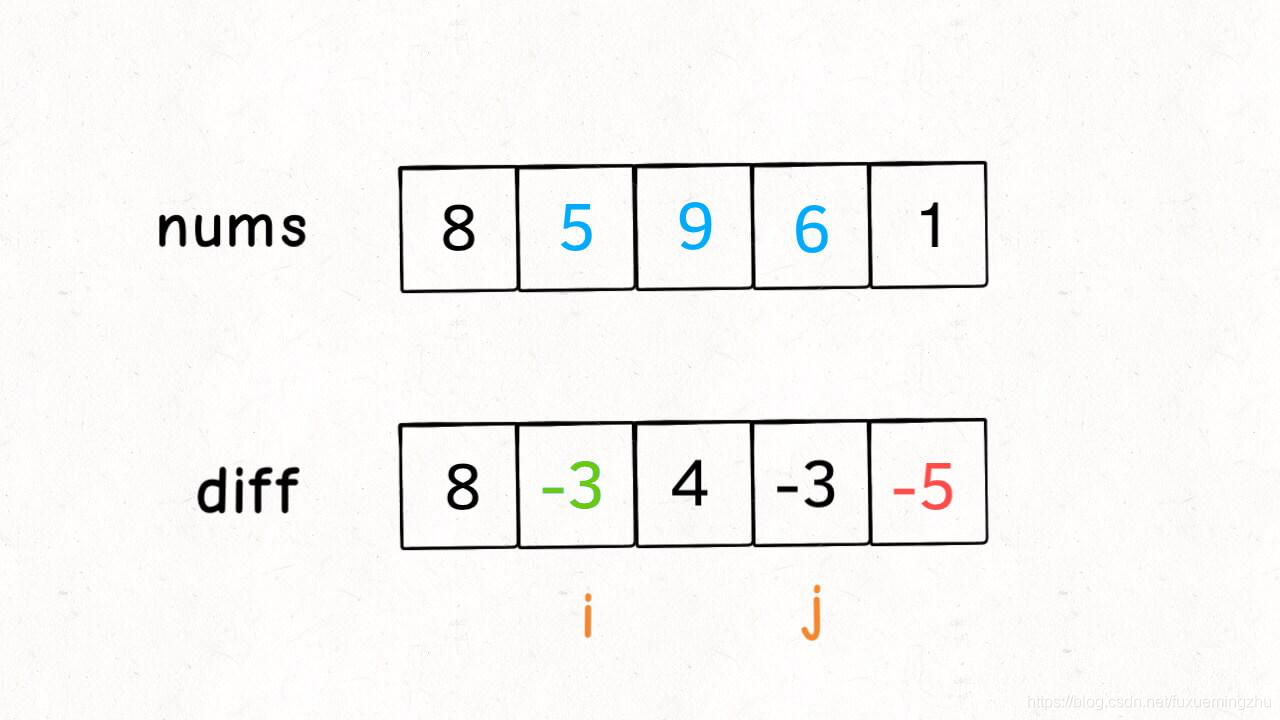
那么查分数组能起到什么用呢?当我们把差分数组的
那如果题目给出的是个区间,表示把一个区间里面把所有位置都
比如,想给
对于本题,其实就是一个初始时全为 0 的
- 注意本题的区间相当于左闭右开:即上车点
$capacity[1]$ 位置需要加上$capacity[0]$ ,而下车点$capacity[1]$ 就需要减去$capacity[0]$ 。原因是「乘客会自觉遵守 “先下后上” 的良好素质」,所以到了下车点的时候,到站的乘客立马下去了,就不占用位置了。
最终,我们要判断的是:当还原每个点的人数的时候,需要保证此点的人数不会大于
在下面的代码中,我直接初始化了长度为 1010 的路径差分数组,是因为题目给出的数据在 1000 以内。
首先根据
road[trip[1]] += trip[0];即在trip[1]的位置上车trip[0]个人。road[trip[2]] -= trip[0];即在trip[2]的位置下车trip[0]个人。
在完成差分数组的初始化之后,需要还原每个位置的人数,即
当累加完了所有的位置,发现都每个位置的
C++ 代码如下:
class Solution {
public:
bool carPooling(vector<vector<int>>& trips, int capacity) {
vector<int> road(1010, 0);
for (vector<int>& trip : trips) {
road[trip[1]] += trip[0];
road[trip[2]] -= trip[0];
}
int cur = 0;
for (int i = 0; i < 1009; i ++) {
cur += road[i];
if (cur > capacity) {
return false;
}
}
return true;
}
};参考资料:https://www.yuque.com/docs/share/a07ed436-527b-478c-b3aa-bb72dae94f88
2021 年 8 月 21 日 —— 入职新公司了