-
Notifications
You must be signed in to change notification settings - Fork 290
/
Copy pathlsi.md
70 lines (34 loc) · 6.51 KB
/
lsi.md
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
# 潜在语义索引\(LSI\)
---
在文本挖掘中,主题模型是比较特殊的一块,它的思想不同于我们常用的机器学习算法,因此这里我们需要专门来总结文本主题模型的算法。本文关注于潜在语义索引算法\(LSI\)的原理。
# 1. 文本主题模型的问题特点
在数据分析中,我们经常会进行非监督学习的聚类算法,它可以对我们的特征数据进行非监督的聚类。而主题模型也是非监督的算法,目的是得到文本按照主题的概率分布。从这个方面来说,主题模型和普通的聚类算法非常的类似。但是两者其实还是有区别的。
聚类算法关注于从样本特征的相似度方面将数据聚类。比如通过数据样本之间的欧式距离,曼哈顿距离的大小聚类等。而主题模型,顾名思义,就是对文字中隐含主题的一种建模方法。比如从“人民的名义”和“达康书记”这两个词我们很容易发现对应的文本有很大的主题相关度,但是如果通过词特征来聚类的话则很难找出,因为聚类方法不能考虑到到隐含的主题这一块。
那么如何找到隐含的主题呢?这个一个大问题。常用的方法一般都是基于统计学的生成方法。即假设以一定的概率选择了一个主题,然后以一定的概率选择当前主题的词。最后这些词组成了我们当前的文本。所有词的统计概率分布可以从语料库获得,具体如何以“一定的概率选择”,这就是各种具体的主题模型算法的任务了。
当然还有一些不是基于统计的方法,比如我们下面讲到的LSI。
# 2. 潜在语义索引\(LSI\)概述
潜在语义索引\(Latent Semantic Indexing,以下简称LSI\),有的文章也叫Latent Semantic Analysis(LSA)。其实是一个东西,后面我们统称LSI,它是一种简单实用的主题模型。LSI是基于奇异值分解(SVD)的方法来得到文本的主题的。而SVD及其应用我们在前面的文章也多次讲到,比如:[奇异值分解\(SVD\)原理与在降维中的应用](/ml/clean-feature/svd.md)和[矩阵分解在协同过滤推荐算法中的应用](/ml/recommand/matrix-filter.md)。如果大家对SVD还不熟悉,建议复习[奇异值分解\(SVD\)原理与在降维中的应用](/ml/clean-feature/svd.md)后再读下面的内容。
这里我们简要回顾下SVD:对于一个$$m \times n$$的矩阵A,可以分解为下面三个矩阵:
$$A_{m \times n} = U_{m \times m}\Sigma_{m \times n} V^T_{n \times n}$$
有时为了降低矩阵的维度到k,SVD的分解可以近似的写为:
$$A_{m \times n} \approx U_{m \times k}\Sigma_{k \times k}V^T_{k \times n}$$
如果把上式用到我们的主题模型,则SVD可以这样解释:我们输入的有m个文本,每个文本有n个词。而$$A_{ij}$$则对应第i个文本的第j个词的特征值,这里最常用的是基于预处理后的标准化TF-IDF值。k是我们假设的主题数,一般要比文本数少。SVD分解后,$$U_{il}$$对应第i个文本和第l个主题的相关度。$$V_{jm}$$对应第j个词和第m个词义的相关度。$$\Sigma_{lm}$$对应第l个主题和第m个词义的相关度。
也可以反过来解释:我们输入的有m个词,对应n个文本。而$$A_{ij}$$则对应第i个词档的第j个文本的特征值,这里最常用的是基于预处理后的标准化TF-IDF值。k是我们假设的主题数,一般要比文本数少。SVD分解后,$$U_{il}$$对应第i个词和第l个词义的相关度。$$V_{jm}$$对应第j个文本和第m个主题的相关度。$$\Sigma_{lm}$$对应第l个词义和第m个主题的相关度。
这样我们通过一次SVD,就可以得到文档和主题的相关度,词和词义的相关度以及词义和主题的相关度。
# 3. LSI简单实例
这里举一个简单的LSI实例,假设我们有下面这个有10个词三个文本的词频TF对应矩阵如下:
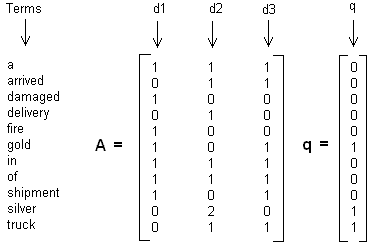
这里我们没有使用预处理,也没有使用TF-IDF,在实际应用中最好使用预处理后的TF-IDF值矩阵作为输入。
我们假定对应的主题数为2,则通过SVD降维后得到的三矩阵为:

从矩阵$$U_k$$我们可以看到词和词义之间的相关性。而从$$V_k$$可以看到3个文本和两个主题的相关性。大家可以看到里面有负数,所以这样得到的相关度比较难解释。
# 4. LSI用于文本相似度计算
在上面我们通过LSI得到的文本主题矩阵可以用于文本相似度计算。而计算方法一般是通过余弦相似度。比如对于上面的三文档两主题的例子。我们可以计算第一个文本和第二个文本的余弦相似度如下 :$$sim(d1,d2) = \frac{(-0.4945)*(-0.6458) + (0.6492)*(-0.7194)}{\sqrt{(-0.4945)^2+0.6492^2}\sqrt{(-0.6458)^2+(-0.7194)^2}}$$
# 5. LSI主题模型总结
LSI是最早出现的主题模型了,它的算法原理很简单,一次奇异值分解就可以得到主题模型,同时解决词义的问题,非常漂亮。但是LSI有很多不足,导致它在当前实际的主题模型中已基本不再使用。
主要的问题有:
1) SVD计算非常的耗时,尤其是我们的文本处理,词和文本数都是非常大的,对于这样的高维度矩阵做奇异值分解是非常难的。
2) 主题值的选取对结果的影响非常大,很难选择合适的k值。
3) LSI得到的不是一个概率模型,缺乏统计基础,结果难以直观的解释。
对于问题1),主题模型非负矩阵分解(NMF)可以解决矩阵分解的速度问题。对于问题2),这是老大难了,大部分主题模型的主题的个数选取一般都是凭经验的,较新的层次狄利克雷过程(HDP)可以自动选择主题个数。对于问题3),牛人们整出了pLSI\(也叫pLSA\)和隐含狄利克雷分布\(LDA\)这类基于概率分布的主题模型来替代基于矩阵分解的主题模型。
回到LSI本身,对于一些规模较小的问题,如果想快速粗粒度的找出一些主题分布的关系,则LSI是比较好的一个选择,其他时候,如果你需要使用主题模型,推荐使用LDA和HDP。