-
Notifications
You must be signed in to change notification settings - Fork 10
Introduction
Asami is a graph database, which may be a new approach to data management for some users. This page tries to explain what graph data is and how to use Asami to interact with it.
When we refer to a "Graph Database" we are not referring to the sort of graph that we often see in magazines, or are generated from spreadsheets. Instead, the "graph" being referenced here is a branch of mathematics called "Graph Theory". These graphs describe a set of items called "Nodes", which are connected with lines that are called "Edges".
An example of this might be a graph of social connections between people. The people in such a network can be represented by the "nodes" of a graph, and the "edges" can represent the social connections between them.

Each node appears once in a graph, regardless of how many connections it may have, and any pair of nodes will only have a single edge between them. Another important thing is that an image of a graph is merely a representation of the data. The location of the nodes and the edges do not matter. Also, edges do not interact in any way, so even if the lines indicating edges cross over each other, this does not mean anything. For instance, the following 2 graphs represent identical data to the above graph:
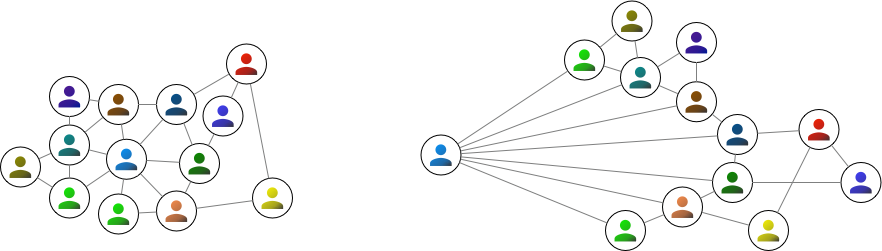
While many subtleties emerge from this structure, these simple ideas describe the entire foundation of this branch of mathematics!
However, most graph databases (including Asami) add two important features to the above definition: directed edges, and labeling.
A variation on the above graphs is when the edges are given a direction. We can represent this in an image using arrows instead of simple lines. Perhaps this might be used to represent a company hierarchy.
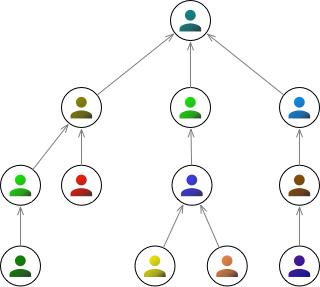
Importantly, having direction on edges means that there can now exist 2 edges between a pair of nodes: one in either direction.
A labeled graph will have labels on both the nodes and the edges. This provides a lot of new possibilities:
- Nodes need not represent the same types of things. They can represent anything: people, organizations, inventory items, account entries – anything at all.
- Multiple edges can connect the same nodes. For instance, a woman who is a mother to someone is also that person's parent. Both of these connections can be represented as distinct labeled edges.
Labeling some of the previous graph, we could get something like this:
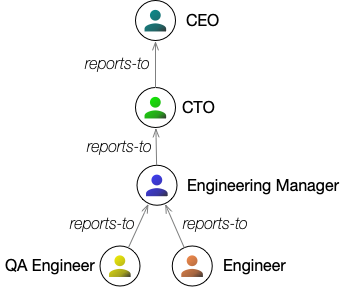
Labeled, directed graphs form the basic structure of graph databases.
Different graph databases make different choices about how they store their graph information. A common approach is for each node in the graph to be an object that has multiple attributes on it. We see this sort of thing in the Neo4J Graph Database.
Using this approach, let's add some details to the organization chart we had a moment ago.
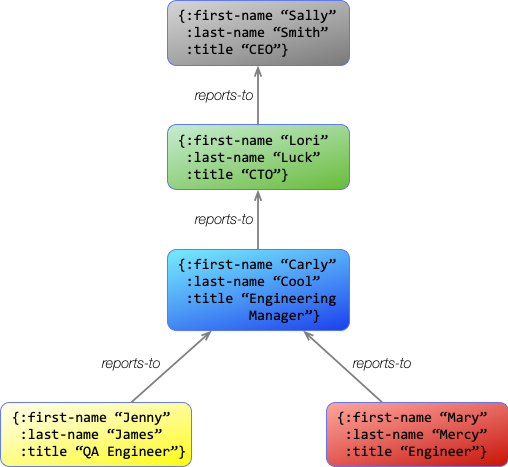
This diagram shows how entities can group a lot of information together in the graph. However, Asami and other graph databases actually break this information down into a basic graph structure. The information is identical, but it just gets managed a little differently.
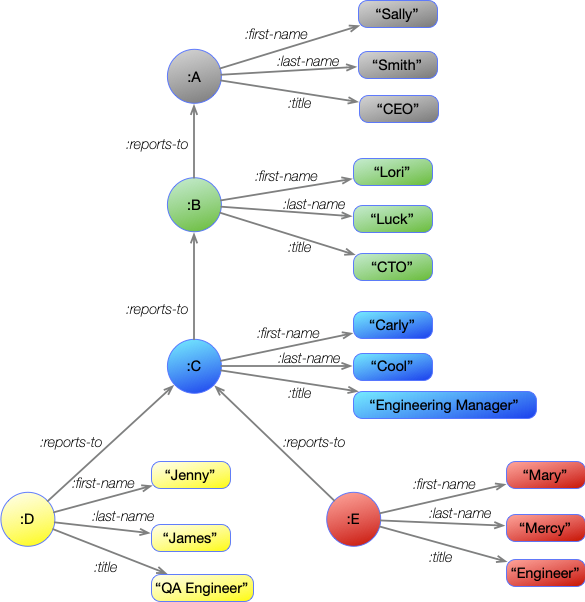
This is identical information as in the previous diagram, but instead of nodes being associated with complex data structures, every node represents only a single unit of information. Some are strings, while others provide a point to represent a group of information. These other nodes also need labels, so they have each been assigned a letter.
While the graph images above are clear in their structure, they have several limitations. As the amount of information expands, the size of the graph can grow significantly. The details and labels can get lost. For instance, there is no way to provide labels in the following graph without the image becoming enormous.
At the same time, the graph information has to be stored in a computer where it can be accessed in an efficient manner. This is done by storing only the information necessary for the graph.
The representation for basic graph information is a representation of the 3 elements of an edge:
start-node → edge → end-node
These elements form a single statement, or triple. For instance, the edge:
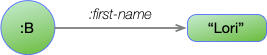
Is represented with the statement:
B first-name "Lori"
A group of statements like this provides the complete description for a graph. Using this we can represent the entire Organization Chart from above with the following statements:
| Graph Statements |
|---|
| A first-name "Sally" |
| A last-name "Smith" |
| A title "CEO" |
| B reports-to A |
| B first-name "Lori" |
| B last-name "Luck" |
| B title "CTO" |
| C reports-to B |
| C first-name "Carly" |
| C last-name "Cool" |
| C title "Engineering Manager" |
| D reports-to C |
| D first-name "Jenny" |
| D last-name "James" |
| D title "QA Engineer" |
| E reports-to C |
| E first-name "Mary" |
| E last-name "Mercy" |
| E title "Engineer" |
If we use this information to build a picture, we can reconstruct the original graph image or something very close. Remember that it doesn't matter how a graph image is laid out, so long as it has all of the correct nodes and edges.
The information here is very dense, but it is ideal for computers. It also follows a simple pattern that we can use when accessing the data.
When we want to access data in a graph, we use an approach called a pattern.
A graph pattern looks like a triple, but with one or more of the elements not filled in. These spaces will be given a name called a variable. These variables will be used to access the data that we are looking for. Variables are represented as a name with a ? character at the front.
For instance, the following pattern looks for the first-name of node E. The variable in the pattern is ?n:
[ E first-name ?n ]
The pattern can be applied to the graph to find all the statements that match it, and will fill in the variables. In this case, the pattern matches the statement:
E first-name "Mary"
So the variable ?n will be made equal to "Mary".
Most of the time a pattern will have multiple statements that it will match. In this case, the match will be a series of values for the variables in the pattern. To see this, let's look for all of the titles in the graph:
[?node title ?t]
This matches a series of statements:
A title "CEO"
B title "CTO"
C title "Engineering Manager"
D title "QA Engineer"
E title "Engineer"
The series leads to a series of values for ?node and ?t:
?node=A ?t="CEO"
?node=B ?t="CTO"
?node=C ?t="Engineering Manager"
?node=D ?t="QA Engineer"
?node=E ?t="Engineer"
The variables in each of these values are connected, so when ?node is A then ?t is "CEO", and when ?node is B then ?t is "CTO". We call each of these variable/value groups a binding. Within a binding, each variable is bound. So in the first binding the ?node is bound to A and the ?t is bound to "CEO". In the last binding the ?node is bound to E and the ?t is bound to "Engineer".
The result of matching a pattern to a graph is a set of bindings. In this case, the set of bindings is 5 long.
In fact, whenever a pattern returns only a single result, like in the previous section, it will also be a set of bindings. But as we saw, that set was only one binding long.