写一个查找一组字符串中的最长公共前缀字符串的函数
输入: ["flower","flow","flight"]
输出: "fl"
输入: ["dog","racecar","car"]
输出: ""
说明: 在输入的字符串中没有公共前缀
所有给定的输入只包含小写字母 a-z
一开始, 我们将描述一个简单的方法去找到一组字符串共享的最长前缀
采用这种想法, 算法会迭代遍历字符串 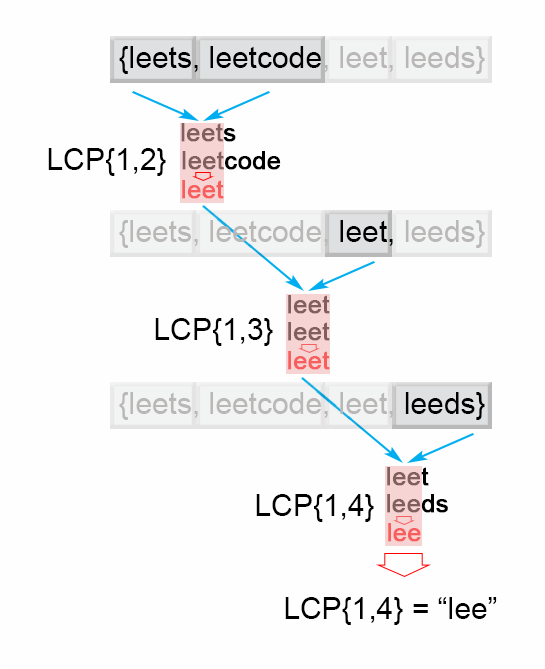
public String longestCommonPrefix(String[] strs) {
if (strs.length == 0) return "";
String prefix = strs[0];
for (int i = 1; i < strs.length; i++)
while (strs[i].indexOf(prefix) != 0) {
prefix = prefix.substring(0, prefix.length() - 1);
if (prefix.isEmpty()) return "";
}
return prefix;
}
- 时间复杂度:
$O(S)$ , S 是所有字符串中所有字符的个数之和 在最坏的情况下, 所有 n 个字符串相同; 算法比较 S1 和其他所有字符串 [S_2 ... S_n], 这将有 S 个字符比较, S 既是输入数组中所有字符之和 - 空间复杂度:
$O(1)$ , 我们仅使用常量个额外空间
假设一个非常段的字符串在数组尾; 以上方法将会做 S 次比较; 优化这中场景的办法是做垂直扫描; 在移动到下一列前, 我们从头到尾的比较在相同列上的字符 (字符串中相同的下标)
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0) return "";
for (int i = 0; i < strs[0].length() ; i++){
char c = strs[0].charAt(i);
for (int j = 1; j < strs.length; j ++) {
if (i == strs[j].length() || strs[j].charAt(i) != c)
return strs[0].substring(0, i);
}
}
return strs[0];
}
- 时间复杂度:
$O(S)$ , S 是所有字符串中所有字符的个数之和; 在最坏的情况将会是 m 长度的 n 个字符串, 并且算法执行 S = m * n 次字符比较; 尽管最坏的情况下和方法 1 是相同的时间复杂度, 但在最好的情况下至多 n * minLen 比较, minLen 是数组中最短字符串的长度 - 空间复杂度:
$O(1)$ , 我们仅使用常量个额外空间
这种算法的思想来源于结合 LCP 操作的属性; 我们注意到:
采用以上观察, 我们使用分而治之的技术, 这将会把 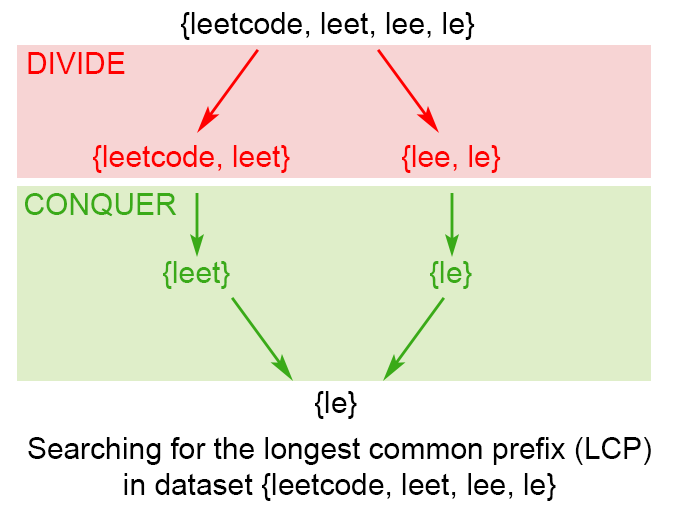
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0) return "";
return longestCommonPrefix(strs, 0 , strs.length - 1);
}
private String longestCommonPrefix(String[] strs, int l, int r) {
if (l == r) {
return strs[l];
}
else {
int mid = (l + r)/2;
String lcpLeft = longestCommonPrefix(strs, l , mid);
String lcpRight = longestCommonPrefix(strs, mid + 1,r);
return commonPrefix(lcpLeft, lcpRight);
}
}
String commonPrefix(String left,String right) {
int min = Math.min(left.length(), right.length());
for (int i = 0; i < min; i++) {
if ( left.charAt(i) != right.charAt(i) )
return left.substring(0, i);
}
return left.substring(0, min);
}
在最坏的情况下我们有 n 个相同的 m 长的字符
- 时间复杂度:
$O(S)$ , S 是所有字符串中所有字符的个数之和, S = m * n 时间复杂度是$2 * T(\frac {2} {n}) + O(m)$ ; 因此时间复杂度是$O(S)$ ; 在最好的情况下, 这个算法执行$O(minLen * n)$ 次比较, minLen 是数组中最短字符串的长度 - 空间复杂度:
$O(m * \log n)$ , 因为我们在执行栈中存储了递归调用, 可能会有内存溢出; 这里有$\log n$ 次递归调用, 每次存储需要 m 空间去保存结果, 所以空间复杂度是$O(m * \log n)$