README.md

2876. 有向图访问计数

English Version

题目描述

现有一个有向图，其中包含 n 个节点，节点编号从 0 到 n - 1 。此外，该图还包含了 n 条有向边。

给你一个下标从 0 开始的数组 edges ，其中 edges[i] 表示存在一条从节点 i 到节点 edges[i] 的边。

想象在图上发生以下过程：

• 你从节点 x 开始，通过边访问其他节点，直到你在 此过程 中再次访问到之前已经访问过的节点。

返回数组 answer 作为答案，其中 answer[i] 表示如果从节点 i 开始执行该过程，你可以访问到的不同节点数。

 

示例 1：

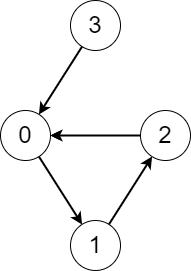
输入：edges = [1,2,0,0]
输出：[3,3,3,4]
解释：从每个节点开始执行该过程，记录如下：
- 从节点 0 开始，访问节点 0 -> 1 -> 2 -> 0 。访问的不同节点数是 3 。
- 从节点 1 开始，访问节点 1 -> 2 -> 0 -> 1 。访问的不同节点数是 3 。
- 从节点 2 开始，访问节点 2 -> 0 -> 1 -> 2 。访问的不同节点数是 3 。
- 从节点 3 开始，访问节点 3 -> 0 -> 1 -> 2 -> 0 。访问的不同节点数是 4 。

示例 2：

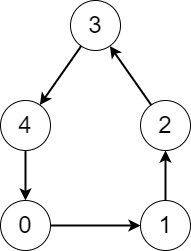
输入：edges = [1,2,3,4,0]
输出：[5,5,5,5,5]
解释：无论从哪个节点开始，在这个过程中，都可以访问到图中的每一个节点。

 

提示：

• n == edges.length
• 2 <= n <= 105
• 0 <= edges[i] <= n - 1
• edges[i] != i

解法

方法一：基环树 + 遍历搜索

我们可以用一个数组 $ans$ 记录每个节点的答案，用一个数组 $vis$ 记录每个节点的访问次序。

遍历每个节点 $i$，如果当前节点 $i$ 未被访问，我们就从节点 $i$ 开始遍历，此时有两种情况：

1. 如果遍历过程中，遇到了当前节点出发时走过的节点，那么此次遍历，一定是先走到了环内，然后沿着环走了一圈。对于环外的节点，其答案就是环的长度加上节点到环的距离；对于环内的节点，其答案就是环的长度。
2. 如果遍历过程中，遇到了此前节点出发时走过的节点，那么对于每个走过的节点，其答案就是当前节点到此节点的距离，加上此节点的答案。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是数组 $edges$ 的长度。

Python3

class Solution:
    def countVisitedNodes(self, edges: List[int]) -> List[int]:
        n = len(edges)
        ans = [0] * n
        vis = [0] * n
        for i in range(n):
            if not ans[i]:
                cnt, j = 0, i
                while not vis[j]:
                    cnt += 1
                    vis[j] = cnt
                    j = edges[j]
                cycle, total = 0, cnt + ans[j]
                if not ans[j]:
                    cycle = cnt - vis[j] + 1
                    total = cnt
                j = i
                while not ans[j]:
                    ans[j] = max(total, cycle)
                    total -= 1
                    j = edges[j]
        return ans

Java

class Solution {
    public int[] countVisitedNodes(List<Integer> edges) {
        int n = edges.size();
        int[] ans = new int[n];
        int[] vis = new int[n];
        for (int i = 0; i < n; ++i) {
            if (ans[i] == 0) {
                int cnt = 0, j = i;
                while (vis[j] == 0) {
                    vis[j] = ++cnt;
                    j = edges.get(j);
                }
                int cycle = 0, total = cnt + ans[j];
                if (ans[j] == 0) {
                    cycle = cnt - vis[j] + 1;
                }
                j = i;
                while (ans[j] == 0) {
                    ans[j] = Math.max(total--, cycle);
                    j = edges.get(j);
                }
            }
        }
        return ans;
    }
}

class Solution {
    void dfs(int curr, List<Integer> edges, int[] ans) {

        List<Integer> path = new ArrayList<>();
        int prev = -1;
        while (ans[curr] == 0) {
            path.add(curr);
            ans[curr] = prev == -1 ? -1 : ans[prev] - 1;
            prev = curr;
            curr = edges.get(curr);
        }
        int idx = path.size() - 1;
        if (ans[curr] < 0) {
            int cycle = ans[curr] - ans[path.get(idx)] + 1;
            int start = ans[curr];
            for (; idx >= 0 && ans[path.get(idx)] <= start; idx--) {
                ans[path.get(idx)] = cycle;
            }
        }
        for (; idx >= 0; idx--) {
            ans[path.get(idx)] = ans[edges.get(path.get(idx))] + 1;
        }
    }

    public int[] countVisitedNodes(List<Integer> edges) {
        int n = edges.size();
        int[] ans = new int[n];
        for (int i = 0; i < n; i++) {
            if (ans[i] > 0) {
                continue;
            }
            dfs(i, edges, ans);
        }
        return ans;
    }
}

C++

class Solution {
public:
    vector<int> countVisitedNodes(vector<int>& edges) {
        int n = edges.size();
        vector<int> ans(n), vis(n);
        for (int i = 0; i < n; ++i) {
            if (!ans[i]) {
                int cnt = 0, j = i;
                while (vis[j] == 0) {
                    vis[j] = ++cnt;
                    j = edges[j];
                }
                int cycle = 0, total = cnt + ans[j];
                if (ans[j] == 0) {
                    cycle = cnt - vis[j] + 1;
                }
                j = i;
                while (ans[j] == 0) {
                    ans[j] = max(total--, cycle);
                    j = edges[j];
                }
            }
        }
        return ans;
    }
};

Go

func countVisitedNodes(edges []int) []int {
	n := len(edges)
	ans := make([]int, n)
	vis := make([]int, n)
	for i := range ans {
		if ans[i] == 0 {
			cnt, j := 0, i
			for vis[j] == 0 {
				cnt++
				vis[j] = cnt
				j = edges[j]
			}
			cycle, total := 0, cnt+ans[j]
			if ans[j] == 0 {
				cycle = cnt - vis[j] + 1
			}
			j = i
			for ans[j] == 0 {
				ans[j] = max(total, cycle)
				total--
				j = edges[j]
			}
		}
	}
	return ans
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

TypeScript

function countVisitedNodes(edges: number[]): number[] {
    const n = edges.length;
    const ans: number[] = Array(n).fill(0);
    const vis: number[] = Array(n).fill(0);
    for (let i = 0; i < n; ++i) {
        if (ans[i] === 0) {
            let [cnt, j] = [0, i];
            while (vis[j] === 0) {
                vis[j] = ++cnt;
                j = edges[j];
            }
            let [cycle, total] = [0, cnt + ans[j]];
            if (ans[j] === 0) {
                cycle = cnt - vis[j] + 1;
            }
            j = i;
            while (ans[j] === 0) {
                ans[j] = Math.max(total--, cycle);
                j = edges[j];
            }
        }
    }
    return ans;
}

...