给你一棵 n 个节点的无向树,节点编号为 0 到 n - 1 。给你整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 有一条边。
同时给你一个下标从 0 开始长度为 n 的整数数组 values ,其中 values[i] 是第 i 个节点的 值 。再给你一个整数 k 。
你可以从树中删除一些边,也可以一条边也不删,得到若干连通块。一个 连通块的值 定义为连通块中所有节点值之和。如果所有连通块的值都可以被 k 整除,那么我们说这是一个 合法分割 。
请你返回所有合法分割中,连通块数目的最大值 。
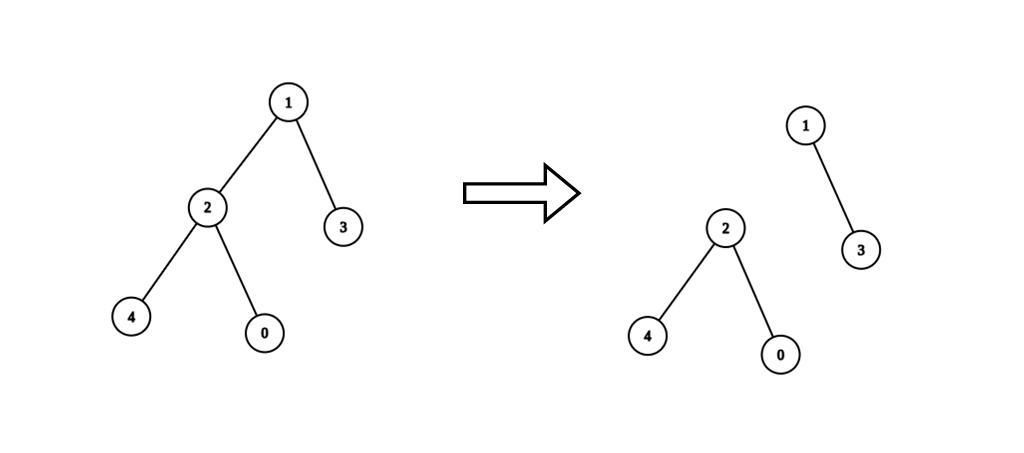
示例 1:
输入:n = 5, edges = [[0,2],[1,2],[1,3],[2,4]], values = [1,8,1,4,4], k = 6 输出:2 解释:我们删除节点 1 和 2 之间的边。这是一个合法分割,因为: - 节点 1 和 3 所在连通块的值为 values[1] + values[3] = 12 。 - 节点 0 ,2 和 4 所在连通块的值为 values[0] + values[2] + values[4] = 6 。 最多可以得到 2 个连通块的合法分割。
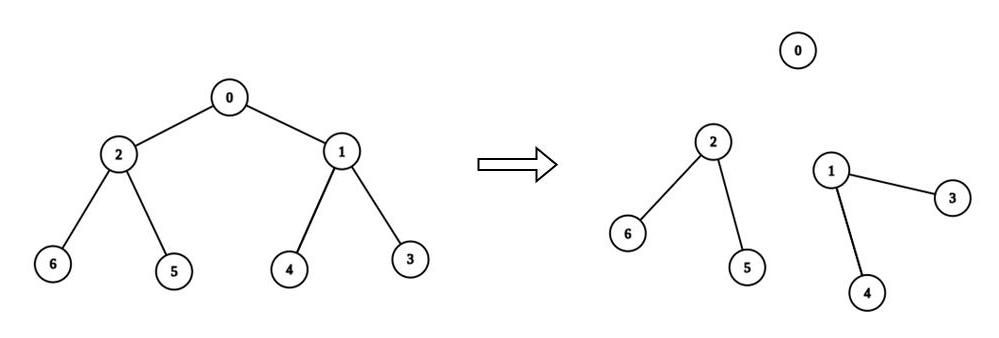
示例 2:
输入:n = 7, edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]], values = [3,0,6,1,5,2,1], k = 3 输出:3 解释:我们删除节点 0 和 2 ,以及节点 0 和 1 之间的边。这是一个合法分割,因为: - 节点 0 的连通块的值为 values[0] = 3 。 - 节点 2 ,5 和 6 所在连通块的值为 values[2] + values[5] + values[6] = 9 。 - 节点 1 ,3 和 4 的连通块的值为 values[1] + values[3] + values[4] = 6 。 最多可以得到 3 个连通块的合法分割。
提示:
1 <= n <= 3 * 104edges.length == n - 1edges[i].length == 20 <= ai, bi < nvalues.length == n0 <= values[i] <= 1091 <= k <= 109values之和可以被k整除。- 输入保证
edges是一棵无向树。
方法一:DFS
我们注意到,题目保证了整棵树的节点值之和可以被
因此,我们可以使用深度优先搜索的方法,从根节点开始遍历整棵树,对于每个节点,我们计算其子树中所有节点值之和,如果该和能被
时间复杂度
class Solution:
def maxKDivisibleComponents(
self, n: int, edges: List[List[int]], values: List[int], k: int
) -> int:
def dfs(i: int, fa: int) -> int:
s = values[i]
for j in g[i]:
if j != fa:
s += dfs(j, i)
nonlocal ans
ans += s % k == 0
return s
g = [[] for _ in range(n)]
for a, b in edges:
g[a].append(b)
g[b].append(a)
ans = 0
dfs(0, -1)
return ansclass Solution {
private int ans;
private List<Integer>[] g;
private int[] values;
private int k;
public int maxKDivisibleComponents(int n, int[][] edges, int[] values, int k) {
g = new List[n];
Arrays.setAll(g, i -> new ArrayList<>());
for (int[] e : edges) {
int a = e[0], b = e[1];
g[a].add(b);
g[b].add(a);
}
this.values = values;
this.k = k;
dfs(0, -1);
return ans;
}
private long dfs(int i, int fa) {
long s = values[i];
for (int j : g[i]) {
if (j != fa) {
s += dfs(j, i);
}
}
ans += s % k == 0 ? 1 : 0;
return s;
}
}class Solution {
int n, k;
int[] values;
int[] dfs(int curr, int parent, List<List<Integer>> adj) {
int[] res = new int[] {0, values[curr] % k};
for (int next : adj.get(curr)) {
if (next == parent) {
continue;
}
int[] update = dfs(next, curr, adj);
res[0] += update[0];
res[1] += update[1];
}
res[1] %= k;
res[0] += res[1] == 0 ? 1 : 0;
return res;
}
public int maxKDivisibleComponents(int n, int[][] edges, int[] values, int k) {
this.n = n;
this.k = k;
this.values = values;
List<List<Integer>> adj = new ArrayList<>();
int[][] dp = new int[n][2];
for (int i = 0; i < n; i++) {
adj.add(new ArrayList<>());
}
for (int[] edge : edges) {
adj.get(edge[0]).add(edge[1]);
adj.get(edge[1]).add(edge[0]);
}
int[] ans = dfs(0, -1, adj);
return ans[1] == 0 ? ans[0] : 0;
}
}class Solution {
public:
int maxKDivisibleComponents(int n, vector<vector<int>>& edges, vector<int>& values, int k) {
int ans = 0;
vector<int> g[n];
for (auto& e : edges) {
int a = e[0], b = e[1];
g[a].push_back(b);
g[b].push_back(a);
}
function<long long(int, int)> dfs = [&](int i, int fa) {
long long s = values[i];
for (int j : g[i]) {
if (j != fa) {
s += dfs(j, i);
}
}
ans += s % k == 0;
return s;
};
dfs(0, -1);
return ans;
}
};func maxKDivisibleComponents(n int, edges [][]int, values []int, k int) (ans int) {
g := make([][]int, n)
for _, e := range edges {
a, b := e[0], e[1]
g[a] = append(g[a], b)
g[b] = append(g[b], a)
}
var dfs func(int, int) int
dfs = func(i, fa int) int {
s := values[i]
for _, j := range g[i] {
if j != fa {
s += dfs(j, i)
}
}
if s%k == 0 {
ans++
}
return s
}
dfs(0, -1)
return
}function maxKDivisibleComponents(
n: number,
edges: number[][],
values: number[],
k: number,
): number {
const g: number[][] = Array.from({ length: n }, () => []);
for (const [a, b] of edges) {
g[a].push(b);
g[b].push(a);
}
let ans = 0;
const dfs = (i: number, fa: number): number => {
let s = values[i];
for (const j of g[i]) {
if (j !== fa) {
s += dfs(j, i);
}
}
if (s % k === 0) {
++ans;
}
return s;
};
dfs(0, -1);
return ans;
}