一个 n 个节点的无向树,节点编号为 0 到 n - 1 ,树的根结点是 0 号节点。给你一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] ,表示节点 ai 和 bi 在树中有一条边。
在每一个节点 i 处有一扇门。同时给你一个都是偶数的数组 amount ,其中 amount[i] 表示:
- 如果
amount[i]的值是负数,那么它表示打开节点i处门扣除的分数。 - 如果
amount[i]的值是正数,那么它表示打开节点i处门加上的分数。
游戏按照如下规则进行:
- 一开始,Alice 在节点
0处,Bob 在节点bob处。 - 每一秒钟,Alice 和 Bob 分别 移动到相邻的节点。Alice 朝着某个 叶子结点 移动,Bob 朝着节点
0移动。 - 对于他们之间路径上的 每一个 节点,Alice 和 Bob 要么打开门并扣分,要么打开门并加分。注意:
- 如果门 已经打开 (被另一个人打开),不会有额外加分也不会扣分。
- 如果 Alice 和 Bob 同时 到达一个节点,他们会共享这个节点的加分或者扣分。换言之,如果打开这扇门扣
c分,那么 Alice 和 Bob 分别扣c / 2分。如果这扇门的加分为c,那么他们分别加c / 2分。
- 如果 Alice 到达了一个叶子结点,她会停止移动。类似的,如果 Bob 到达了节点
0,他也会停止移动。注意这些事件互相 独立 ,不会影响另一方移动。
请你返回 Alice 朝最优叶子结点移动的 最大 净得分。
示例 1:
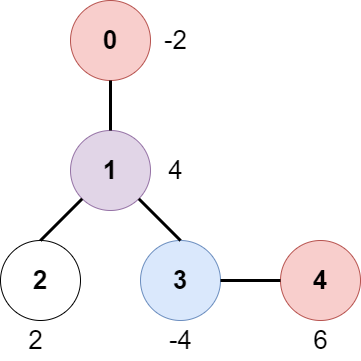
输入:edges = [[0,1],[1,2],[1,3],[3,4]], bob = 3, amount = [-2,4,2,-4,6] 输出:6 解释: 上图展示了输入给出的一棵树。游戏进行如下: - Alice 一开始在节点 0 处,Bob 在节点 3 处。他们分别打开所在节点的门。 Alice 得分为 -2 。 - Alice 和 Bob 都移动到节点 1 。 因为他们同时到达这个节点,他们一起打开门并平分得分。 Alice 的得分变为 -2 + (4 / 2) = 0 。 - Alice 移动到节点 3 。因为 Bob 已经打开了这扇门,Alice 得分不变。 Bob 移动到节点 0 ,并停止移动。 - Alice 移动到节点 4 并打开这个节点的门,她得分变为 0 + 6 = 6 。 现在,Alice 和 Bob 都不能进行任何移动了,所以游戏结束。 Alice 无法得到更高分数。
示例 2:
输入:edges = [[0,1]], bob = 1, amount = [-7280,2350] 输出:-7280 解释: Alice 按照路径 0->1 移动,同时 Bob 按照路径 1->0 移动。 所以 Alice 只打开节点 0 处的门,她的得分为 -7280 。
提示:
2 <= n <= 105edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedges表示一棵有效的树。1 <= bob < namount.length == namount[i]是范围[-104, 104]之间的一个 偶数 。
方法一:两次 DFS
根据题意,我们可以知道,Bob 的移动路径是固定的,即从节点
然后我们再跑一遍 DFS,求出 Alice 每条移动路径的最大得分,我们记 Alice 到达节点
- Alice 到达节点
$i$ 的时间$t$ 与 Bob 到达节点$i$ 的时间$ts[i]$ 相同,那么 Alice 和 Bob 同时打开节点$i$ 处的门,Alice 获得的分数为$v + \frac{amount[i]}{2}$ ; - Alice 到达节点
$i$ 的时间$t$ 小于 Bob 到达节点$i$ 的时间$ts[i]$ ,那么 Alice 打开节点$i$ 处的门,Alice 获得的分数为$v + amount[i]$ 。 - Alice 到达节点
$i$ 的时间$t$ 大于 Bob 到达节点$i$ 的时间$ts[i]$ ,那么 Alice 不打开节点$i$ 处的门,Alice 获得的分数为$v$ ,即不变。
当 Alice 到达叶子节点时,更新最大得分。
时间复杂度
class Solution:
def mostProfitablePath(
self, edges: List[List[int]], bob: int, amount: List[int]
) -> int:
def dfs1(i, fa, t):
if i == 0:
ts[i] = min(ts[i], t)
return True
for j in g[i]:
if j != fa and dfs1(j, i, t + 1):
ts[j] = min(ts[j], t + 1)
return True
return False
def dfs2(i, fa, t, v):
if t == ts[i]:
v += amount[i] // 2
elif t < ts[i]:
v += amount[i]
nonlocal ans
if len(g[i]) == 1 and g[i][0] == fa:
ans = max(ans, v)
return
for j in g[i]:
if j != fa:
dfs2(j, i, t + 1, v)
n = len(edges) + 1
g = defaultdict(list)
ts = [n] * n
for a, b in edges:
g[a].append(b)
g[b].append(a)
dfs1(bob, -1, 0)
ts[bob] = 0
ans = -inf
dfs2(0, -1, 0, 0)
return ansclass Solution {
private List<Integer>[] g;
private int[] amount;
private int[] ts;
private int ans = Integer.MIN_VALUE;
public int mostProfitablePath(int[][] edges, int bob, int[] amount) {
int n = edges.length + 1;
g = new List[n];
ts = new int[n];
this.amount = amount;
Arrays.setAll(g, k -> new ArrayList<>());
Arrays.fill(ts, n);
for (var e : edges) {
int a = e[0], b = e[1];
g[a].add(b);
g[b].add(a);
}
dfs1(bob, -1, 0);
ts[bob] = 0;
dfs2(0, -1, 0, 0);
return ans;
}
private boolean dfs1(int i, int fa, int t) {
if (i == 0) {
ts[i] = Math.min(ts[i], t);
return true;
}
for (int j : g[i]) {
if (j != fa && dfs1(j, i, t + 1)) {
ts[j] = Math.min(ts[j], t + 1);
return true;
}
}
return false;
}
private void dfs2(int i, int fa, int t, int v) {
if (t == ts[i]) {
v += amount[i] >> 1;
} else if (t < ts[i]) {
v += amount[i];
}
if (g[i].size() == 1 && g[i].get(0) == fa) {
ans = Math.max(ans, v);
return;
}
for (int j : g[i]) {
if (j != fa) {
dfs2(j, i, t + 1, v);
}
}
}
}class Solution {
public:
int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {
int n = edges.size() + 1;
vector<vector<int>> g(n);
for (auto& e : edges) {
int a = e[0], b = e[1];
g[a].emplace_back(b);
g[b].emplace_back(a);
}
vector<int> ts(n, n);
function<bool(int i, int fa, int t)> dfs1 = [&](int i, int fa, int t) -> bool {
if (i == 0) {
ts[i] = t;
return true;
}
for (int j : g[i]) {
if (j != fa && dfs1(j, i, t + 1)) {
ts[j] = min(ts[j], t + 1);
return true;
}
}
return false;
};
dfs1(bob, -1, 0);
ts[bob] = 0;
int ans = INT_MIN;
function<void(int i, int fa, int t, int v)> dfs2 = [&](int i, int fa, int t, int v) {
if (t == ts[i])
v += amount[i] >> 1;
else if (t < ts[i])
v += amount[i];
if (g[i].size() == 1 && g[i][0] == fa) {
ans = max(ans, v);
return;
}
for (int j : g[i])
if (j != fa) dfs2(j, i, t + 1, v);
};
dfs2(0, -1, 0, 0);
return ans;
}
};func mostProfitablePath(edges [][]int, bob int, amount []int) int {
n := len(edges) + 1
g := make([][]int, n)
for _, e := range edges {
a, b := e[0], e[1]
g[a] = append(g[a], b)
g[b] = append(g[b], a)
}
ts := make([]int, n)
for i := range ts {
ts[i] = n
}
var dfs1 func(int, int, int) bool
dfs1 = func(i, fa, t int) bool {
if i == 0 {
ts[i] = min(ts[i], t)
return true
}
for _, j := range g[i] {
if j != fa && dfs1(j, i, t+1) {
ts[j] = min(ts[j], t+1)
return true
}
}
return false
}
dfs1(bob, -1, 0)
ts[bob] = 0
ans := -0x3f3f3f3f
var dfs2 func(int, int, int, int)
dfs2 = func(i, fa, t, v int) {
if t == ts[i] {
v += amount[i] >> 1
} else if t < ts[i] {
v += amount[i]
}
if len(g[i]) == 1 && g[i][0] == fa {
ans = max(ans, v)
return
}
for _, j := range g[i] {
if j != fa {
dfs2(j, i, t+1, v)
}
}
}
dfs2(0, -1, 0, 0)
return ans
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
func max(a, b int) int {
if a > b {
return a
}
return b
}