给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,其中每个节点 至多 有一条出边。
图用一个大小为 n 下标从 0 开始的数组 edges 表示,节点 i 到节点 edges[i] 之间有一条有向边。如果节点 i 没有出边,那么 edges[i] == -1 。
请你返回图中的 最长 环,如果没有任何环,请返回 -1 。
一个环指的是起点和终点是 同一个 节点的路径。
示例 1:
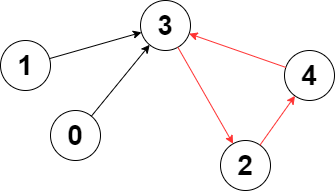
输入:edges = [3,3,4,2,3] 输出去:3 解释:图中的最长环是:2 -> 4 -> 3 -> 2 。 这个环的长度为 3 ,所以返回 3 。
示例 2:
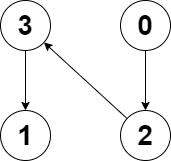
输入:edges = [2,-1,3,1] 输出:-1 解释:图中没有任何环。
提示:
n == edges.length2 <= n <= 105-1 <= edges[i] < nedges[i] != i
方法一:遍历出发点
我们可以遍历
时间复杂度
相似题目:2127. 参加会议的最多员工数
class Solution:
def longestCycle(self, edges: List[int]) -> int:
n = len(edges)
vis = [False] * n
ans = -1
for i in range(n):
if vis[i]:
continue
j = i
cycle = []
while j != -1 and not vis[j]:
vis[j] = True
cycle.append(j)
j = edges[j]
if j == -1:
continue
m = len(cycle)
k = next((k for k in range(m) if cycle[k] == j), inf)
ans = max(ans, m - k)
return ansclass Solution {
public int longestCycle(int[] edges) {
int n = edges.length;
boolean[] vis = new boolean[n];
int ans = -1;
for (int i = 0; i < n; ++i) {
if (vis[i]) {
continue;
}
int j = i;
List<Integer> cycle = new ArrayList<>();
for (; j != -1 && !vis[j]; j = edges[j]) {
vis[j] = true;
cycle.add(j);
}
if (j == -1) {
continue;
}
for (int k = 0; k < cycle.size(); ++k) {
if (cycle.get(k) == j) {
ans = Math.max(ans, cycle.size() - k);
break;
}
}
}
return ans;
}
}class Solution {
public:
int longestCycle(vector<int>& edges) {
int n = edges.size();
vector<bool> vis(n);
int ans = -1;
for (int i = 0; i < n; ++i) {
if (vis[i]) {
continue;
}
int j = i;
vector<int> cycle;
for (; j != -1 && !vis[j]; j = edges[j]) {
vis[j] = true;
cycle.push_back(j);
}
if (j == -1) {
continue;
}
for (int k = 0; k < cycle.size(); ++k) {
if (cycle[k] == j) {
ans = max(ans, (int) cycle.size() - k);
break;
}
}
}
return ans;
}
};func longestCycle(edges []int) int {
vis := make([]bool, len(edges))
ans := -1
for i := range edges {
if vis[i] {
continue
}
j := i
cycle := []int{}
for ; j != -1 && !vis[j]; j = edges[j] {
vis[j] = true
cycle = append(cycle, j)
}
if j == -1 {
continue
}
for k := range cycle {
if cycle[k] == j {
ans = max(ans, len(cycle)-k)
break
}
}
}
return ans
}
func max(a, b int) int {
if a > b {
return a
}
return b
}function longestCycle(edges: number[]): number {
const n = edges.length;
const vis = new Array(n).fill(false);
let ans = -1;
for (let i = 0; i < n; ++i) {
if (vis[i]) {
continue;
}
let j = i;
const cycle: number[] = [];
for (; j != -1 && !vis[j]; j = edges[j]) {
vis[j] = true;
cycle.push(j);
}
if (j == -1) {
continue;
}
for (let k = 0; k < cycle.length; ++k) {
if (cycle[k] == j) {
ans = Math.max(ans, cycle.length - k);
break;
}
}
}
return ans;
}