README.md

2133. 检查是否每一行每一列都包含全部整数

English Version

题目描述

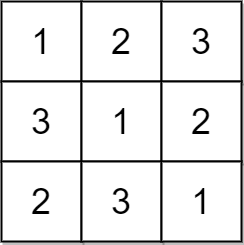
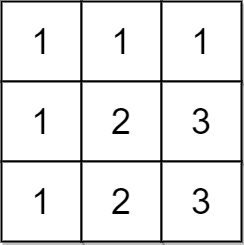
对一个大小为 n x n 的矩阵而言，如果其每一行和每一列都包含从 1 到 n 的 全部 整数（含 1 和 n），则认为该矩阵是一个 有效 矩阵。

给你一个大小为 n x n 的整数矩阵 matrix ，请你判断矩阵是否为一个有效矩阵：如果是，返回 true ；否则，返回 false 。

 

示例 1：

输入：matrix = [[1,2,3],[3,1,2],[2,3,1]]
输出：true
解释：在此例中，n = 3 ，每一行和每一列都包含数字 1、2、3 。
因此，返回 true 。

示例 2：

输入：matrix = [[1,1,1],[1,2,3],[1,2,3]]
输出：false
解释：在此例中，n = 3 ，但第一行和第一列不包含数字 2 和 3 。
因此，返回 false 。

 

提示：

• n == matrix.length == matrix[i].length
• 1 <= n <= 100
• 1 <= matrix[i][j] <= n

解法

Python3

class Solution:
    def checkValid(self, matrix: List[List[int]]) -> bool:
        n = len(matrix)
        for i in range(n):
            seen = [False] * n
            for j in range(n):
                v = matrix[i][j] - 1
                if seen[v]:
                    return False
                seen[v] = True
        for j in range(n):
            seen = [False] * n
            for i in range(n):
                v = matrix[i][j] - 1
                if seen[v]:
                    return False
                seen[v] = True
        return True

Java

class Solution {
    public boolean checkValid(int[][] matrix) {
        int n = matrix.length;
        for (int i = 0; i < n; ++i) {
            boolean[] seen = new boolean[n];
            for (int j = 0; j < n; ++j) {
                int v = matrix[i][j] - 1;
                if (seen[v]) {
                    return false;
                }
                seen[v] = true;
            }
        }
        for (int j = 0; j < n; ++j) {
            boolean[] seen = new boolean[n];
            for (int i = 0; i < n; ++i) {
                int v = matrix[i][j] - 1;
                if (seen[v]) {
                    return false;
                }
                seen[v] = true;
            }
        }
        return true;
    }
}

TypeScript

function checkValid(matrix: number[][]): boolean {
    const n = matrix.length;
    let rows = Array.from({ length: n }, () => new Array(n).fill(false));
    let cols = Array.from({ length: n }, () => new Array(n).fill(false));
    for (let i = 0; i < n; i++) {
        for (let j = 0; j < n; j++) {
            let cur = matrix[i][j];
            if (rows[i][cur] || cols[j][cur]) return false;
            rows[i][cur] = true;
            cols[j][cur] = true;
        }
    }
    return true;
}

C++

class Solution {
public:
    bool checkValid(vector<vector<int>>& matrix) {
        int n = matrix.size();
        for (int i = 0; i < n; ++i) {
            vector<bool> seen(n);
            for (int j = 0; j < n; ++j) {
                int v = matrix[i][j] - 1;
                if (seen[v]) return false;
                seen[v] = true;
            }
        }
        for (int j = 0; j < n; ++j) {
            vector<bool> seen(n);
            for (int i = 0; i < n; ++i) {
                int v = matrix[i][j] - 1;
                if (seen[v]) return false;
                seen[v] = true;
            }
        }
        return true;
    }
};

Go

func checkValid(matrix [][]int) bool {
	n := len(matrix)
	for i := 0; i < n; i++ {
		seen := make([]bool, n)
		for j := 0; j < n; j++ {
			v := matrix[i][j] - 1
			if seen[v] {
				return false
			}
			seen[v] = true
		}
	}
	for j := 0; j < n; j++ {
		seen := make([]bool, n)
		for i := 0; i < n; i++ {
			v := matrix[i][j] - 1
			if seen[v] {
				return false
			}
			seen[v] = true
		}
	}
	return true
}

...