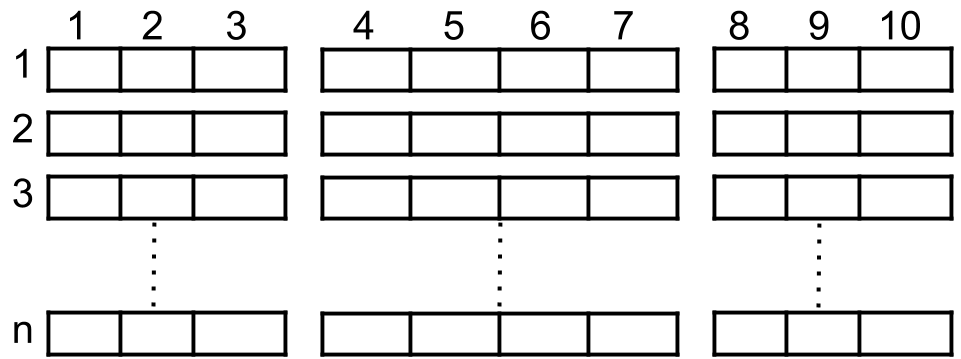
如上图所示,电影院的观影厅中有 n 行座位,行编号从 1 到 n ,且每一行内总共有 10 个座位,列编号从 1 到 10 。
给你数组 reservedSeats ,包含所有已经被预约了的座位。比如说,researvedSeats[i]=[3,8] ,它表示第 3 行第 8 个座位被预约了。
请你返回 最多能安排多少个 4 人家庭 。4 人家庭要占据 同一行内连续 的 4 个座位。隔着过道的座位(比方说 [3,3] 和 [3,4])不是连续的座位,但是如果你可以将 4 人家庭拆成过道两边各坐 2 人,这样子是允许的。
示例 1:
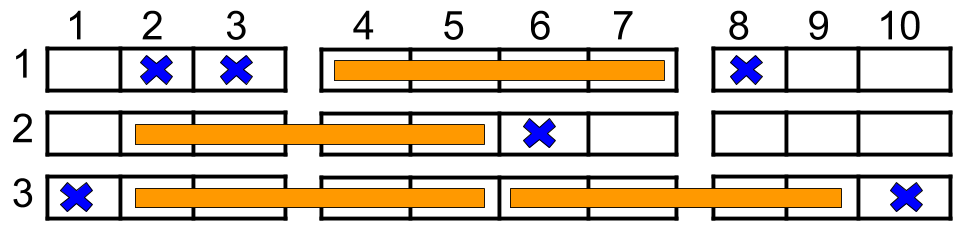
输入:n = 3, reservedSeats = [[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]] 输出:4 解释:上图所示是最优的安排方案,总共可以安排 4 个家庭。蓝色的叉表示被预约的座位,橙色的连续座位表示一个 4 人家庭。
示例 2:
输入:n = 2, reservedSeats = [[2,1],[1,8],[2,6]] 输出:2
示例 3:
输入:n = 4, reservedSeats = [[4,3],[1,4],[4,6],[1,7]] 输出:4
提示:
1 <= n <= 10^91 <= reservedSeats.length <= min(10*n, 10^4)reservedSeats[i].length == 21 <= reservedSeats[i][0] <= n1 <= reservedSeats[i][1] <= 10- 所有
reservedSeats[i]都是互不相同的。
方法一:哈希表 + 状态压缩
我们用哈希表
我们遍历
对于没有出现在哈希表
接下来,我们遍历哈希表中每一行的状态,对于每一行,我们依次尝试安排
遍历结束后,我们就得到了最终的答案。
时间复杂度
class Solution:
def maxNumberOfFamilies(self, n: int, reservedSeats: List[List[int]]) -> int:
d = defaultdict(int)
for i, j in reservedSeats:
d[i] |= 1 << (10 - j)
masks = (0b0111100000, 0b0000011110, 0b0001111000)
ans = (n - len(d)) * 2
for x in d.values():
for mask in masks:
if (x & mask) == 0:
x |= mask
ans += 1
return ansclass Solution {
public int maxNumberOfFamilies(int n, int[][] reservedSeats) {
Map<Integer, Integer> d = new HashMap<>();
for (var e : reservedSeats) {
int i = e[0], j = e[1];
d.merge(i, 1 << (10 - j), (x, y) -> x | y);
}
int[] masks = {0b0111100000, 0b0000011110, 0b0001111000};
int ans = (n - d.size()) * 2;
for (int x : d.values()) {
for (int mask : masks) {
if ((x & mask) == 0) {
x |= mask;
++ans;
}
}
}
return ans;
}
}class Solution {
public:
int maxNumberOfFamilies(int n, vector<vector<int>>& reservedSeats) {
unordered_map<int, int> d;
for (auto& e : reservedSeats) {
int i = e[0], j = e[1];
d[i] |= 1 << (10 - j);
}
int masks[3] = {0b0111100000, 0b0000011110, 0b0001111000};
int ans = (n - d.size()) * 2;
for (auto& [_, x] : d) {
for (int& mask : masks) {
if ((x & mask) == 0) {
x |= mask;
++ans;
}
}
}
return ans;
}
};func maxNumberOfFamilies(n int, reservedSeats [][]int) int {
d := map[int]int{}
for _, e := range reservedSeats {
i, j := e[0], e[1]
d[i] |= 1 << (10 - j)
}
ans := (n - len(d)) * 2
masks := [3]int{0b0111100000, 0b0000011110, 0b0001111000}
for _, x := range d {
for _, mask := range masks {
if x&mask == 0 {
x |= mask
ans++
}
}
}
return ans
}function maxNumberOfFamilies(n: number, reservedSeats: number[][]): number {
const d: Map<number, number> = new Map();
for (const [i, j] of reservedSeats) {
d.set(i, (d.get(i) ?? 0) | (1 << (10 - j)));
}
let ans = (n - d.size) << 1;
const masks = [0b0111100000, 0b0000011110, 0b0001111000];
for (let [_, x] of d) {
for (const mask of masks) {
if ((x & mask) === 0) {
x |= mask;
++ans;
}
}
}
return ans;
}